[백준] 1068번: 트리

https://www.acmicpc.net/problem/1068

initial

The very first thought was implemnting Node class of a binary tree until I realised this tree is not necessary a binary tree. Also, 0 is not necessarily the root node so we have to mark whichever node is marked as -1 as root node.

So I did a dfs way where I understood that for leaf node, graph[leaf_node]'s length would be 1 - its parent node. And when we meet a delete node, we dont recur beyond that node anymore. My approach works for around 70% of test cases

initial code

import math
from collections import defaultdict, deque
import sys
input = sys.stdin.readline

n=int(input())
lst = list(map(int,input().split()))
m=int(input())

graph=defaultdict(list)
count=0
visited=[False for _ in range(n)]
start=0
for i in range(len(lst)):
    if lst[i]==-1:
        start=i
        continue
    node=i
    par=lst[i]
    graph[node].append(par)
    graph[par].append(node)


def dfs(node):
    global count
    visited[node]=True
    if node==m:
        return
    if len(graph[node])==1:
        count+=1
        return
    for a in graph[node]:
        if not visited[a]:
            dfs(a)

dfs(start)
print(count)

wrong for this test case

But let's look at this test case:
7
3 6 6 -1 0 6 3
4

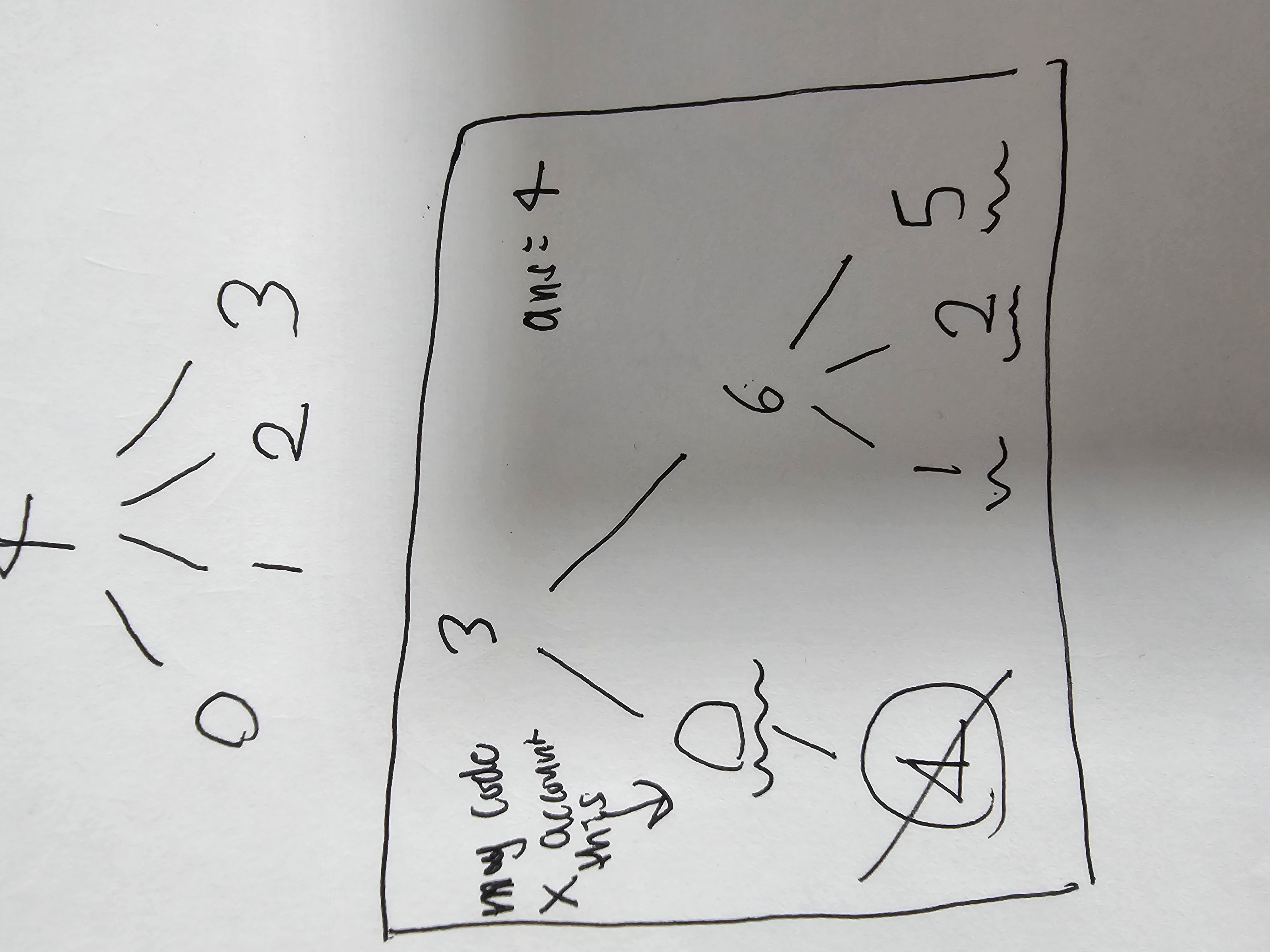
So we want to deleete node 4 but node 0 can be accounted as leaf. But the way I marked graph and the way that I made the logic that len(graph[node])==1 must be a leaft node is thus inaccurate.

So i tried fixing like this but other test cases are now wrong

for i in range(len(lst)):
    if lst[i]==-1:
        start=i
        continue
    node=i
    par=lst[i]
    if i==m:
        continue
    graph[node].append(par)
    graph[par].append(node)

solution

I googled and this way is quite clever.

We first mark the value within the list as -2 for a delete node. Then, we pass the delete node and the list to our dfs parameters. If any nodes have this delete node as its parent (i.e. lst[i]==delete_node) we do dfs on it by marking the node itself as -2 and so on if child nodes of that node have it as its parent.

Then, we have to iterate the lst one more time to see which are leaf nodes. The condition is
1) if its value is not marked as -2
2) if it is not parent of other nodes (i.e. i not in lst)

then we increment leaf count

import sys
input = sys.stdin.readline

n=int(input())
lst = list(map(int,input().split()))
m=int(input())
count=0

def dfs(delete,lst):
    lst[delete]=-2
    for i in range(n):
        if lst[i]==delete:
            dfs(i,lst)
dfs(m,lst)
for i in range(n):
    if lst[i]!=-2:
        if i!=-1 and i not in lst:
            count+=1
print(count)

easier solution (i think easier to understand)

this code is similar to mine.
there are mainly 2 diff

1) we only append the children to the graph[parent] so only unidirectional. This is related to how dfs works
2) very impt in the dfs, we pop all children of the delete node by iterating through all child node and putting that child node that as parameter to be popped. After all children has been dealt with, we append False to that parent node. (cuz the children will be popped anyway so there will be an empty list to get that False value) Later, when we iterate through graph, if it is not graph[i] (i.e. graph[i]=True) then it is leaf node.

n = int(input())
maps = list(map(int, input().split()))
delete = int(input())
# 노드의 개수와 각 노드의 부모 노드, 지울 노드를 입력받아줍니다.
graph = [[] for _ in range(n)]
for i in range(n):
    if maps[i] != -1:
        if i != delete:
            graph[maps[i]].append(i)
    # 부모가 -1인 경우 관계를 표시할 수 없고 지울 노드일 경우 다시 빼 줄 것이기
    # 때문에 모든 노드를 순서대로 확인하며 두 경우를 제외하고는 부모의 노드에 자식 노드를 표시해줍니다.
def dfs(a):
    while graph[a]:
        x = graph[a].pop()
        dfs(x)
        # 모든 자식 노드를 확인하고 가장 아래 노드부터 연결을 모두 끊은 뒤
    graph[a].append(False)
    # 삭제된 노드임을 표시하기 위해 False를 관계그래프에 넣어줍니다.
dfs(delete)
# 삭제할 노드를 기준으로 함수를 가동시켜줍니다.
cnt = 0
for i in range(n):
    if not graph[i]:
        cnt += 1
        # 모든 노드를 순회하며 자식 노드가 없는 경우를 확인하여줍니다.

print(cnt)

revisited jan 30th

that clever solution is clever. The approach is kinda like
https://velog.io/@whitehousechef/%EB%B0%B1%EC%A4%80-15900%EB%B2%88-%EB%82%98%EB%AC%B4-%ED%83%88%EC%B6%9C
where we do dfs from root to child node and spread the logic out.

that "easier" solution also works meh.

but both solutions runs the solution one more time after dfs to count the leaf nodes to handle that edge case above and count them accurately.

complexity

The provided code calculates the number of leaf nodes in a tree after removing a specified node. Here's the time and space complexity of the code:

Time Complexity:

• The dfs function performs a depth-first search, visiting each node and marking it as -2 if it should be removed. This operation takes O(n) time, where 'n' is the number of nodes in the tree.
• After that, there is another loop that iterates through the nodes to count leaf nodes. This loop also takes O(n) time, as it processes each node once.

So, the overall time complexity of the code is O(n), where 'n' is the number of nodes in the tree.

Space Complexity:

• The space complexity is determined by the call stack during the recursive DFS traversal. In the worst case, when the tree is a straight line (skewed tree), the space complexity can be O(n) because the call stack can grow as deep as 'n'.
• Additionally, the code uses a list (lst) to store the tree structure and a count variable. These data structures have space complexity O(n) as well.

So, the overall space complexity is O(n), dominated by the call stack and the data structures used in the code.