[백준] 12891번: DNA 비밀번호

https://www.acmicpc.net/problem/12891

initial

I used .count(), which is O(n) method to calculate each a,c,g,t for each sliding window iteration. This is time inefficient.

I also converted the dna "cgatgaa" to "124421" numerical format but actually that doesnt change anything cuz count will work for both cases.

runtime error solution

n,k = map(int,input().split())
dna = str(input())
dna_lst = []
lst = list(map(int, input().split()))
a,c,g,t = lst[0],lst[1],lst[2],lst[3]
dic = {"A":1, "C":2, "G":3, "T":4}
count =0
for d in dna:
    dna_lst.append(dic[d])
for i in range(len(dna_lst)-k+1):
    window = dna_lst[i:i+k]
    cntA, cntC, cntG, cntT = window.count(1), window.count(2), window.count(3), window.count(4)
    if cntA>=a and cntC >= c and cntG >= g and cntT >= t:
        count+=1
print(count)

solution

remember sliding window is subtracting the leftmost element and adding the rightmost element.

There are 2 ways for sliding window, initialise sliding window is a must for both ways but whether you account that initialised sliding window before your main logic or within your main logic is your choice. The latter would be cleaner and to do so, you have to adjust your main logic which is a bit harder.

sliding window accounted before main logic

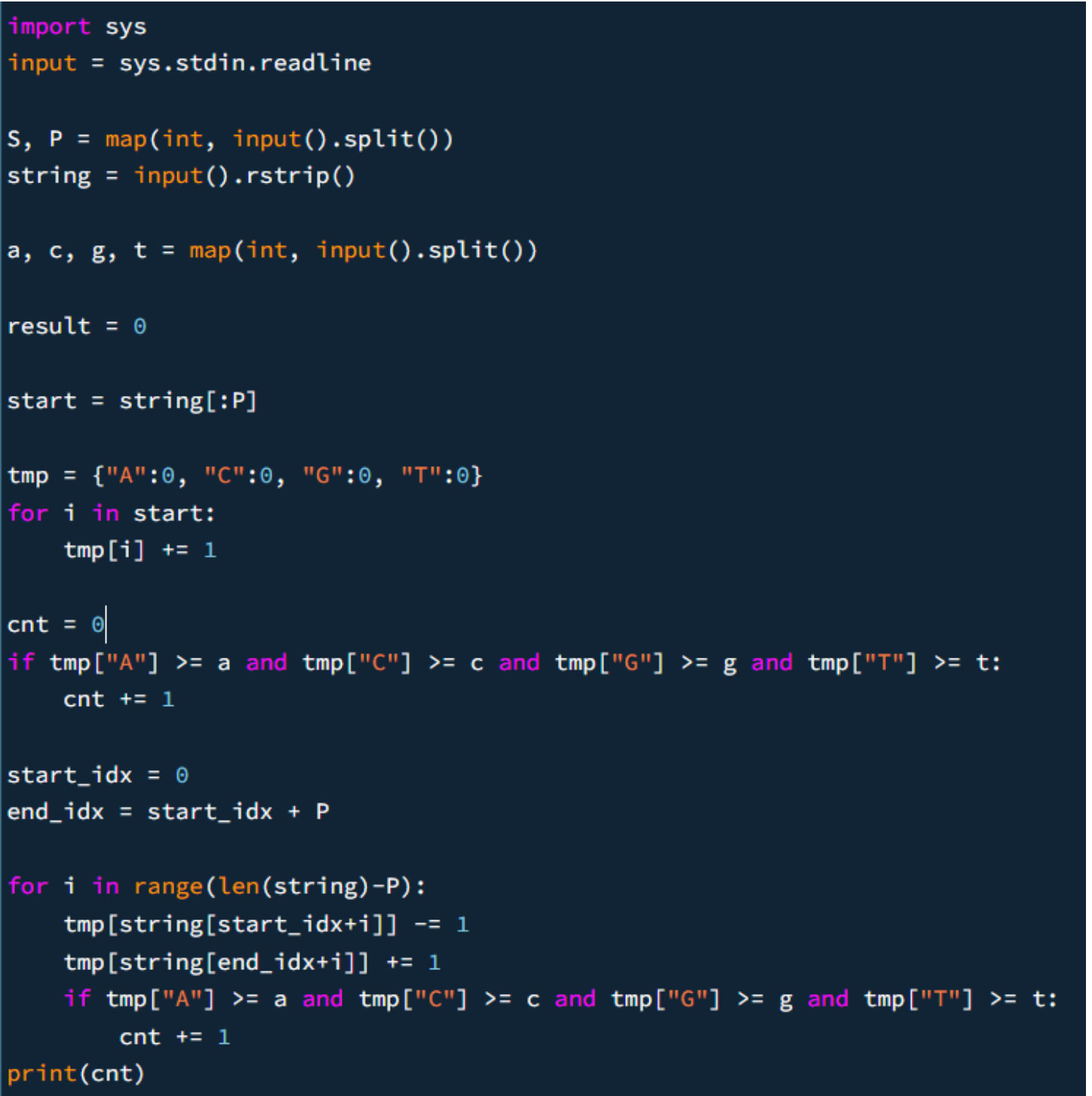
before the for loop main logic, we accounted for the initalised sliding window by incrementing count if we meet the condition.

sliding window accounted in main logic

This is cleaner but harder. How do we do this?

The way we initialise the sliding window is different.
window = dna[:k-1]. Notice the k-1. This is an incomplete sliding window, which will be filled up in the main for loop logic.

n,k = map(int,input().split())
dna = str(input())
a,c,g,t= map(int, input().split())
dic = {"A":0, "C":0, "G":0, "T":0}
# incomplete sliding window with the rightmost element not accounted for
# to fit in logic instead of calculating for initial window separately
window = dna[:k-1]
count =0
for i in window:
    dic[i]+=1
left,right = 0,k-1

for i in range(len(dna)-k+1):
    dic[dna[right]]+=1
    if dic['A']>=a and dic['C']>=c and dic['G']>=g and dic['T']>=t:
        count+=1
    dic[dna[left]]-=1
    left+=1
    right+=1
print(count)

So this main for loop logic works on incomplete sliding window that is missing the rightmost value at the start.

you can use while loop (while right < s) instead of for loop like

from collections import deque

s, p = map(int, input().split())
string = list(str(input()))
A, C, G, T = map(int, input().split())

dic = {'A': 0, 'C': 0, 'G': 0, 'T': 0}
left, right = 0, p-1
arr = deque(string[left:right])
for i in arr:
    dic[i] += 1
cnt = 0

while right < s:

    # 구간 완성
    dic[string[right]] += 1 # 가장 오른쪽 원소 추가

    # 계산
    if dic['A'] >= A  and dic['C'] >= C and dic['G'] >= G and dic['T'] >= T:
        cnt += 1

    # 구간이동
    dic[string[left]] -= 1 # 가장 왼쪽 원소 제거
    left += 1
    right += 1

print(cnt)

complexity

The code you provided seems to be an implementation of a sliding window approach to count the number of substrings of length k within a given DNA sequence (dna) that contain at least a 'A's, c 'C's, g 'G's, and t 'T's. Here's the complexity analysis of the code:

1. Initialization (Constant Time):

   • Reading n and k and creating the dna string take constant time.

2. Initialization of dic (Constant Time):

   • Creating the dictionary dic with four keys ('A', 'C', 'G', 'T') and initializing their values to 0 takes constant time since there are only four keys.

3. Sliding Window (Linear Time):

   • The code uses a sliding window approach to scan through the DNA sequence. It maintains a window of size k and slides it through the sequence.
   • The loop iterates len(dna) - k + 1 times, where len(dna) is the length of the DNA sequence. For each iteration, it updates the dic dictionary and checks if the conditions dic['A'] >= a, dic['C'] >= c, dic['G'] >= g, and dic['T'] >= t are met.
   • Since each iteration of the loop involves constant time operations (updating the dictionary and checking conditions), and there are len(dna) - k + 1 iterations, the time complexity of the sliding window part is O(len(dna)).

4. Printing (Constant Time):

   • Printing the final count takes constant time.

Overall, the time complexity of the code is dominated by the sliding window part, which is O(len(dna)). The space complexity is also O(1) because the size of the dic dictionary remains constant regardless of the input size.

In summary, the code efficiently counts the number of substrings meeting specific conditions using a sliding window approach with a time complexity of O(len(dna)).