[백준] 1655번: 가운데를 말해요

https://www.acmicpc.net/problem/1655

initial

I did an exact same question on leetcode where it is using max and min heap to find the median value. But I forgot :<

solution

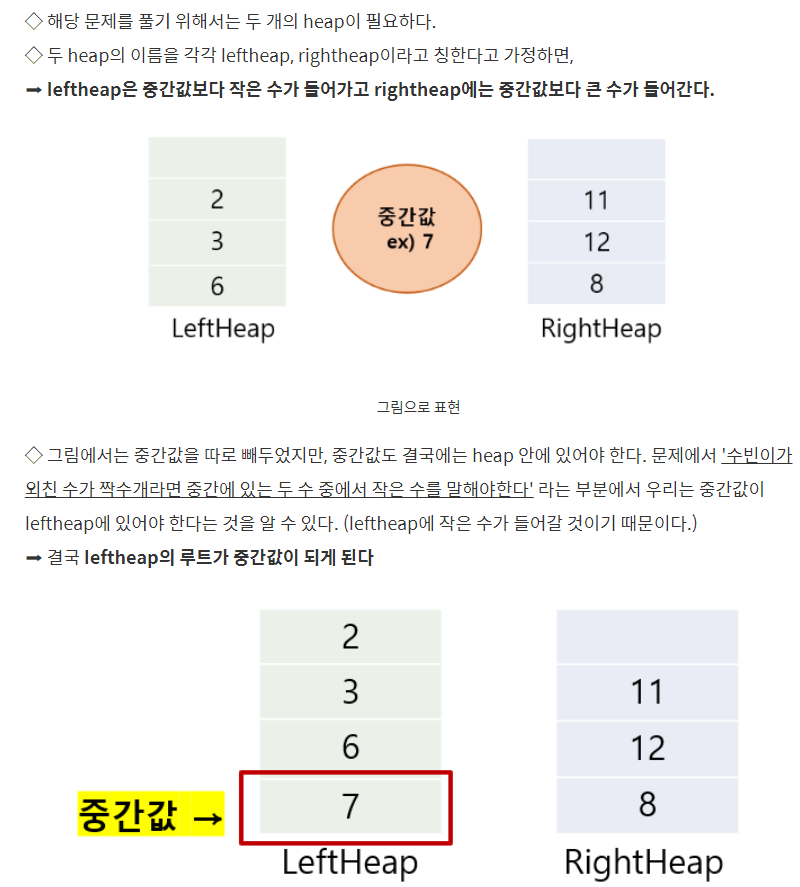
ref: https://art-coding3.tistory.com/44

So our max heap/leaf heap will be storing the lower smaller half while right heap/min heap will be storing the higher half. Root of lower half in left heap will be the largest in that heap while root of upper half in right heap will be the smallest in the heap. Very importantly, the median value has to be stored somewhere, so we are gonna put it in leftheap/max heap.

One tricky bit is so we are gonna put number in left heap (max heap) by (-number) be careful with the minus for max heap and fill right heap and fill left heap and fill right heap and so on. But what if root stored in left heap is bigger than root in right heap? Then our left heap is no longer storing the lower half of our number list so we need to pop it and push it to the right heap. Similiarly we pop the root of right heap and push it to left heap.

correct:

import heapq
import sys

input = sys.stdin.readline
n= int(input())

max_heap = []
min_heap = []
heapq.heapify(max_heap)
heapq.heapify(min_heap)
# max heap stores smaller half and the median value itself, min heap stores bigger half
for _ in range(n):
    i = int(input())
    if len(max_heap)==len(min_heap):
        heapq.heappush(max_heap,-i)
    else:
        heapq.heappush(min_heap, i)
    
    if max_heap and min_heap and -max_heap[0]>min_heap[0]:
        big = heapq.heappop(max_heap)
        small = heapq.heappop(min_heap)
        heapq.heappush(min_heap,-big)
        heapq.heappush(max_heap,-small)
    print(-max_heap[0])

revisited jan 15th

So i knew its using 2 heaps like trying to create a queue from 2 stacks. But I wasnt sure what logic to put incoming elements. Do I just sequentially put number one in max_heap, two in min_heap, three in max_heap and so on like that? (YES) That is cuz median is literally the middle value so we have to input values like that one by one into the 2 heaps.

The impt thing is we need to set where the median is gonna be placed cuz it has to exist somewhere either in max_heap or min_heap. In this case, we chose the max_heap. So if we have decided that way, the first element needs to come in to max_heap (cuz median of length 1 list is just itself). Then, the second element comes into min_heap. And third element comes in to max_heap and so on.

BUT it is possible that bcos the input numbers are not sorted, like for example when -99 comes in, it is possible that the root of max heap is BIGGER than root of min heap . In any input numbers, if there is such case we have to reverse the 2 roots (cuz q asked to print the smaller value), as explained in initial explan. Just becareful of the - in max_heap value.

complexity

The given code efficiently calculates and maintains the median of a sequence of numbers as they are read. The time complexity of this algorithm is O(log n) for each insertion and retrieval operation. Let's break down the complexity:

1. Heap Operations:

   • Insertion (pushing onto a heap): O(log n)
   • Retrieval (accessing the heap's root element): O(1)

2. In each iteration, one number is inserted into either the max_heap or min_heap, followed by a comparison to rebalance the heaps if necessary. This comparison and rebalancing operation takes constant time, O(1).

3. Printing the median (accessing the root element of max_heap): O(1)

Since the most time-consuming operation is the insertion into the heap, and this operation occurs once per iteration, the overall time complexity is O(log n) per number read. This is efficient for maintaining the median as numbers are added.

The space complexity is O(n) because both max_heap and min_heap can store up to n/2 elements each, depending on the sequence of numbers.