< 수강분량 : 기초수학(1~7), 파이썬 기초문풀(1~3) >
✅ 약수와 소수
- 약수 : 어떤 수를 나누어 떨어지게 하는 수
- 소수 : 1과 자신만을 약수로 가지는 수 <-> 합성수
(*단, 1은 소수도 합성수도 아님)
✅ 소인수와 소인수분해
- 소인수 : 약수(인수) 중에서 소수인 숫자
- 소인수분해 : 1보다 큰 정수를 소인수의 곱으로 나타낸 것.
소인수분해를 통해 약수를 정확하고 쉽게 구할 수 있음.
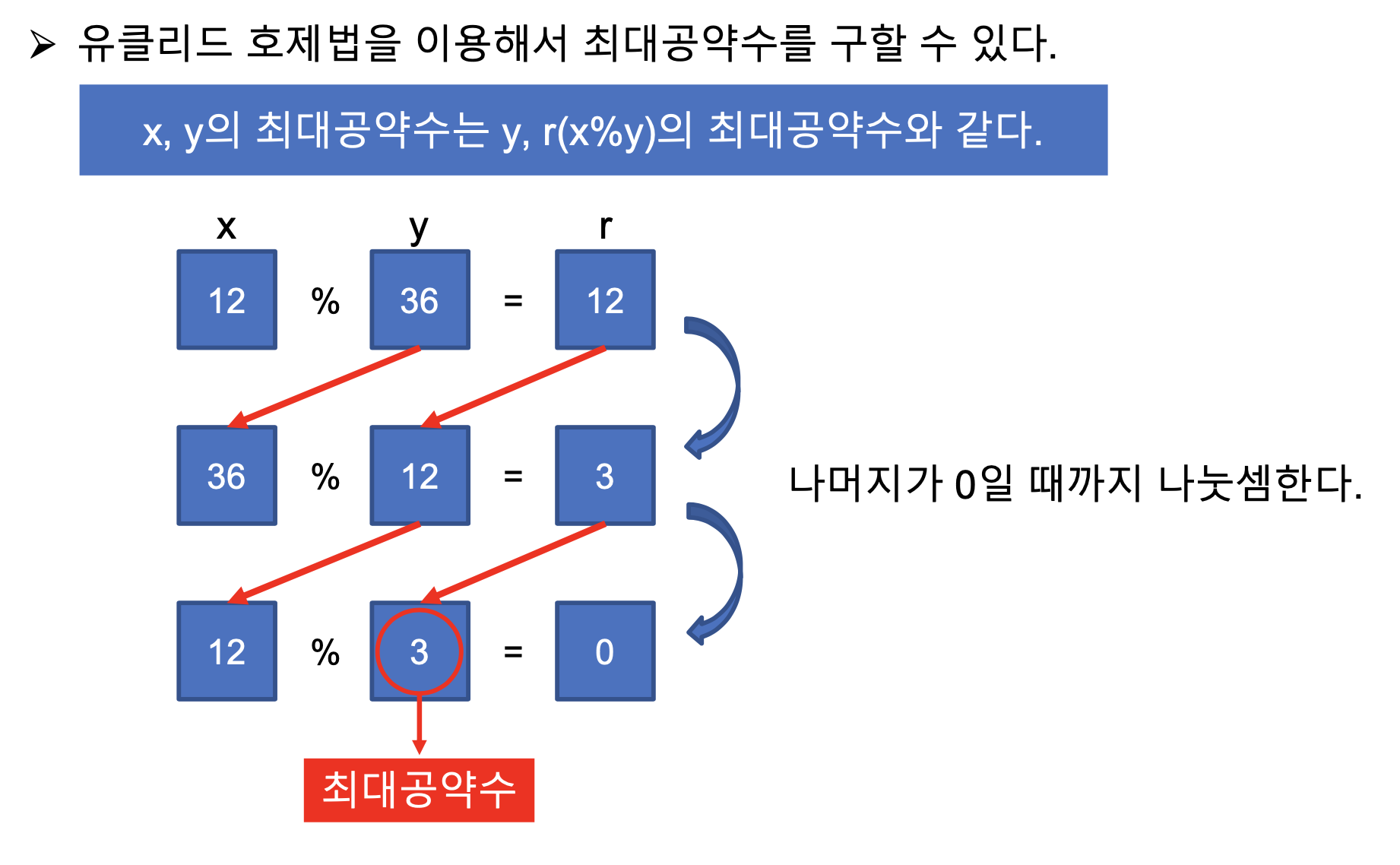
✅ 공약수와 최대공약수
- 공약수 : 두 개 이상의 수에서 공통된 약수 (1 포함)
(*공약수가 1뿐이라면 서로소라고 칭함) - 최대공약수 : 1보다 큰 정수를 소인수의 곱으로 나타낸 것.
공약수는 최대공약수의 약수임.
✅ 공배수와 최소공배수
- 공배수 : 두 개 이상의 수에서 공통된 배수
- 최소공배수 : 공배수 중 가장 작은 수.
소인수분해를 이용하면 최소공배수 및 공배수를 구할 수 있다.
두 수의 곱 // 최대공약수 = 최소공배수
✅ 진법
- 진법 : 특정 숫자 몇 개를 사용하여 수를 표시하는 방법이다.
1) 2진수로 변환(binary) : bin() / format(dNum, #b)
2) 8진수로 변환(octal) : oct() / format(dNum, #o)
3) 16진수로 변환(Hexadecimal) : hex() / format(dNum, #x)
(*1), 2), 3)의 변환 결과는 문자열이다!)
4) 10진수로 변환 : int() / int(dNum, 2/8/16)
✅ 수열
- 수열 : 규칙성을 가지고 나열되어 있는 수들
- an = Sn - S(n-1) (단, n>=2, a1 = S1)
- 등차수열 : 연속된 두 항의 차이가 일정한 수열
- an = a1 + ((n-1) d)
- Sn = n (a1 + an) / 2
- 등차중항 : 연속된 세항에서 가운데 항
- an = (a(n-1) + a(n+1)) / 2
- 등비수열 : 연속된 두 항의 비가 일정한 수열
- an = a1 r^(n-1)
- Sn = a1 (1-(r^n)) / (1-r)
- 등비중항 : 연속된 세항에서 가운데 항
- an^2 = a(n-1) * a(n+1)
- 시그마 : 수열의 합을 나타내는 기호 (Σ)
- 계차수열 : 어떤 수열의 인접하는 두 항의 차로 이루어진 수열
- b1 = a2 - a1; b(n-1) = an - a(n-1) - 피보나치수열 : 세번째 항은 두번째 항과 첫번째 항을 더한 합
- an = a(n-2) + a(n-1) (a1 = 1, a2=1 일 때)
- 팩토리얼 : 1부터 양의 정수 n까지의 정수를 모두 곱한 것
- 0! = 1
- 군수열 : 여러 개의 항을 묶었을 때 규칙성을 가지는 수열
- an = n; Sn = (n^2 + n) / 2
✅ 순열, 조합, 확률
-
순열(permutation) : n개에서 r개를 택하여 일렬로 나열하는 경우의 수
- nPr = n! / (n-r)!
- 원순열 : 시작과 끝의 구분이 없는 순열 (n!/n or (n-1)!)
-
조합(combination) : 순서 상관 없이 n개에서 r개를 택하는 경우의 수
- nCr = nPr / r! = n! / r! * (n-r)! -
확률 : 모든 사건에서 특정 사건이 일어날 수 있는 수를 나타낸 것
- 모든 사건 -> 표본공간 (sample)
- 특정 사건 -> 사건 (event)
- 조합을 이용해 확률을 알아낼 수 있다.
"이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다."
