알고리즘 코딩테스트 STUDY - 빅 오 표기법 (시간 복잡도, 공간복잡도)

빅 오 표기법

빅오 표기법은 알고리즘의 효율성을 표기해주는 표기법이다. 알고리즘의 효율성은 데이터 개수가 주어져있을때 덧셈, 뺄셈, 곱셈 같은 기본 연산의 횟수를 의미한다. 보통 알고리즘의 시간 복잡도(시간 효율성)와 공간 복잡도(메모리의 효율성)를 나타낼때 주로 사용된다.

시간 복잡도

예를들어, 1부터 n까지 전부 다 더한 값을 반환하는 코드를 쓸 때

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

라는 코드를 적을 수 있을 것이다. 하지만 이 코드를 이렇게 표현 할 수도 있을 것이다.

function addUpTo(n) {
  return n * (n + 1) / 2;
}

짧은 코드라고 해서 더 좋은 코드라고 보긴 어렵지만, 앞의 코드보다 조금 더 수학적이다.
앞의 코드랑 똑같이 작동하는걸 알 수 있다. 이 중에서 더 나은 코드는 뭘까?

어떤 코드가 더 빠른지? 작은 메모리로 할 수 있는지? 코드를 얼마나 쉽게 읽을 수 있을지?에 대해서 생각해봐야 할 것이다.

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}
 let t1 = performance.now();
 addUpto(1000000000);
 let t2 = performance.now();
 console.log(`Time Elapsed: ${(t2 - t1)} / 1000} seconsd.`) 

10억이라는 숫자를 처리 할 때 드는 시간을 계산해보자. 이 코드는 1.2575초 쯤 걸린다.

function addUpTo(n) {
  return n * (n + 1) / 2;
}
 let t1 = performance.now();
 addUpto(1000000000);
 let t2 = performance.now();
 console.log(`Time Elapsed: ${(t2 - t1)} / 1000} seconsd.`) 

이 코드도 똑같이 10억이라는 숫자를 처리 할 때 드는 시간을 계산해보자. 첫번째 코드보다 훨씬 오래 걸리는 초가 나온다.

더 짧은 코드지만 더 긴 코드보다 더 처리 시간이 오래걸린다는 걸 알 수 있다.
짧다고 해서 가장 좋은 코드는 아니라는 것이다. 이렇게 "시간의 문제"가 있다.

하지만 시간으로 측정하기에는 브라우저에서 뭘 켜놨는지 그 기계의 성능의 차이도 있다.
그래서 무조건 빠르게 처리한다고해서 좋은 코드도 아니라는 것이다. 시간으로 비교하지않아도 비교 할 수 있는 방법이 있어야 한다. 이게 바로 빅 오 표기법이다.

코드가 실행될떄 걸리는 정확한 시간을 세는게 아니라 대신에 컴퓨터가 처리해야하는 연산의 개수를 세면 된다. 시간은 항상 연산의 개수에 달라질 것이다.

function addUpTo(n) {
  return n * (n + 1) / 2;
}

이 코드를 보면 곱하기 하나 더하기 하나 나누기 하나가 있다. 연산을 세번해야 하는 것이다. n의 크기가 작든 크든 말이다.

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;

이 코드를 보면 n의 개수만큼 더하기 연산자가 사용되고 =할당 연산자도 사용된다. 하지만 +=이것도 하나의 연산자이고 n의 개수가 커질수록 n의 값대로 한번씩 연산의 개수가 늘어난다. total = 0과 let i = 1은 한번만 이루어진다.

하지만 이렇게 연산자의 개수를 세는건 쉬운 일이 아니다. 정확한 숫자는 사실 상관이 없다. 전체적인 추세를 보는게 중요하다. 빅오를 볼 때 이런것에 집중할 것이다. n이 커질수록 연산의 갯수도 비례적으로 커진다는것에 포인트를 잡는 것이다.

이 두가지를 비교해봤을때,
두번째 코드는 n의수가 아무리 늘어나도 비슷한 초를 보여주지만 첫번째 코드는 n의 개수만큼 비례해서 커졌다.

빅 오는 정식으로 입력된 내용이 늘어날수록 알고리즘에 실행 시간이 어떻게 변하는지 설명하는 공식적인 방식이다. 빅 오는 어떤 펑션의 입력값이 늘어나는 것과 펑션 실행 시간이 변하는 것에대한 관계를 말한다. 오로지 전반적인 추세에 주목 하는 것이다.

n이 커질수록 실행 시간이 n의 제곱일수도 있고 영향을 받지않아 똑같을수도 있다. 실행 시간이 가질 수 있는 가장 높은 실행 값이다.

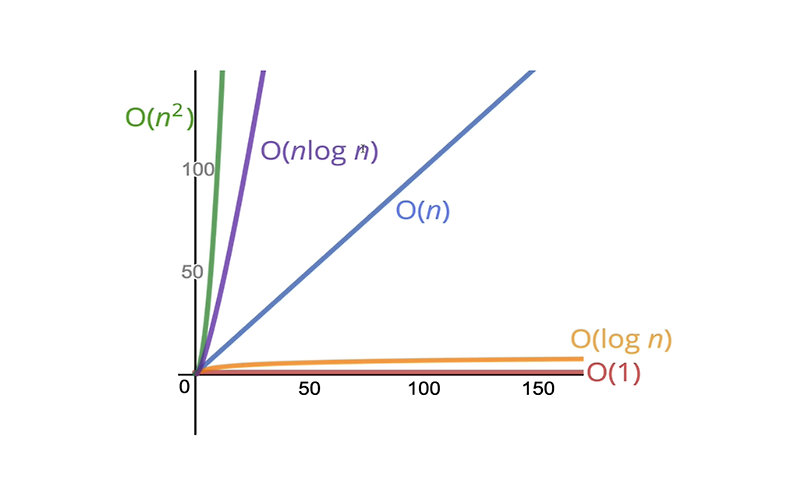
n의 값이 커져도 전반적으로 실행 시간에 큰 변화가 없는것을 O(1)이라고 한다.
n의 값이 커진만큼 실행 시간이 비례적으로 또는 제곱으로 커지는 것을 O(n)**,O(n의제곱)**이라고 한다.

공간 복잡도(보조 공간 복잡도)

입력되는 것을 제외하고 알고리즘 자체가 필요로 하는 공간을 말한다.
불리언, 숫자, undefined, null은 자바스크립트에서 모두 불변 공간이다.
문자열,reference타입 배열과 객체는 O(n)의 공간을 차지한다.

예시를 보자면

function sum(arr) {
  let total = 0;
  for (let i = 0; i < arr.length; i++) {
    total += arr[i];
  }
  return total;
}

이 코드의 공간의 복잡도를 보자면 일단 배열의 모든 숫자를 더하는 것이다. 맨 마지막에 리턴할 것은 숫자들의 합이다. tatal, i 전부 숫자이다. 새로운 변수를 만드는 것이 아닌 기존의 배열의 합을 만드는 것이다. o(n)

function double(arr) {
  let newArr = [];
  for (let i = 0; i < arr.length; i++) {
    newArr.push(2 * arr[i]);
  }
  return newArr;
}

새로운 배열을 만들어내기때문에 배열의 입력과 비례해서 길어진다. 차지하는 공간은 입력 된 배열 크기과 비례해서 커진다. O(n)

로그와 섹션

로그 개념을 완전히 습득할 필요는 없지만 이 개념을 짚어야 한다. O(1), O(n), O(n의제곱)처럼 간단하지 않을 수도 있기 때문이다.

로그는 뭘까? 지수 함수의 짝이다. 2의 3승이 8인것처럼, log 2 이진 함수가 가장 흔하다.

재귀라는 주제가 있다. 이 부분에서 로그를 다시 접할 것이다. 재귀는 시간 복잡도가 아닌 공간복잡도와 관련이 있다.