JS => 자료구조 (Tree)

Tree

자료구조 Tree는 이름 그대로 나무의 형태를 가지고 있다.
정확히는 나무를 거꾸로 뒤집어 놓은 듯한 모습을 가지고 있다.

그래프의 여러 구조 중 무방향 그래프의 한 구조로,
하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮아 있다고 해서 트리 구조라 부른다.

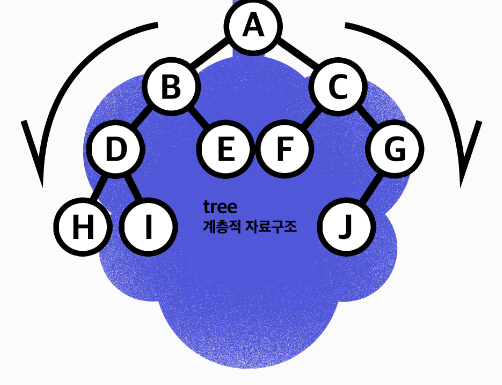
위 사진처럼,
트리 구조는 데이터가 바로 아래에 있는 하나 이상의 데이터에 무방향으로 연결된 계층적 자료구조다.

---

알아야 할 Tree 용어

1. 노드(Node): 트리 구조를 이루는 모든 개별 데이터
   
   
2. 루트(Root): 트리 구조의 시작점이 되는 노드
   
   
3. 부모 노드: 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
   
   
4. 자식 노드: 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
   
   
5. 리프: 트리 구조의 끝지점이고, 자식 노드가 없는 노드
   
   
6. 깊이: 위 그림에서 루트 A의 깊이는 0이고, B와 C의 깊이는 1이다. D, E, F, G의 깊이는 2이다.
   
   
7. 레벨: 위 그림에서 깊이가 0인 루트 A의 level은 1이고, 깊이가 1인 B와 C의 level은 2이다. D, E, F, G의 레벨은 3이다.
   
   
8. 높이: 위 그림에서 H, I, E, F, J의 높이는 0이고, D와 G의 높이는 1이다. B와 C의 높이는 2이다.

Tree 사용의 실사용 예제로,
월드컵 토너먼트 대진표, 가계도(족보), 조직도 등이 있다.

---

Binary Serch Tree

트리 구조는 편리한 구조를 전시하는 것 외에 효율적인 탐색을 위해 사용하기도 한다.

많은 트리의 모습 중,
가장 간단하고 많이 사용하는 이진 트리(binary tree)와 이진 탐색 트리(binary search tree)가 있다.

1. 이진트리(Binary tree)

자식 노드가 최대 두 개인 노드들로 구성된 트리이다.
두 개의 자식 노드는 왼쪽과 오른쪽 자식 노드로 나눌 수 있다.

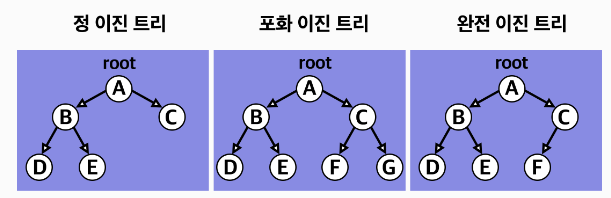
이진 트리는 자료의 삽입, 삭제 방법에 따라
정 이진 트리, 완전 이진 트리, 포화 이진 트리로 나뉜다.

2. 이진탐색트리(binary search tree)

이진 탐색 트리는 모든 왼쪽 자식의 값이 루트나 부모보다 작고,
모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징을 가진다.

이진 탐색 트리는 균형 잡힌 트리가 아닐 때,
입력되는 값의 순서에 따라 한쪽으로 노드들이 몰리게 될 수 있어,
트리의 구조를 재조정하는 과정을 거치는 알고리즘을 추가할 수 있다.

binary search tree 구현

class BinarySearchTree {
  constructor(value) {
		// constructor로 만든 객체는 이진 탐색 트리의 Node가 된다.
    this.value = value;
    this.left = null;
    this.right = null;
  }
<br>
  insert(value) { // 이진 탐색 트리의 삽입하는 메서드
    if (value < this.value) { // 입력값이 현재 노드의 값보다 작다면
      if (this.left === null) { // 왼쪽 노드가 비어있다면
        this.left = new BinarySearchTree(value); //  node 인스턴스 형성
      } else {
        this.left.insert(value) // 비어있지 않다면 값을 넣어준다.
      }
    } else if (value > this.value) { // 입력값이 현재 노드의 값보다 크다면
      if (this.right === null) { // 오른쪽 노드가 비어있다면
        this.right = new BinarySearchTree(value); // node 인스턴스 형성
      } else {
        this.right.insert(value) // 비어있지 않다면 값을 넣어준다.
      }
    } else { //그것도 아니라면, 입력값이 트리에 들어 있는 경우이기에 아무것도 하지 않는다.
      return;
    }
  }
<br>
contains(value) { // 이진 탐색 트리 안에 해당 값이 포함되어 있는지 확인하는 메서드
if (this.value === value) { // 입력값이 현재 노드의 값과 같다면
  return true;
}
if (value < this.value) { // 입력값이 현재 노드의 값 보다 작다면
  if(this.left === null) { // 왼쪽 노드가 없다면
    return false;
  }
  else if( this.left.value === value) { // 왼쪽 노드의 값과 입력값이 같다면
    return true;
  } 
    return this.left.contains(value) // 일치하지 않다면 왼쪽 노드로 이동하여 다시 탐색한다. 
}
if (value > this.value) {
   if(this.right === null) {
    return false;
  }
  if(this.right.value === value) {
    return true;
  }
    return this.right.contains(value)
} 
return false;
}
<br>
  // tree를 전위 순회
  preorder(callback) {
    callback(this.value);
    if (this.left) {
      this.left.preorder(callback);
    }
    if (this.right) {
      this.right.preorder(callback);
    }
  }
  // tree를 중위 순회
  inorder(callback) {
    if (this.left) {
      this.left.inorder(callback);
    }
    callback(this.value);
    if (this.right) {
      this.right.inorder(callback);
    }
  }
  //tree를 후위 순회
  postorder(callback) {
    if (this.left) {
      this.left.postorder(callback);
    }
    if (this.right) {
      this.right.postorder(callback);
    }
    callback(this.value);
  }
}