문제 설명

당신은 순서대로 n개의 퍼즐을 제한 시간 내에 풀어야 하는 퍼즐 게임을 하고 있습니다. 각 퍼즐은 난이도와 소요 시간이 정해져 있습니다. 당신의 숙련도에 따라 퍼즐을 풀 때 틀리는 횟수가 바뀌게 됩니다. 현재 퍼즐의 난이도를 diff, 현재 퍼즐의 소요 시간을 time_cur, 이전 퍼즐의 소요 시간을 time_prev, 당신의 숙련도를 level이라 하면, 게임은 다음과 같이 진행됩니다.

• diff ≤ level이면 퍼즐을 틀리지 않고 time_cur만큼의 시간을 사용하여 해결합니다.
• diff > level이면, 퍼즐을 총 diff - level번 틀립니다. 퍼즐을 틀릴 때마다, time_cur만큼의 시간을 사용하며, 추가로 time_prev만큼의 시간을 사용해 이전 퍼즐을 다시 풀고 와야 합니다. 이전 퍼즐을 다시 풀 때는 이전 퍼즐의 난이도에 상관없이 틀리지 않습니다. diff - level번 틀린 이후에 다시 퍼즐을 풀면 time_cur만큼의 시간을 사용하여 퍼즐을 해결합니다.
  
  
  예를 들어 diff = 3, time_cur = 2, time_prev = 4인 경우, level에 따라 퍼즐을 푸는데 걸리는 시간은 다음과 같습니다.
  
  
• level = 1이면, 퍼즐을 3 - 1 = 2번 틀립니다. 한 번 틀릴 때마다 2 + 4 = 6의 시간을 사용하고, 다시 퍼즐을 푸는 데 2의 시간을 사용하므로 총 6 × 2 + 2 = 14의 시간을 사용하게 됩니다.
• level = 2이면, 퍼즐을 3 - 2 = 1번 틀리므로, 6 + 2 = 8의 시간을 사용하게 됩니다.
• level ≥ 3이면 퍼즐을 틀리지 않으며, 2의 시간을 사용하게 됩니다.
  퍼즐 게임에는 전체 제한 시간 limit가 정해져 있습니다. 제한 시간 내에 퍼즐을 모두 해결하기 위한 숙련도의 최솟값을 구하려고 합니다. 난이도, 소요 시간은 모두 양의 정수며, 숙련도도 양의 정수여야 합니다.
  
  
  퍼즐의 난이도를 순서대로 담은 1차원 정수 배열 diffs, 퍼즐의 소요 시간을 순서대로 담은 1차원 정수 배열 times, 전체 제한 시간 limit이 매개변수로 주어집니다. 제한 시간 내에 퍼즐을 모두 해결하기 위한 숙련도의 최솟값을 정수로 return 하도록 solution 함수를 완성해 주세요.

제한 사항

• 1 ≤ diffs의 길이 = times의 길이 = n ≤ 300,000
  • diffs[i]는 i번째 퍼즐의 난이도, times[i]는 i번째 퍼즐의 소요시간입니다.
  • diffs[0] = 1
  • 1 ≤ diffs[i] ≤ 100,000
  • 1 ≤ times[i] ≤ 10,000
• 1 ≤ limit ≤ 1015
  • 제한 시간 내에 퍼즐을 모두 해결할 수 있는 경우만 입력으로 주어집니다.

입출력의 예

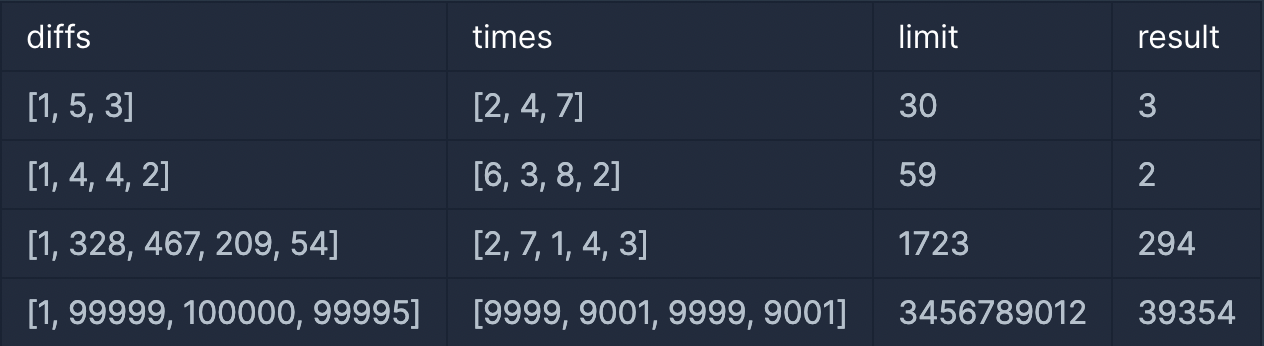
1. 풀이 방향성

먼저 생각난것은 반복문으로 1부터 시작해서 늘려가며 찾는 방법이었지만 문제가 틀리면 이전 문제부터 다시 계산해야 하는 문제의 특성과 입출력의 예의 엄청나게 높은 입력값을 보고 그냥 무작정 늘려가는게 아닌
이진 탐색(Binary search)으로 답을 구해야 한다는 것을 알았다.
간단한 예시로
숫자 1부터 100까지 중 62라는 목표값을 찾아야 한다면 1부터 100의 중앙값인 50을 놓고 62와 맞는지 확인.
목표값이 50보다 높다면 이제 51부터 100 숫자의 중앙값인 75를 놓고 목표값과 비교, 이런식으로 자르고 잘라 목표값을 찾는 방식이다.

• 범위는 diffs의 제일 낮은 값부터 제일 높은 값.
• 코드가 지저분해 질 것 같아 퍼즐을 풀 수 있는 level인지 확인하는 puzzle 함수를 따로 작성했다.

2. 풀이 결과

# 현재 레벨이 제한 시간내로 퍼즐을 풀 수 있는지 확인하는 puzzle 함수
def puzzle(diffs, times, limit, level):
    time = 0
    for i in range(len(diffs)):
        if diffs[i] <= level:
            time += times[i];
        
        if diffs[i] > level:
            time += ((times[i]+times[i-1])*(diffs[i]-level)+times[i]);
        
        if time > limit:
            return False;
    
    return True;
        

def solution(diffs, times, limit):
    lv_min = min(diffs);
    lv_max = max(diffs);
    lv_mid = 1;
    answer = 0;
    
    while lv_min <= lv_max:
        lv_mid = (lv_max + lv_min) // 2;
        
        # 퍼즐을 풀 수 있다면 더 아래의 레벨을 찾기 위해 max 값을 내림
        if puzzle(diffs, times, limit, lv_mid):
            lv_max = lv_mid - 1;
            answer = lv_max
        
        #퍼즐을 풀 수 없다면 퍼즐을 풀 수 있는 레벨을 찾기 위해 min 값을 올림
        if not puzzle(diffs, times, limit, lv_mid):
            lv_min = lv_mid + 1;
            answer = lv_min
            
    # 정답이 1인 경우 while문에서 최종적으로 1을 빼고 종료돼서 0이 되어버리기 때문에 if문으로 확인(14번 테스트 케이스)
    if answer == 0:
        answer += 1;
    
    # while 반복문을 빠져나올 때 1을 빼고 빠져나온 경우를 대비해 puzzle 함수로 최종 확인 
    if puzzle(diffs, times, limit, answer):
        return answer;

    else:
        return answer+1;

탐색 범위가 넓어 시간 초과가 뜰 것 같다면 이진 탐색을 사용하자!