
✅ TIL
이번 유닛에서는 조금 특별한 문제 해결 방법을 사용한다.
바로 자기 자신을 호출하는 함수인 재귀(recursion) 함수 를 활용하는 방법이다.
재귀함수
재귀란 무엇일까? 표준국어대사전에서는 다음과 같이 정의하고 있다.
재귀(再歸) : 원래의 자리로 되돌아가거나 되돌아옴.
재귀의 시각적 예시를 든다면 계속해서 원래의 상태로 돌아오는 아래 이미지와 같을 것이다.

위 정의와 예시를 참고하여 재귀를 코드로 표현하면 다음과 같이 작성할 수 있을 것이다.
function recursion () {
console.log("This is")
console.log("recursion!")
recursion()
}
recursion 함수를 호출했더니, 자기 자신을 끝없이 호출하면서 같은 코드가 계속해서 실행되는 것을 볼 수 있다.
이 recursion 함수처럼 자기 자신을 호출하는 함수를 재귀 함수라고 한다.
재귀 함수를 잘 활용하면 반복적인 작업을 해야 하는 문제를 좀 더 간결한 코드로 풀어낼 수 있다.
재귀로 문제 해결하기
💡 문제: 자연수로 이루어진 리스트(배열)를 입력받고, 리스트의 합을 리턴하는 함수 arrSum을 작성하세요.
물론 재귀 없이 반복문으로 해결하는 방법도 있다.
하지만 이번 챕터는 재귀를 배우는 것이 목적이니, 차근차근 따라오며 재귀를 이해해 보자.
-
문제를 좀 더 작게 쪼갠다.
-
1번과 같은 방식으로, 문제가 더는 작아지지 않을 때까지, 가장 작은 단위로 문제를 쪼갠다.
-
가장 작은 단위의 문제를 풂으로써 전체 문제를 해결한다.
이 단계를 적용해서 arrSum 함수를 작성해 보고, 배열 [1, 2, 3, 4, 5]의 합을 구하는 과정을 재귀로 풀어보자.
1. 문제를 작게 쪼개기
어떻게 하면 arrSum 함수로 [1, 2, 3, 4, 5]의 합을 구하는 과정을 더 작게 쪼갤 수 있을까?
단순하게 생각해 보면, 배열의 합을 구할 때 [1, 2, 3, 4, 5]의 합을 구하는 것보다 [2, 3, 4, 5]의 합을 구하는 것이
더 작은 문제이고, 여기서 또 [2, 3, 4, 5]의 합을 구하는 것보다 [3, 4, 5]의 합을 구하는 것이 더 작은 문제일 것이다.
위 방식으로 문제를 쪼갠 것을 코드로 표현하면 다음과 같다.
arrSum([1, 2, 3, 4, 5]) === 1 + arrSum([2, 3, 4, 5])
arrSum([2, 3, 4, 5]) === 2 + arrSum([3, 4, 5])
...2. 문제를 가장 작은 단위로 쪼개기
위에서 문제를 쪼갠 방식을 반복해서 문제를 계속해서 쪼개면 더 이상 쪼갤 수 없는 상태에 도달하게 된다.
...
arrSum([3, 4, 5]) === 3 + arrSum([4, 5])
arrSum([4, 5]) === 4 + arrSum([5])
arrSum([5]) === 5 + arrSum([])마지막에는 arrSum이 빈 배열을 받게 되면서 문제를 더 이상 쪼갤 수 없게 되었다.
이로써 문제를 가장 작은 단위까지 쪼갰다고 할 수 있다.
3. 문제 해결하기
문제가 더 쪼개지지 않게 되면, 가장 작은 단위의 문제를 해결한다.
문제를 쪼갤 때 같은 방식으로 쪼갰기 때문에, 가장 작은 단위의 문제를 해결한 방식으로 문제 전체를 해결할 수 있게 된다.
2번에서 도달한 가장 작은 문제는 arrSum([])이었다. 빈 배열의 합은 0이므로, 0을 리턴해주면 끝이다.
이렇게 가장 작은 문제를 해결하는 순간, 아래 코드처럼 쪼개졌던 문제가 거꾸로 거슬러 올라가면서 합쳐지게 된다.
arrSum([]) === 0; // <-- 문제가 더는 작아지지 않는 순간
// 가장 작은 경우의 해결책을 적용합니다.
arrSum([5]) === 5 + arrSum([]) === 5 + 0 === 5;
arrSum([4, 5]) === 4 + arrSum([5]) === 4 + 5 === 9;
arrSum([3, 4, 5]) === 3 + arrSum([4, 5]) === 3 + 9 === 12;
arrSum([2, 3, 4, 5]) === 2 + arrSum([3, 4, 5]) === 2 + 12 === 14;
arrSum([1, 2, 3, 4, 5]) === 1 + arrSum([2, 3, 4, 5]) === 1 + 14 === 15;
위 단계를 반영해서 arrSum 함수를 완성해 보면 다음과 같다.
function arrSum (arr) {
// 빈 배열을 받았을 때 0을 리턴하는 조건문
// --> 가장 작은 문제를 해결하는 코드 & 재귀를 멈추는 코드
if (arr.length === 0) {
return 0
}
// 배열의 첫 요소 + 나머지 요소가 담긴 배열을 받는 arrSum 함수
// --> 재귀(자기 자신을 호출)를 통해 문제를 작게 쪼개나가는 코드
return arr.shift() + arrSum(arr)
}
arrSum 함수가 내부에서 arrSum 함수를 호출하면서 문제가 쪼개어져 나가고,
결국 문제를 더 이상 쪼갤 수 없는 arrSum([]) 까지 함수가 호출되는 것을 볼 수 있다.
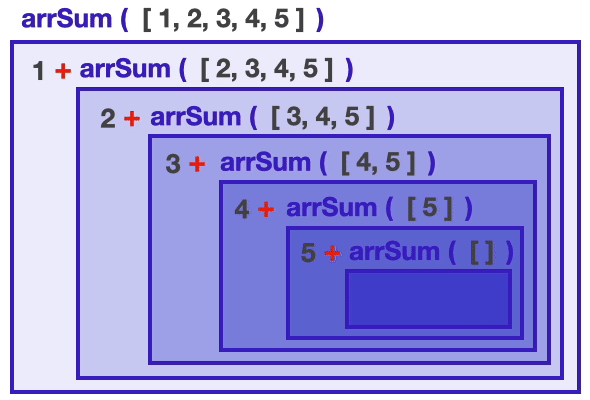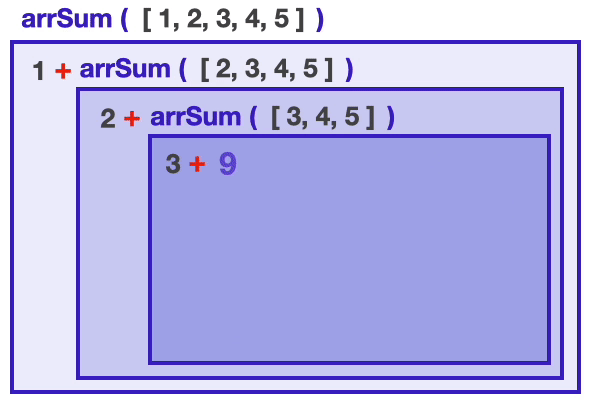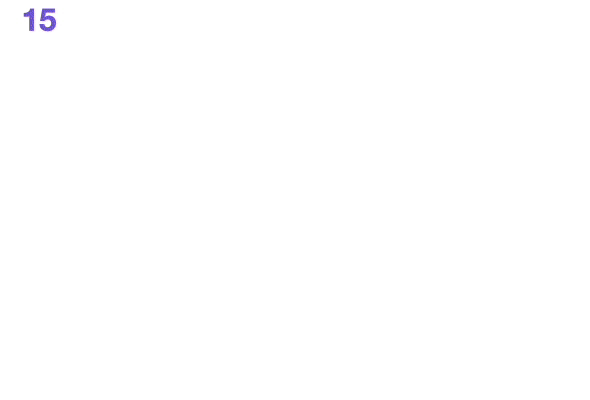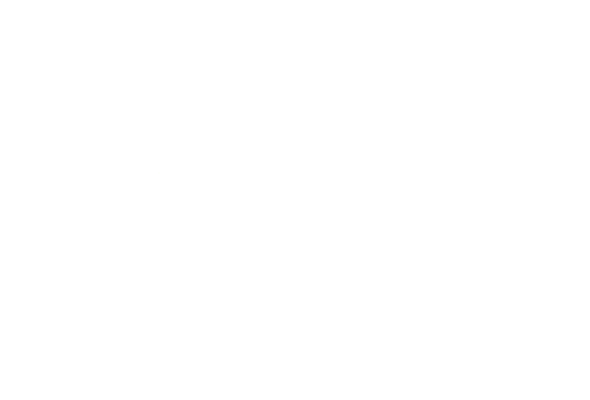
arrSum([])는 조건문에 의해 더 이상 자기 자신을 호출하지 않고, 숫자 0을 리턴하면서 종료된다.
그 결과 중첩되어 있던 함수들도 연쇄적으로 숫자를 리턴하고,
최종적으로는 배열의 모든 요소의 합을 리턴하면서 문제가 해결된다.
재귀는 언제 사용하는 게 좋을까?
재귀는 다음과 같은 상황에서 매우 적합하다.
- 주어진 문제를 비슷한 구조의 더 작은 문제로 나눌 수 있는 경우
- 중첩된 반복문이 많거나 반복문의 중첩 횟수(number of loops)를 예측하기 어려운 경우
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
for (let k = 0; k < n; k++) {
for (let l = 0; l < n; l++) {
for (let m = 0; m < n; m++) {
for (let n = 0; n < n; n++) {
for (let o = 0; o < n; o++) {
for (let p = 0; p < n; p++) {
// do something
someFunc(i, j, k, l, m, n, o, p);
}
}
}
}
}
}
}
}모든 재귀 함수는 반복문(while문 또는 for문)으로 표현할 수 있다.
그러나 재귀를 적용할 수 있는 대부분의 경우에는, 재귀를 적용한 코드가 더욱 간결하고 이해하기 쉽다.
이 밖에도, 재귀는 알고리즘 문제의 많은 부분을 차지한다.
앞으로 만나게 될 다양한 과제와 기업의 입사 시험(코딩 테스트, 알고리즘 테스트 등)이나 직무면접에서 활용할 수 있다.
재귀의 활용
1. 재귀 함수의 입력값과 출력값 정의하기
재귀적으로 사고하는 데에 가장 먼저 해야 할 일은 문제를 가장 추상적으로 또는, 가장 단순하게 정의하는 것이다.
함수의 입출력 값을 정의하는 것은 그 첫 출발점이며,
재귀 함수를 통해 풀고자 하는 문제, 즉 도달하고자 하는 목표를 정의하는 데 도움이 된다.
함수 arrSum의 경우 number 타입을 요소로 갖는 배열을 입력으로 받고, number 타입을 리턴한다.
이를 좀 더 간단하게 표기하면 다음과 같다.
- arrSum: [number] => number ← 입출력 값 정의
2. 문제를 쪼개고 경우의 수를 나누기
다음으로는 주어진 문제를 어떻게 쪼갤 것인지 고민한다.
문제를 쪼갤 기준을 정하고, 정한 기준에 따라 문제를 더 큰 경우와 작은 경우로 구분할 수 있는지 확인한다.
일반적으로, 입력값을 이 기준으로 정한다. 이때 중요한 관점은 입력값이나 문제의 순서와 크기이다.
주어진 입력값 또는 문제 상황을 크기로 구분할 수 있거나, 순서를 명확하게 정할 수 있다면 문제를 구분하는 데 도움이 된다.
그리고 구분된 문제를 푸는 방식이 순서나 크기와 관계없이 모두 같다면, 문제를 제대로 구분한 것이다.
- 함수 arrSum의 경우 입력값인 배열의 크기에 따라, 더 작은 문제로 나눌 수 있다. 그리고 arrSum([1, 2, 3, 4])를 구하는 방법과 arrSum([2, 3, 4])을 구하는 방법은 동일하므로, 이 구분은 적절하다고 판단할 수 있다.
이제 문제에서 주어진 입력값에 따라, 경우의 수를 나눈다.
일반적으로 문제를 더 이상 쪼갤 수 없는 경우와 그렇지 않은 경우로 나눈다.
- 함수 arrSum은 입력값이 빈 배열인 경우와 그렇지 않은 경우로 나눌 수 있다. 각각 다른 방식으로 처리해야 한다.
- arrSum: [number] => number
- arrSum([ ]) ← 입력값이 빈 배열인 경우
- arrSum([요소1, 요소2, ... , 요소n]) ← 그렇지 않은 경우
3. 단순한 문제 해결하기
문제를 여러 경우로 구분한 다음, 가장 해결하기 쉬운 문제부터 해결한다. 이를 재귀의 기초(base case)라고 부른다.
재귀의 기초는 나중에 재귀 함수를 구현할 때, 재귀의 탈출 조건(재귀 호출이 멈추는 조건)을 구성한다.
탈출 조건이 없는 경우 재귀 함수는 끝없이 자기 자신을 호출하게 된다. 그렇다고 문제를 덜 쪼갠 상태에서 탈출 조건을 세우는 경우 문제를 제대로 해결할 수 없게 된다. 그만큼 문제를 최대한 작게 쪼갠 후에 문제를 해결하는 것이 중요하다.
- 함수 arrSum을 더 이상 쪼갤 수 없는 경우는 입력값이 빈 배열일 경우이고, 이때 arrSum([])의 리턴값은 0이다.
- arrSum: [number] => number
- arrSum([ ]) === 0 ← 입력값이 빈 배열인 경우 : 해결!
- arrSum([요소1, 요소2, ... , 요소n])
4. 복잡한 문제 해결하기
남아있는 복잡한 경우를 해결한다.
- 길이가 1 이상인 배열이 함수 arrSum에 입력된 경우, 입력된 배열을 배열의 첫 요소와 나머지 요소를 입력값으로 갖는 문제로 쪼개고, 둘을 더한다.
- arrSum: [number] => number
- arrSum([ ]) === 0
- arrSum([요소1, 요소2, ... , 요소n]) === 요소1 + arrSum([요소2, ..., 요소n]) ← 그렇지 않은 경우 : 해결!
- 배열을 첫 요소와 더 작은 문제로 쪼개는 방법만 안다면, 함수 arrSum을 재귀적으로 구현할 수 있다.
5. 코드 구현하기
function arrSum(arr) {
// base case : 문제를 더 이상 쪼갤 수 없는 경우 (재귀의 기초)
if (arr의 길이가 0인 경우) {
return 0;
}
// recursive case : 그렇지 않은 경우
return 요소1 + arrSum([요소2, ... , 요소n]);
}💬 Sprint Review
// ✅ 구현한 코드
function unpackGiftbox(giftBox, wish) {
if (!giftBox?.length || !wish?.length) {
return false;
}
return giftBox.some((item) => {
if (typeof item === 'string') {
return item === wish;
} else if (Array.isArray(item)) {
return unpackGiftbox(item, wish);
}
});
}💬 Review
.some이라는 메서드를 처음 알게 되었다.
배열 안의 어떤 요소라도 주어진 판별 함수를 적어도 하나라도 통과하는지 테스트한다고 한다.
- 배열에서 주어진 함수가 true를 반환하면 true를 반환
- 배열에서 주어진 함수가 false를 반환하면 false를 반환
- 이 메서드는 배열을 변경하지 않는다.
먼저, giftBox와 wish 각각 배열과 문자열이 빈 경우에 false를 반환하도록 조건을 세워줬다.
그 후 바로 본문을 giftBox.some() 메서드에 전달되는 콜백 함수를 정의했다.
.some 메서드와 화살표 함수를 사용하여 최종적으로 boolean 값이 반환해도록 했다.
요소들이 만약 문자열이라면, giftBox 배열의 각 요소를 순회하면서 문자열인 경우 wish와 일치하는지 확인하고,
배열인 경우 재귀적으로 unpackGiftbox 함수를 호출한다.

// ✅ 구현한 코드
function flattenArr(arr) {
return arr.reduce(function (result, item) {
if (Array.isArray(item)) {
const flattened = flattenArr(item);
return [...result, ...flattened];
} else {
return [...result, item];
}
}, []);
}💬 Review
주어진 배열 arr을 reduce 메서드를 사용하여 순회하면서 각 요소를 확인한다.
만약 현재 요소가 배열인 경우, flattenArr 함수를 재귀적으로 호출하여 해당 배열을 평면화한다.
재귀 호출 결과를 flattened 변수에 할당한다.
그리고 result 배열과 flattened 배열을 전개 연산자(...)를 사용하여 합친다.
이렇게 함으로써 현재 요소를 평면화한 결과를 result 배열에 추가한다.
만약 현재 요소가 배열이 아닌 경우, 즉 숫자, 문자열 등의 원시 값인 경우에는 그대로 result 배열에 추가한다.
순회가 완료되면 최종적으로 평면화된 배열이 완성된다.
초기값으로 빈 배열([])을 사용하여 reduce 메서드를 호출하고 있으므로,
reduce 메서드의 마지막 반환값이 최종 결과인 평면화된 배열이다.
💡 Error Note.
💡 .some과 .reduce 메서드
- 처음에는 첫 번째 문제를 .reduce 메서드로 풀고 있었으나, 결과 값이 boolean 이므로 .some을 채택
- .reduce() 메서드는 배열의 각 요소를 순회하면서 주어진 콜백 함수를 실행하여 하나의 값을 계산하는데 사용
- .some() 메서드는 배열의 각 요소를 순회하면서 주어진 조건을 만족하는 요소가 존재하는지 여부를 확인하는데 사용
💡 옵셔널 체이닝(Optional Chaining) 연산자
- Zoom 시간에 멘토님이 !giftBox.length가 아닌
!giftBox?.length를 사용하는 것을 목격 - 처음에
?가 오타인 줄 알았으나, 이는 옵셔널 체이닝이라는 연산자였다. - 이 연산자는 객체 체인 내에서 프로퍼티 또는 메서드에 접근할 때, 중간 단계의 값이 null 또는 undefined인 경우 에러를 발생시키지 않고 undefined를 반환하는 기능을 제공한다.
- ✅ 모든 상황에서 옵셔널 체이닝을 사용하는 것이 항상 쓰는 것이 좋은 것은 아니다.
- ex) 중간 단계의 값이 null 또는 undefined인 경우 에러나 다른 처리 로직이 필요한 경우.
