알고리즘의 정의

: 문제를 해결할 수 있는 잘 정의된(well defined) 유한(finite)시간 내에 종료되는 계산적인(computational) 절차(precedure)

Algorithm과 Method의 차이점
알고리즘은 유한 시간내에 종료되나, method는 유한 시간내에 종료 되는지 모른다!

알고리즘 분석 방법

문제의 표기 방법

• 문제 : 답을 찾고자 던지는 질문
• 파라미터(parameter) : 문제에서 특정값이 주어지지 않은 변수
• 입력 : parameter에 특정 값을 지정한 것
• 출력 : 주어진 입력에 대한 문제의 답

Ex 1.1) Sorting

• 문제 : n개의 수로 구성된 리스트 S 를 비내림차순(nondecreasing order)으로 정렬(sort)하라
• 파라미터: S, n
• 사례(instance) – 파라미터에 어떤 값을 대입한 경우

Ex 1.2) Searching

• 문제: 어떤 수 x가 n개의 수로 구성된 리스트 S 에 있는지 결정하라. S 에 있으면 “예”, 없으면 “아니오”로 답하시오
• 파라미터: S, n, x

Pseudo-code(의사코드)

: 직접 실행할 수 있는 프로그래밍언어는 아니지만, 거의 실제 프로그램에 가깝게 계산과정을 표현할 수 있는 언어이다. 간결하면서 정확하게 의미를 표현가능하다. 알고리즘은 의사코드를 사용하여 표현한다.

배열 (Array)
: 공통의 성질을 갖는 변수가 여러 개 일 때 하나의 변수명을 정하고, 위치를
나타내는 인덱스를 이용해서 변수를 나타내는 자료구조 (data structure)

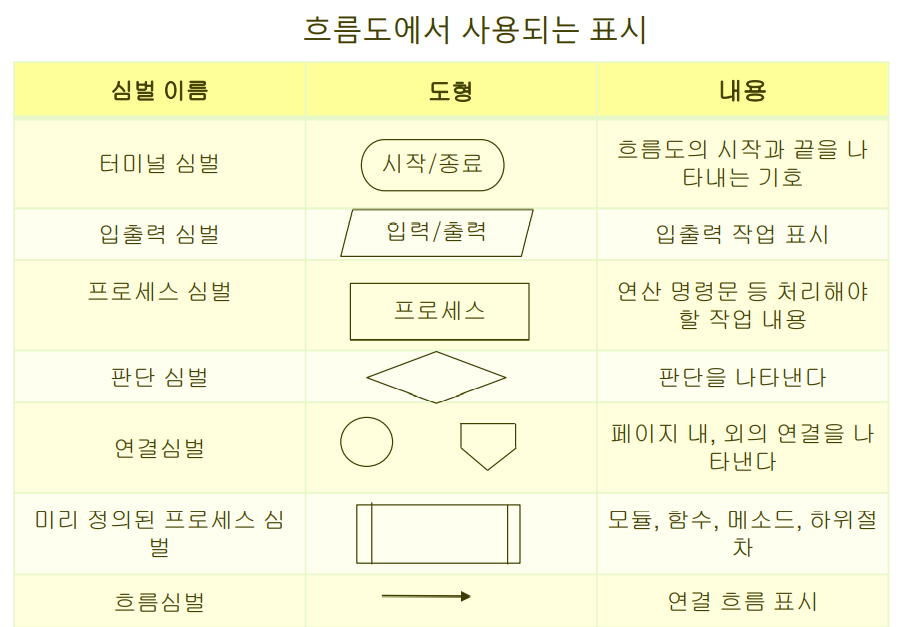
[배열에 저장된 10개의 수 중 최대값 찾기]

• Pseudo-code
  1) a[0]의 데이터를 임시로 최대값 M으로 설정
  2) a[1]의 값과 M과 비교해서, a[1]이 더 크면 a[1]을 M으로 재설정, 아니면 a[2]값 비교로 이동
  3) step 2를 나머지 데이터에 대해서 수행
  4) M이 데이터의 최대값
  

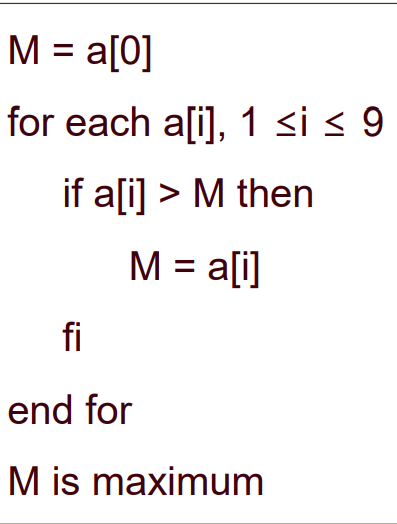
Flow-chart(흐름도)

Examples

Alg 1.1 순차검색 알고리즘

Pseudo-code

구현

1) Python

# Seqeuntial Search

def seqsearch(s, x):
    loc = -1
    for i in range(len(s)):
        if s[i] == x:
            loc = i
    return loc

s = [3,5,2,1,7,9]
loc = seqsearch(s,4)
print(loc)

Alg 1.2 배열의 수 더하기

Pseudo-code

구현

1) Python

# Sum of elements of array

def sum1(s):
    result = 0
    for a in s:
        result += a
    return result

def sum2(s):
    result = 0
    for i in range(len(s)):
        result += s[i]
    return result

s = [3,5,2,1,7,9]
answer1 = sum1(s)
answer2 = sum2(s)

print(answer1, answer2)

Alg 1.3 교환정렬

Pseudo-code

구현

1) Python

# Select1ion Sort - nondecreasing order
def Selection_Sort(S):
    for i in range(len(S)):
        for j in range(i+1, len(S)):
            if S[j] < S[i]:
                temp = S[i]
                S[i] = S[j]
                S[j] = temp
    return S

s=[3,2,5,7,1,9,4,6,8]
s = Selection_Sort(s)
print(s)

Alg 1.4 행렬의 곱셈

Pseudo-code

구현

# Matrix Multiplication

def Matrix_Multiplication(a, b):
    result = [[0] * len(b) for row in range(len(a))]
    for i in range(len(a)):
        for j in range(len(b)):
            for k in range(len(a[0])):
                result[i][j] += a[i][k] * b[k][j]
    return result

a = [[1,2], [3,4]]
b = [[4,1], [1,0]]
print(Matrix_Multiplication(a,b))

Alg 1.5 Binary Search

Pseudo-code

구현

# Binary Search
def binary_search(data, item, low, high):
    location = -1
    while (low <= high) and (location==-1):
        mid = int((low + high) / 2)
        if data[mid] == item:
            location = mid
        elif data[mid] > item:
            high = mid-1
        else:
            low = mid+1
    return location

data = [1,3,5,6,7,9,10,14,17,19]
n = len(data)
location = binary_search(data, 9, 0, n-1)
print(location)

Alg 1.6 Fibonacci

Pseudo-code
1) Recursion(재귀)

2) Iteration(반복)

구현

# Fibonacci

# Recursive way
def fib1(n):
    if n <= 1:
        return n
    else:
        return fib1(n-1) + fib1(n-2)

# Iterative way
def fib2(n):
    fib = [0 for i in range(n+1)]
    if n > 0:
        fib[1] = 1
        for i in range(2,n+1):
            fib[i] = fib[i-1] + fib[i-2]
    return fib[n]

알고리즘의 분석

분석 방법의 종류

Every-case analysis

: Input data의 size에만 종속된다. Input data의 value와는 무관하다.

• Worst-case analysis
• Average-case analysis
• Best-case analysis