Calculate destination with start point, distance, bearing in Kotlin
이 글은 기존 운영했던 WordPress 블로그인 PyxisPub: Development Life (pyxispub.uzuki.live) 에서 가져온 글 입니다. 모든 글을 가져오지는 않으며, 작성 시점과 현재 시점에는 차이가 많이 존재합니다.
작성 시점: 2018-06-19
도입
몇 달 전에, 좌표에 관련된 어떤 기능을 개발할 일이 있었다. 바로, '내 위치 주변 1km 에 있는 매장을 전부 가져오기' 였는데, 이를 좀 더 상세하게 표현하면 주변이라 함은 360' 를 의미하니 아래처럼 표현할 수 있다.
시작 지점으로부터 x km 떨어지고 y 방향 기울어진 목적 지점을 구하고, 이 범위 안에 포함되는 매장을 전부 조회하기
이를 위해서는 북동쪽, 남서쪽에 대한 좌표를 가져와 해당 범위 안에 있는 좌표를 조회하면 된다. 이 글에서는 먼저 현재 위치에 대해 36방향 + 1km 떨어진 곳의 좌표를 구하고, 원래 목표였던 북동쪽과 남서쪽에 대한 좌표를 구하려 한다.
이론
하버사인 공식(Haversine Formula) 은 주어진 지점에 대해 구 (Sphere) 의 두 지점 사이의 최단거리(great-circle distance) 를 구하는 공식이다. 풀어서 설명하자면, 우리가 사는 지구는 평면이 아닌 구 로 되어있다. 각 지점을 직선으로 긋는다고 해서 그 거리가 최단거리 라는 보장은 할 수 없는데, 이를 정리한 것이 하버사인 공식이다.
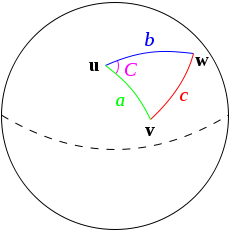
하버사인의 규칙, Wikipedia. https://en.wikipedia.org/wiki/Haversine_formula#/media/File:Law-of-haversines.svg
이를 사용하여 두 지점 간의 거리를 구하거나, 이 글의 목적인 한 지점에서 특정 거리에 대한 지점(= 목적 지점)을 구할 수도 있다.
목적 지점을 구하는 기본 공식은 다음과 같다.
φ2 = asin( sin φ1 ⋅ cos δ + cos φ1 ⋅ sin δ ⋅ cos θ ) λ2 = λ1 + atan2( sin θ ⋅ sin δ ⋅ cos φ1, cos δ − sin φ1 ⋅ sin φ2 )
여기서 각 문자열에 대한 정보는 다음과 같다.
- φ -> 주어진 위도
- λ -> 주어진 경도
- θ -> 북쪽으로부터 시계방향인 베어링
- δ -> d/R; d 는 주어진 거리, R은 라디안.
라디안이란 구 표면에 있어서의 호의 길이를 의미하는데, 여기에서는 6371.01 이라는 고정 값을 사용한다. 또한, 주어진 위, 경도 및 베어링은 각도(degree) 기반이기 때문에, 이를 라디안(Radian) 으로 바꿔서 계산을 수행하고 마지막에 각도로 다시 변경해야 하는데, 이에 대한 공식은 다음과 같다.
Degree -> Radian = Degree * Math.PI / 180 Radian -> Degree = Radian * 180 / Math.PI
λ2 까지 계산할 경우 -360 ~ 360 범위에 대한 경도값이 나오나, 경도는 -180 ~ 180 이 최대이므로 이를 normalize 하는 작업을 거친다. 다음은 이에 대한 공식이다.
λ3 = (λ2 + 540) % 360 - 180
이 5개의 공식을 풀어내면 목표인 목적 지점을 구할 수 있게 된다.
코틀린으로 구현하기
먼저 받아온 위도, 경도, 각도에 대해 Degree 를 Radian 으로 변경한다. 여기서는 Double 의 확장 함수로 toRadian, toDegree 을 만든다.
private fun Double.toRadian() = this * Math.PI / 180.0
private fun Double.toDegree() = this * 180.0 / Math.PI또한, 공식에서는 sin, cos를 사용하는데 이를 Math.sin(), Math.cos() 를 사용하여 만들기에는 다소 어려워 보일 수 있으니, 아래 확장 함수도 만들어둔다.
private fun Double.sin() = Math.sin(this)
private fun Double.cos() = Math.cos(this)위 함수를 사용해서 세 개의 정보를 모두 변환하여 각각 φ1, λ1, θ 로 만든다.
val radLatitude = startLatitude.toRadian()
val radLongitude = startLongitude.toRadian()
val radAngle = bearing.toRadian()그 다음, δ 를 구한다.
val distRadius = distance / 6371.01위 4개 지역 변수를 사용하여 위의 공식을 풀어내면 된다.
φ2 계산
공식을 살펴보자. φ2 = asin( sin φ1 ⋅ cos δ + cos φ1 ⋅ sin δ ⋅ cos θ ) 이를 프로그래밍 적으로 표현하면 다음과 같다. φ2 = Math.asin(φ1.sin() * δ.cos() + φ1.cos() * δ.sin() * θ.cos()) 실제 변수의 이름에 대입하면 다음과 같다.
latitude = Math.asin(radLatitude.sin() * distRadius.cos() + radLatitude.cos() * distRadius.sin() * radAngle.cos())이로서 목표지점에 대한 latitude 의 값이 나온다.
λ2 구하기
공식을 살펴보자. λ2 = λ1 + atan2( sin θ ⋅ sin δ ⋅ cos φ1, cos δ − sin φ1 ⋅ sin φ2 ) 마찬가지로 이를 프로그래밍 적으로 표현하면 다음과 같다. λ2 = λ1 + Math.atan2(θ.sin() * δ.sin() * φ1.cos(), δ.cos() − φ1.sin() * φ2.sin() ) 실제 변수의 이름에 대입하면 다음과 같다.
var longitude = radLongitude + Math.atan2(radAngle.sin() * distRadius.sin() * radLatitude.cos(), distRadius.cos() - radLatitude.sin() * latitude.sin())
마지막 공식을 사용해 나온 값을 normalize 하면 다음과 같다.
longitude = (longitude + 540) % 360 - 180
결과 반환
마지막으로 지금까지 Radian 값을 기반으로 계산을 수행했으니, 이를 다시 Degree 로 바꿔주면 된다.
latitude.toDegree() to longitude.toDegree()위 연산을 모두 담은 메서드는 다음과 같다.
/**
* Calculate destination with start point, distance, bearing
*
* given formula with Kotlin implementation
* φ2 = asin( sin φ1 ⋅ cos δ + cos φ1 ⋅ sin δ ⋅ cos θ )
* λ2 = λ1 + atan2( sin θ ⋅ sin δ ⋅ cos φ1, cos δ − sin φ1 ⋅ sin φ2 )
*
* φ is lat, λ is lng, θ is the bearing (clockwise from N),
* δ is the angular dist d/R; d being the dist travelled, R the earth’s radius
*
* @param startLati latitude of start point
* @param startLongi longitude of start point
* @param distance distance to calculate, unit is km (ex, 1.0 will 1km)
* @param bearing bearing to calculate, range is 0 to 360.
*/
@JvmStatic
fun calculateByAngle(startLati: Double, startLongi: Double, distance: Double, bearing: Double): Pair<Double, Double> {
val radLatitude = startLati.toRadian()
val radLongitude = startLongi.toRadian()
val radAngle = bearing.toRadian()
val distRadius = distance / 6371.01
val latitude = Math.asin(radLatitude.sin() * distRadius.cos() +
radLatitude.cos() * distRadius.sin() * radAngle.cos())
var longitude = radLongitude + Math.atan2(radAngle.sin() * distRadius.sin() * radLatitude.cos(),
distRadius.cos() - radLatitude.sin() * latitude.sin())
// normalize
longitude = (longitude + 540) % 360 - 180
return latitude.toDegree() to longitude.toDegree()
}테스트 코드
fun main(args: Array<String>) {
val target = "37.504416, 127.024419"
val originLatitude = target.replace(" ", "").split(",")[0].toDouble()
val originLongitude = target.replace(" ", "").split(",")[1].toDouble()
val distance = 1.0
println("=== [TEST START] ===")
println("origin: $originLatitude, $originLongitude")
println("distance: ${distance}km")
println()
println("testWithAngle :: i in 0 until 360 step 10")
(0 until 360 step 10)
.map { BoundCalculator.calculateByAngle(originLatitude, originLongitude, distance, it.toDouble()) }
.forEach { println("${it.first},${it.second}") }
println()
}
결과는 다음과 같이 나온다.
\=== [TEST START] ===
origin: 37.504416, 127.024419
distance: 1.0km
testWithAngle :: i in 0 until 360 step 10
37.513409201943354,127.02441900000065
37.51327255866217,127.02638777068461
37.512866782130125,127.02829670018794
37.51220420590747,127.03008776811927
37.51130496854182,127.03170654002517
37.51019640088359,127.0331038230291
37.50891219468923,127.0342371613944
37.50749137788997,127.03507212653854
37.50597712778582,127.03558336224015
37.50441545834116,127.03575535338179
37.50285382156253,127.03558289518287
37.50133966551645,127.03507124876813
37.499918992822515,127.03423597877277
37.498634963399496,127.03310247820143
37.49752658385741,127.0317051951975
37.496627523263115,127.03008658549764
37.495965091145784,127.02829582241753
37.49555940867182,127.02638730363384
37.49542279805665,127.02441900000065
37.49555940867182,127.02245069636744
37.495965091145784,127.02054217758375
37.496627523263115,127.01875141450364
37.49752658385741,127.01713280480378
37.498634963399496,127.01573552179985
37.499918992822515,127.01460202122851
37.50133966551645,127.01376675123315
37.50285382156253,127.01325510481843
37.50441545834116,127.0130826466195
37.50597712778582,127.01325463776114
37.50749137788997,127.01376587345624
37.50891219468923,127.01460083860688
37.51019640088359,127.01573417697219
37.51130496854182,127.01713145997611
37.51220420590747,127.01875023188201
37.512866782130125,127.02054129981335
37.51327255866217,127.02245022931668이를 https://www.mapcustomizer.com/ 사이트에 넣고 돌리면 다음과 같이 나온다.
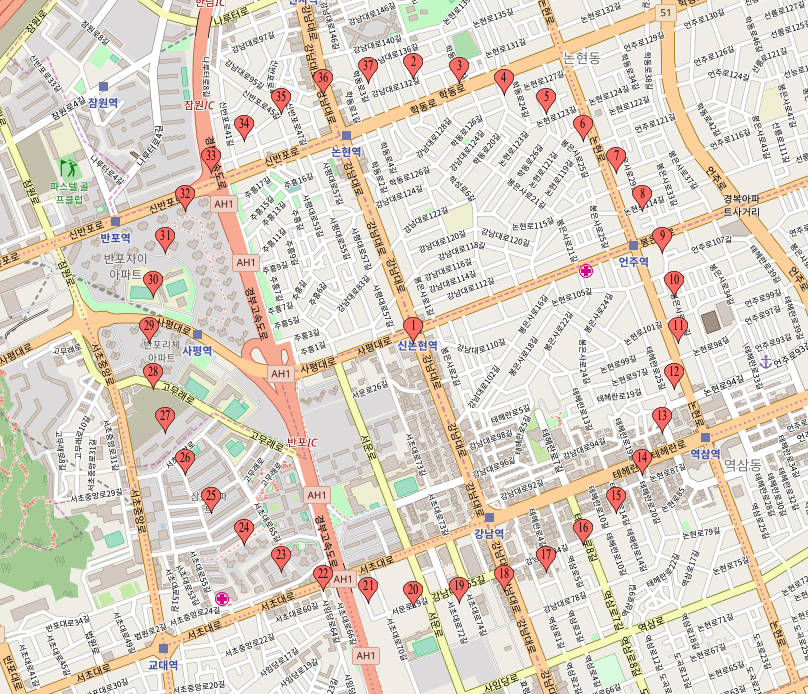
북동쪽, 남서쪽 구하기
시계 방향으로 생각해보았을 때, 8방향에 대한 각도는 다음과 같다.
- 북쪽 -> 0
- 북서쪽 -> 315
- 서쪽 -> 270
- 남서쪽 -> 225
- 남쪽 -> 180
- 남동쪽 -> 135
- 동쪽 -> 90
- 북동쪽 -> 45
여기에 정확도를 높이기 위해 지구의 기울기 (23.44) 를 빼면 어느정도 맞게 떨어진다.
먼저, 8방향에 대한 enum 을 정의한다.
enum class Direction(val angle: Double) {
North(0.0), West(270.0), South(180.0), East(90.0),
Northwest(315.0), Southwest(225.0), Southeast(135.0), Northeast(45.0)
}그리고 이 enum 을 파라미터로 받는 메서드를 만들어, 위에서 만든 메서드를 호출하게 한다.
/**
* Calculate destination with start point, distance, Direction
*
* Right-Angle-based angles are already declared in the Direction class.
* To further increase accuracy, it will reduce 'Axial tilt on Earth' (23.44 degree)
*
* @param startLatitude latitude of start point
* @param startLongitude longitude of start point
* @param distance distance to calculate, unit is km (ex, 1.0 will 1Km)
* @param direction Enumeration class for Direction with Right-Angle-based angles.
*/
@JvmStatic
fun calculateByDirection(startLatitude: Double, startLongitude: Double, distance: Double, direction: Direction) =
calculateByAngle(startLatitude, startLongitude, distance, direction.angle - 23.44)결과는 다음과 같이 나온다.
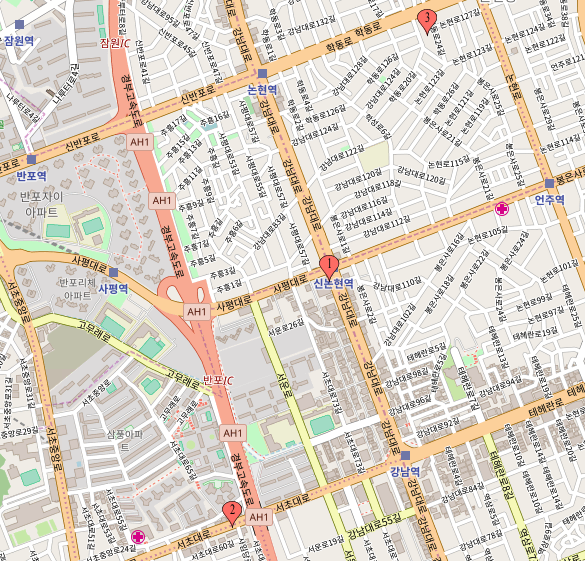
전체 코드
/**
* DestinationCalculator
*
* Calculate destination with start point, distance, Direction
*
* Created by Pyxis in 2018. 06. 19.
*/
object DestinationCalculator {
enum class Direction(val angle: Double) {
North(0.0), West(270.0), South(180.0), East(90.0),
Northwest(315.0), Southwest(225.0), Southeast(135.0), Northeast(45.0)
}
/**
* Calculate destination with start point, distance, Direction
*
* Right-Angle-based angles are already declared in the Direction class.
* To further increase accuracy, it will reduce 'Axial tilt on Earth' (23.44 degree)
*
* @param startLatitude latitude of start point
* @param startLongitude longitude of start point
* @param distance distance to calculate, unit is km (ex, 1.0 will 1Km)
* @param direction Enumeration class for Direction with Right-Angle-based angles.
*/
@JvmStatic
fun calculateByDirection(startLatitude: Double, startLongitude: Double, distance: Double, direction: Direction) =
calculateByAngle(startLatitude, startLongitude, distance, direction.angle - 23.44)
/**
* Calculate destination with start point, distance, bearing
*
* given formula with Kotlin implementation
* φ2 = asin( sin φ1 ⋅ cos δ + cos φ1 ⋅ sin δ ⋅ cos θ )
* λ2 = λ1 + atan2( sin θ ⋅ sin δ ⋅ cos φ1, cos δ − sin φ1 ⋅ sin φ2 )
*
* φ is lat, λ is lng, θ is the bearing (clockwise from N),
* δ is the angular dist d/R; d being the dist travelled, R the earth’s radius
*
* @param startLati latitude of start point
* @param startLongi longitude of start point
* @param distance distance to calculate, unit is km (ex, 1.0 will 1km)
* @param bearing bearing to calculate, range is 0 to 360.
*/
@JvmStatic
fun calculateByAngle(startLati: Double, startLongi: Double, distance: Double, bearing: Double): Pair<Double, Double> {
val radLatitude = startLati.toRadian()
val radLongitude = startLongi.toRadian()
val radAngle = bearing.toRadian()
val distRadius = distance / 6371.01
val latitude = Math.asin(radLatitude.sin() * distRadius.cos() +
radLatitude.cos() * distRadius.sin() * radAngle.cos())
var longitude = radLongitude + Math.atan2(radAngle.sin() * distRadius.sin() * radLatitude.cos(),
distRadius.cos() - radLatitude.sin() * latitude.sin())
// normalize
longitude = (longitude + 540) % 360 - 180
return latitude.toDegree() to longitude.toDegree()
}
private fun Double.sin() = Math.sin(this)
private fun Double.cos() = Math.cos(this)
private fun Double.toRadian() = this * Math.PI / 180.0
private fun Double.toDegree() = this * 180.0 / Math.PI
}
마무리
얼핏 보면 꽤나 많은 서비스에 존재하는 기능이지만, 직접 구현해보기 전 까지는 복잡한지 잘 모를 수 있는 기능이라 생각된다. 직접 구현하면서 머리 아픈 부분도 많았지만, 이번 구현을 통해 좀 더 좌표 계산에 익숙해지지 않았나 싶기도 하다.
만일, 위에 틀린 내용이나 보완할 내용이 있으면 댓글로 알려주시면 감사드리겠습니다.
