[Programmers] 후보키 / python

문제

후보키

프렌즈대학교 컴퓨터공학과 조교인 제이지는 네오 학과장님의 지시로, 학생들의 인적사항을 정리하는 업무를 담당하게 되었다.

그의 학부 시절 프로그래밍 경험을 되살려, 모든 인적사항을 데이터베이스에 넣기로 하였고, 이를 위해 정리를 하던 중에 후보키(Candidate Key)에 대한 고민이 필요하게 되었다.

후보키에 대한 내용이 잘 기억나지 않던 제이지는, 정확한 내용을 파악하기 위해 데이터베이스 관련 서적을 확인하여 아래와 같은 내용을 확인하였다.

• 관계 데이터베이스에서 릴레이션(Relation)의 튜플(Tuple)을 유일하게 식별할 수 있는 속성(Attribute) 또는 속성의 집합 중, 다음 두 성질을 만족하는 것을 후보 키(Candidate Key)라고 한다.
  - 유일성(uniqueness) : 릴레이션에 있는 모든 튜플에 대해 유일하게 식별되어야 한다.
  - 최소성(minimality) : 유일성을 가진 키를 구성하는 속성(Attribute) 중 하나라도 제외하는 경우 유일성이 깨지는 것을 의미한다. 즉, 릴레이션의 모든 튜플을 유일하게 식별하는 데 꼭 필요한 속성들로만 구성되어야 한다.
  

제이지를 위해, 아래와 같은 학생들의 인적사항이 주어졌을 때, 후보 키의 최대 개수를 구하라.

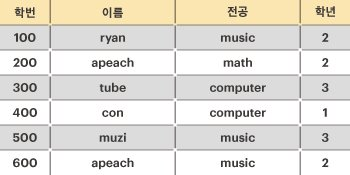
위의 예를 설명하면, 학생의 인적사항 릴레이션에서 모든 학생은 각자 유일한 학번을 가지고 있다. 따라서 학번은 릴레이션의 후보 키가 될 수 있다.
그다음 이름에 대해서는 같은 이름(apeach)을 사용하는 학생이 있기 때문에, 이름은 후보 키가 될 수 없다. 그러나, 만약 [이름, 전공]을 함께 사용한다면 릴레이션의 모든 튜플을 유일하게 식별 가능하므로 후보 키가 될 수 있게 된다.
물론 [이름, 전공, 학년]을 함께 사용해도 릴레이션의 모든 튜플을 유일하게 식별할 수 있지만, 최소성을 만족하지 못하기 때문에 후보 키가 될 수 없다.
따라서, 위의 학생 인적사항의 후보키는 학번, [이름, 전공] 두 개가 된다.

릴레이션을 나타내는 문자열 배열 relation이 매개변수로 주어질 때, 이 릴레이션에서 후보 키의 개수를 return 하도록 solution 함수를 완성하라.

제한사항

• relation은 2차원 문자열 배열이다.
• relation의 컬럼(column)의 길이는 1 이상 8 이하이며, 각각의 컬럼은 릴레이션의 속성을 나타낸다.
• relation의 로우(row)의 길이는 1 이상 20 이하이며, 각각의 로우는 릴레이션의 튜플을 나타낸다.
• relation의 모든 문자열의 길이는 1 이상 8 이하이며, 알파벳 소문자와 숫자로만 이루어져 있다.
• relation의 모든 튜플은 유일하게 식별 가능하다.(즉, 중복되는 튜플은 없다.)

🤔 생각

• 처음 보고 combinations 제너레이터를 연속 호출해서 부분 집합을 만들고, 유일성 최소성을 비교하면 되겠다고 생각했다.

• 뭐 로직이 안 떠올랐던건 아니다. 그런데...

• 최소성 검사 부분에서 다소 코드가 거북해질것 같았다.

• 집합 길이를 계속 비교하게 될것 같은데, 시간복잡도가 꽤 말썽일거다.

생각해보니 결국은 부분집합을 구하는 문제 아니던가.
비트마스킹으로 아예 집합을 정수형으로 표현해버린다면? 시간 복잡도는 물론 메모리도 크게 절약된다.
최소성 검사도 단순 AND 연산 하나로 처리가 끝난다. 비트마스킹으로 풀어보자!

📌 내 풀이

def checkuniq(arr, row):
    return True if len(set(zip(*arr))) == row else False
    
    
def checkmin(num, unique):
    for i in unique:
        if i & num == i: return False
    return True


def solution(relation):
    relation = tuple(zip(*relation))
    col = len(relation)
    row = len(relation[0])
    candidate = []
    
    for num in range(1, 1 << col):
        tmp = tuple(relation[i] for i in range(col) if num & (1 << i))
                
        if checkuniq(tmp, row) and checkmin(num, candidate):
            candidate.append(num)
            
    return len(candidate)

✔ 회고

• 처음엔 다소 어렵게 느껴진 문제였다.
• 그러나 이진수를 하나의 부분집합의 표현으로 생각하는 습관을 들인다면, 아주 쉬워지는 문제였다!
• 부분집합을 표현할 땐 비트마스크를 고려해보자.