DailyCoding
- 첫 글자가 대문자인 문자열을 리턴하시오.
public class LetterCapitalize {
public String letterCapitalize(String str) {
if(str=="") return str;
// while(str.contains(" ")){ // 중복된 공백 제거
// str = str.replaceAll(" ", " "); // 공백 2개를 1개로 바꾸기
// }
String result = "";
String[] strChange1 = str.split("\\s"); // 띄어쓰기 기준으로 단어 분리, 배열로 저장
String strChange2 = "";
for(int i=0; i<strChange1.length; i++){ // 단어 하나씩 반복문 실행
//strChange1[i] = strChange1[i].replace(" ", ""); // i번째 단어에 공백 남아있으면 공백 제거 trim()써도 됨. //공백기준으로 split 했기 때문에 빈배열 자체가 하나의 배열요소로 들어갔다.
if(strChange1[i].equals("")){ //공백은 그대로 공백 출력하게 나눠주기
strChange2 = strChange1[i];
}else{
strChange2 = strChange1[i].substring(0, 1).toUpperCase() + strChange1[i].substring(1);
}
if (result == "") result = strChange2;
else result = result + " " + strChange2; //String.join쓰면 조금 더 간단히 가능
}
return result;
}
}공백은 단어 사이를 구분하는 용도로만 쓰이는 줄 알고 중복된 공백을 제거하는 등 잘못된 방향으로 접근했었다.
공백간격도 그대로 유지해야 하기 때문에 위와 같이 코드를 작성해
공백이 두칸 이상일 때 split으로 인해 빈배열이 하나 추가되어 공백을 추가해주는데 사용할 수 있었다.
Section2 - 코딩테스트 준비
의사코드(pseudocode)
의사코드 사용의 장점
- 시간단축
- 디버깅에 용이함
- 사용한 프로그래밍 언어를 모르는 사람도 이해, 소통 가능
자신만의 원칙을 만들어, 일관성이 있으며 다른 사람도 이해할 수 있는 수도코드를 작성하도록 하자.
시간복잡도(Time Complexity)
입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 걸리는 정도
Big-O 표기법
입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마나 걸리는지 표기하는 방법
시간 복잡도 표기하는 방법
- Big-O(빅-오)
- Big-Ω(빅-오메가)
- Big-θ(빅-세타)
위와 같이 3가지 방법이 있지만 주로 Big-O 사용
- O(1) (= constant complexity)
- 입력값에 상관없이 즉시 출력
- ex.
int a = 9999,sout(a)
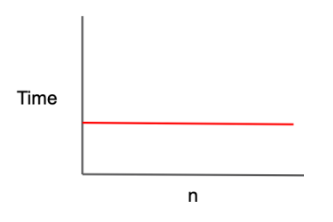
- O(n) (= linear complexity)
- 입력값의 증가에 따라 출력시간도 같은 비율로 증가
- ex. for문
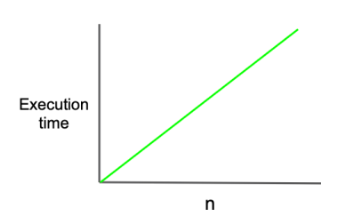
-
O(log n) (= logarithmic complexity)
- 입력값의 증가에 따라 출력시간 증가비율 감소
- ex. BST (탐색할수록 경우의 수가 줄어든다)
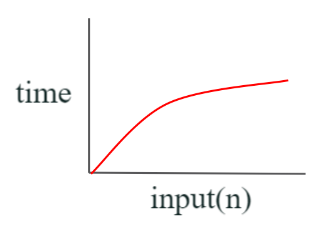
-
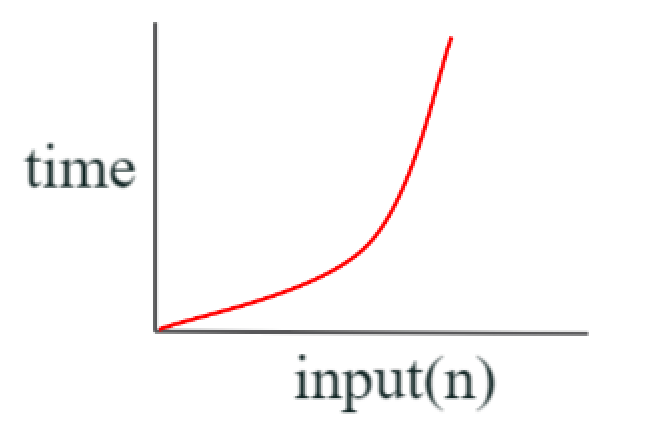
O(n^2) (= quadratic complexity)
- 입력값의 증가에 따라 출력시간이 n의 제곱수의 비율로 증가
- ex. 2중for문
-
O(2^n) (= exponential complexity)
- 입력값이 증가하면 출력시간이 2배로 증가
- ex. 재귀+재귀
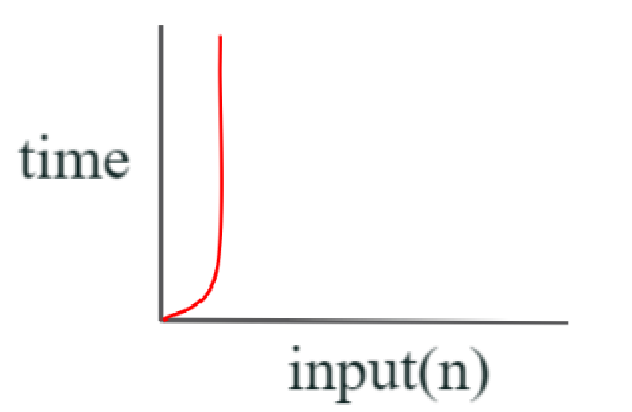
total시간은 고정되어 있는데 입력값이 크면 효율 좋은 시간 복잡도를 선택해야 겠다고 아래처럼 추정이 가능하다.
| 데이터 크기 제한 | 예상되는 시간복잡도 |
|---|---|
| n<=1,000,000 | O(n) or O(logn) |
| n<=10,000 | O(n^2) |
| n<=500 | O(n^3) |
시간복잡도 quiz 오답정리
4번
n ≥ 10,000일 때, 가장 느린(&&빠른) 시간 복잡도를 가지는 알고리즘의 Big-O 타입은? (문제 보기에서 O(1)은 없다)
(O(n), O(2n), O(log n), O(n2), O(n!) 중 택2)
나의 오답
- 가장 빠른 Big-O = O(n)
- 가장 느린 Gig-O = O(n!)
정답
- 빠른 Big-O = O(log n)
- 느린 Gig-O = O(n!)
O(log n)이 n==1 을 제외하고 O(n)보다 빠르다.
6번
int a = 0,
int b = 0;
for (i = 1; i < n; i+=1) {
a = a + 1;
}
for (j = 2; j < n; j+=1) {
b = b + 1;
}위 코드의 시간 복잡도를 Big-O로 표시한 것은?
나의 오답
- O(2n)
정답
- O(n)
for문이 2개라... 2n인줄 알았다.
같은 비율로 증가하고 있다면 5배건 10배건 O(n)으로 표기한다.
(O(1)인 알고리즘을 생각해보자. 단순 출력을 n번한다고 O(n)이라 표기하지 않는다)
9번
for (int i = 0; i < n; i++) {
i *= k;
}위 코드의 시간 복잡도를 Big-O 표기법으로 나타내시오.
나의 오답
- O(log n)
정답
- O(log n)
- O(log k n)
log base는 big O notation에서 중요하지 않기때문에 log n이 정답이지만 수학적으로 log(basek)n === time 꼴로 k배수만큼 i가 커지며 n에 도달하기 때문에 O(log k n)도 정답이다.
Q: 근데 그렇게 치면 6번 문제도 수학적으로 따지면 2n 아닌가??..
A:
알고리즘
Greedy(탐욕 알고리즘)
선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에 도달하는 방법
(항상 최적의 결과를 도출하는 것은 아니지만, 어느 정도 최적에 근사한 값을 빠르게 도출할 수 있는 장점이 있다.)
-
- 선택 절차(Selection Procedure): 현재의 상황에서 최적의 해답을 선택
-
- 적절성 검사(Feasibility Check): 선택된 해가 문제의 조건을 만족하는지 검사
-
- 해답 검사(Solution Check): 문제가 해결되었는지 검사하고, 해결되지 않았다면 1번으로 돌아가 반복
탐욕 알고리즘은 현재의 상황에서 최선의 판단을 하기 때문에 상황이 바뀔 수 있는 경우에는 최적의 해를 구할 수 없다.
따라서, 아래의 조건들을 만족할 때 사용해야 한다.
탐욕 알고리즘 적용 조건
-
탐욕적 선택 속성(Greedy Choice Property)
: 앞의 선택이 이후의 선택에 영향을 주지 않는다. -
최적 부분 구조(Optimal Substructure)
: 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법과 같은 방법으로 구성된다.
완전 탐색 알고리즘(Brute-Force Algorithm)
모든 가능성을 시도하여 문제를 해결하는 방법
완전 탐색(brute force) = 가능한 모든 경우의 수를 전부 확인하여 문제를 푸는 방식
- 최족의 솔루션 x
- 공간복잡도와 시간복잡도를 고려하지 않고 최악의 방법이라도 솔루션 찾기에 집중하는 방법
- 데이터 범위가 커질수록 비효율적
- 문제의 복잡도에 매우 민감
- 컴퓨터 성능에 기대는 방법
BFA 사용하는 경우
- 프로세스 속도를 높이는데 사용할 수 있는 다른 알고리즘이 없을 때
- 문제를 해결하는 여러 솔루션이 있고 각 솔루션을 확인해야 할 때
예시,종류
- 순차 검색 알고리즘 (Sequential Search)
- 배열 0번인덱스~끝번인덱스 까지 다 찾는 것 등
- 문열 매칭 알고리즘 (Brute-Force String Matching)
- 문자열에서 특정 문자열을 포함하는지 검사하는 알고리즘
- 선택 정렬 알고리즘 (Selection Sort)
- 오름,내림차순으로 정렬하는 정렬알고리즘
- Tree 자료 구조의 완전탐색 알고리즘 - Exhausive Search (BFS, DFS)
이진 탐색 알고리즘(Binary Search Algorithm)
데이터가 정렬된 상태에서 절반씩 범위를 나눠 분할 정복기법으로 특정한 값을 찾아내는 알고리즘
앞서 정리한 BST와 비슷하지만 BST는 자료구조다! (다른거임)