| 퀵정렬 | 병합정렬 | 힙정렬 | |
|---|---|---|---|
| 특징 | 불안정, 제자리, 피벗 있는 분할정복 | 안정, 제자리, 원본크기 메모리 필요 | 불안정, 제자리, 트리 |
| 평균 | nlogn | nlogn | nlogn |
| 최악 | n^2 | nlogn | nlogn |
| 최선 | nlogn | nlogn | nlogn |
| 공간복잡도 | n | n | n |
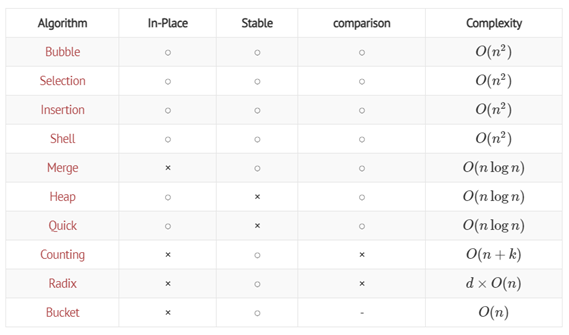
- in-place : 입력리스트 내부에서 정렬이 이뤄진다. 반대는 별도 저장공간을 필요로 하는 경우다.
- stable : 같은 원소의 자리가 정렬 이후 바뀔 수 있다.
퀵 정렬(Quick Sort)
-
구동방식
퀵 정렬(Quick Sort)은 기준값(Pivot)을 중심으로 자료를 왼쪽 부분집합과 오른쪽 부분집합으로 분할한다. 왼쪽 부분집합으로 기준값보다 작은 원소를 이동시키고, 오른쪽 부분집합으로 기준값보다 큰 원소를 이동시킨다. 퀵 정렬은 분할과 정복(Divide and Conquer)라는 작업을 반복하여 수행한다. -
시간복잡도
(1) 최선
피봇에 의한 원소들의 부분집합이 정확히 n/2개씩 2등분 되는 경우가 반복되는 경우
O(nlog2n)
(2) 최악
피봇에 의한 원소들의 부분집합이 1개과 n-1개로 분할되는 경우가 반복되는 경우
O(n^2) -
활용케이스
메모리가 부족하고(병합정렬 사용 불가)
배열이 이미 정렬/역정렬되어있을 가능성이 없고(퀵소트 최악의 경우)
동일한 요소의 자리가 바뀌어도 상관 없는 경우(not stable하므로)
퀵 정렬의 최악의 경우는, 기준 원소가 항상 유일한 최소 원소이거나 최대 원소일 경우이다. 즉, 정렬 또는 역순정렬되어있을 경우 정렬이 n-1번 수행되면서 최악의 경우가 발생한다. 퀵정렬은 not stable이기 때문에, 자리가 바뀌어서는 안 될 경우 in-place정렬을 사용해야 한다.
힙 정렬(Heap Sort)
-
구동방식
모든 노드가 힙 속성(각 노드의 값이 자신의 자식노드 값보다 큰 이진트리)을 만족하도록 재귀적으로 트리 구조를 만들어 정렬을 완성 -
시간복잡도
이상적인 경우에 퀵정렬과 비교했을 때 똑같이 O(n log n)이 나오긴 하지만 수행 시간은 퀵정렬보다 평균적으로 느리다. 즉, 데이터의 상태에 따라서 다른 정렬법들에 비해서 조금 느린 편이다. 또한, 안정성(Stable)을 보장받지 못한다는 단점이 있다. -
활용케이스
메모리가 부족하고(병합정렬 사용 불가)
배열이 이미 정렬/역정렬되어있을 가능성이 있고(퀵정렬 사용 불가)
같은 원소의 원래 위치가 바뀌어도 상관 없는 경우(힙정렬은 불안정 정렬이므로)
메모리 측면에서 효율적입니다. 또한 항상 O(N * log N)을 보장할 수 있다는 점이 좋습니다. 하지만 단순히 속도만 가지고 비교하면 퀵 정렬이 평균적으로 더 빠릅니다.
병합정렬(Merge Sort)
-
구동방식
리스트를 잘게 쪼갠 뒤 둘씩 크기를 비교해 정렬하고 분리된 리스트를 재귀적으로 합쳐서 정렬을 완성, 분할된 리스트를 저장해둘 공간이 필요해 메모리 소모량이 큰 편이다. -
시간복잡도
분할과정은 매번 반씩 감소하므로 밑이 2인 O(log n)만큼 반복해야 크기가 1인 배열로 분할 할 수 있다. -
활용케이스
배열이 이미 정렬되어있을 가능성이 있으며, 메모리가 충분한 경우
퀵정렬과 달리 Pivot이 없으므로 성능이 저하 없이 항상 O(n log n)이다.
병합 정렬은 순차적인 비교를 통해 정렬하므로, LinkedList의 정렬에 효율적이다.
병합정렬은 추가 메모리를 요구하므로, 메모리 효율이 중요한 경우 퀵정렬이 나을 것이다.
보너스