1. 문제

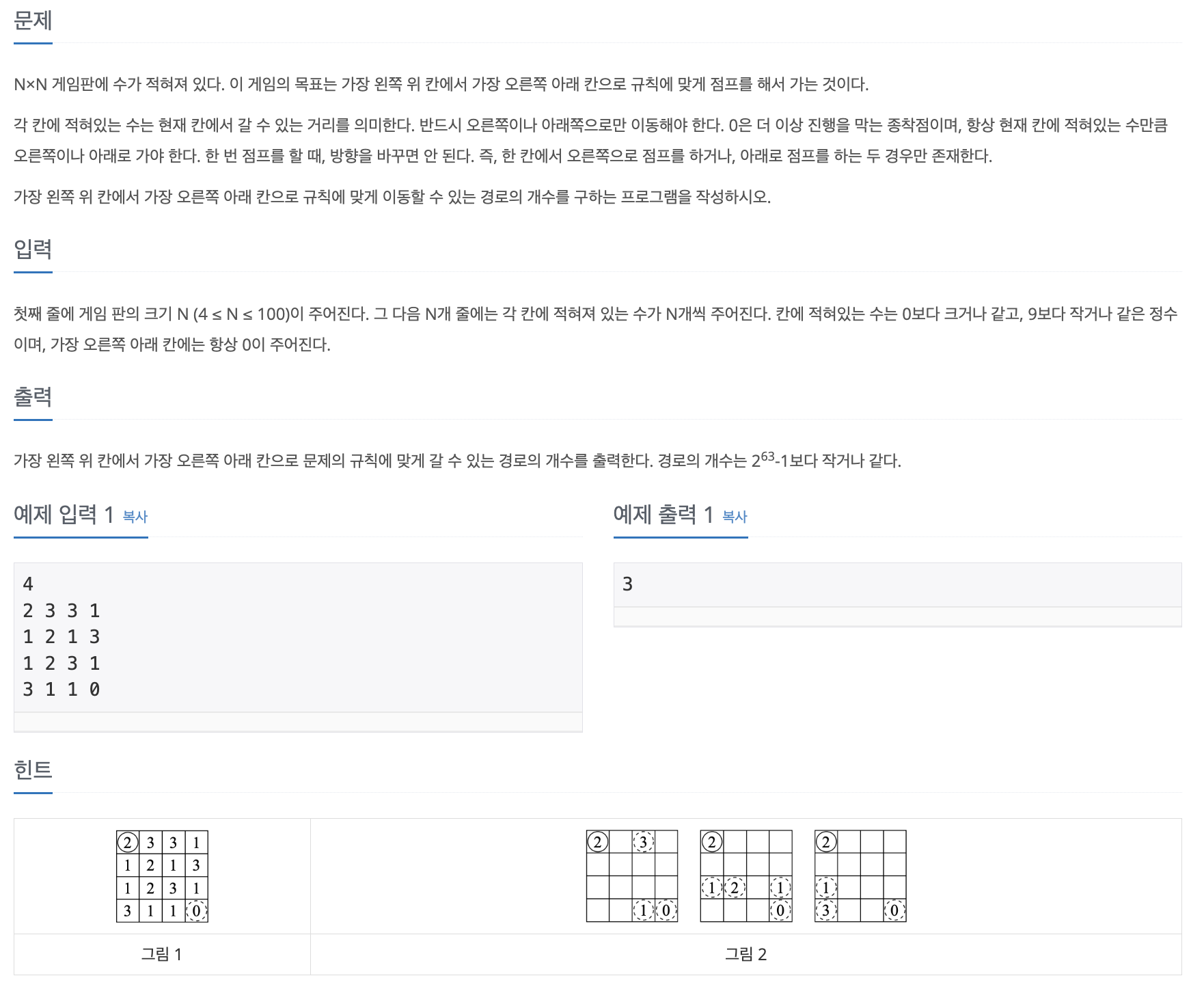
2. 코드

import java.util.Scanner;

public class Main {
    static int n;

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        Scanner s = new Scanner(System.in);

        n= s.nextInt(); // 게임판의 크기
        int list[][] = new int[n+1][n+1];
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=n;j++) {
                list[i][j] = s.nextInt();
            }
        }

        long dp[][] = new long[n+1][n+1]; // 경로의 개수는 2^63-1보다 작거나 같으니 long타입
        dp[1][1]=1;

        for(int i=1;i<=n;i++) {
            for(int j=1;j<=n;j++) {
                int next = list[i][j];
                if(i==n&&j==n) {
                continue;
                }
                if(j+next<=n) {
                dp[i][j+next] += dp[i][j];
                }
                if(i+next<=n) {
                dp[i+next][j] += dp[i][j];
                }
            }

            // dp 변화 출력확인
            //print(dp);
            //System.out.println();
        }
        System.out.println(dp[n][n]);
    }
    public static void print(long[][] dp){
        for(int i=1; i<=n; i++){
            for(int j=1; j<=n; j++){
                System.out.print(dp[i][j]+" ");
            }
            System.out.println();
        }

    }
}

3. 풀이

• DFS와 다이나믹 프로그래밍으로 풀 수 있는 문제이다.

• 답이 263 - 1 로 매우 큰 수이기때문에 DFS로 하다가는 중복된 구간을 계속 방문하게 되어, 필연적으로 시간초과가 발생한다. 따라서 long[][] 타입의 dp를 정의하여 메모이제이션을 수행해야한다.

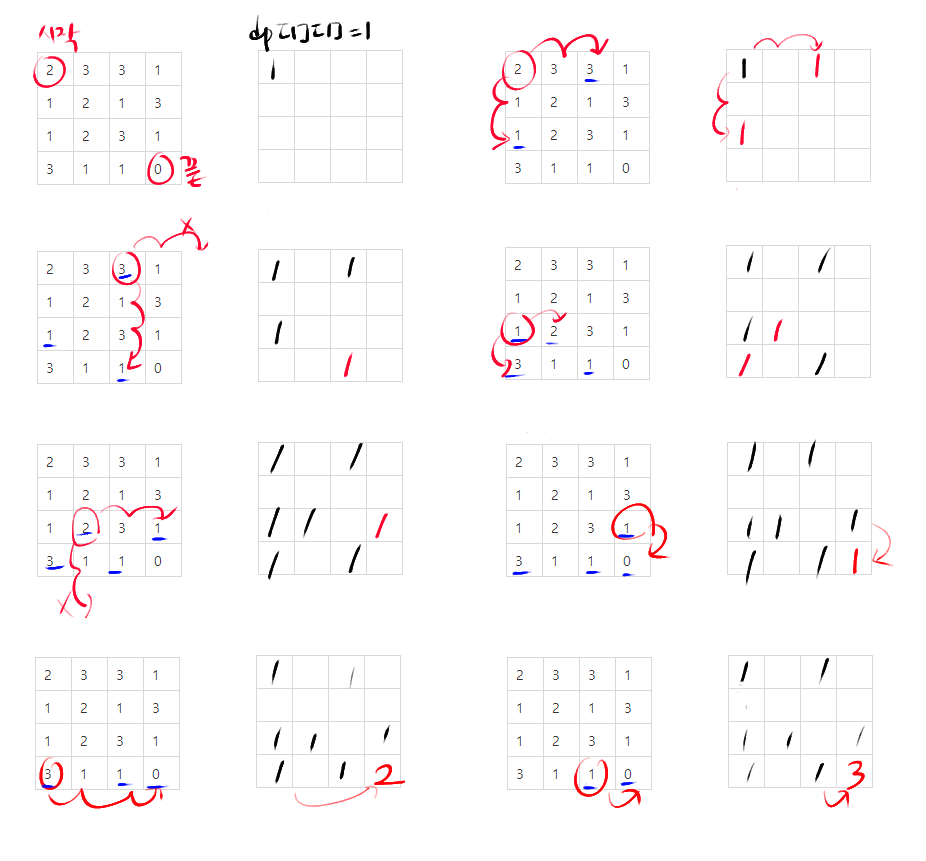
• 게임판에 적혀있는 정수들의 배열을 list[][], 그 칸에 도착하게되는 경로의 개수를 dp[][]라고 하면, 각 칸에 적혀져 있는 수만큼 오른쪽 or 아래방향으로 움직이게 되니까, list[i][j]에서의 다음 이동 칸은 list[i+list[i][j]][j] 또는 list[i]j+list[i][j]], 이 두가지 경우가 될 수 있다.

• 즉, 다음으로 도착하게 되는 이동칸에 이전 칸까지 오는 경로의 개수를 더해주면 된다.

• dp[i+list[i][j]][j] += dp[i][j], dp[i]j+list[i][j]] += dp[i][j] 인 셈이다.

• 이 때, i+list[i][j] 와 j+list[i][j]는 N보다 같거나 작은 범위에서만 가능하다.

• 왼쪽이 게임판인 list, 오른쪽이 경로의 개수를 더하는 dp이다.

4. 링크

https://www.acmicpc.net/problem/1890
https://hu-coding.tistory.com/36