1. 그리디 알고리즘 (Greedy Algorithm)
-
그리디 알고리즘이란, 말 그대로 greedy, 즉 탐욕 알고리즘이다. 그리디 알고리즘에서 가장 중요한 키워드는 '매 번의 선택에서 가장 좋아보이는 선택을 하여 적절한 답을 찾아간다'는 것이다.
-
서울에서 출발하여 부산을 가려 한다고 할 때, 다음 사진과 같이 경로들이 있고 각 경로에 따른 소요 시간이 적혀있다.
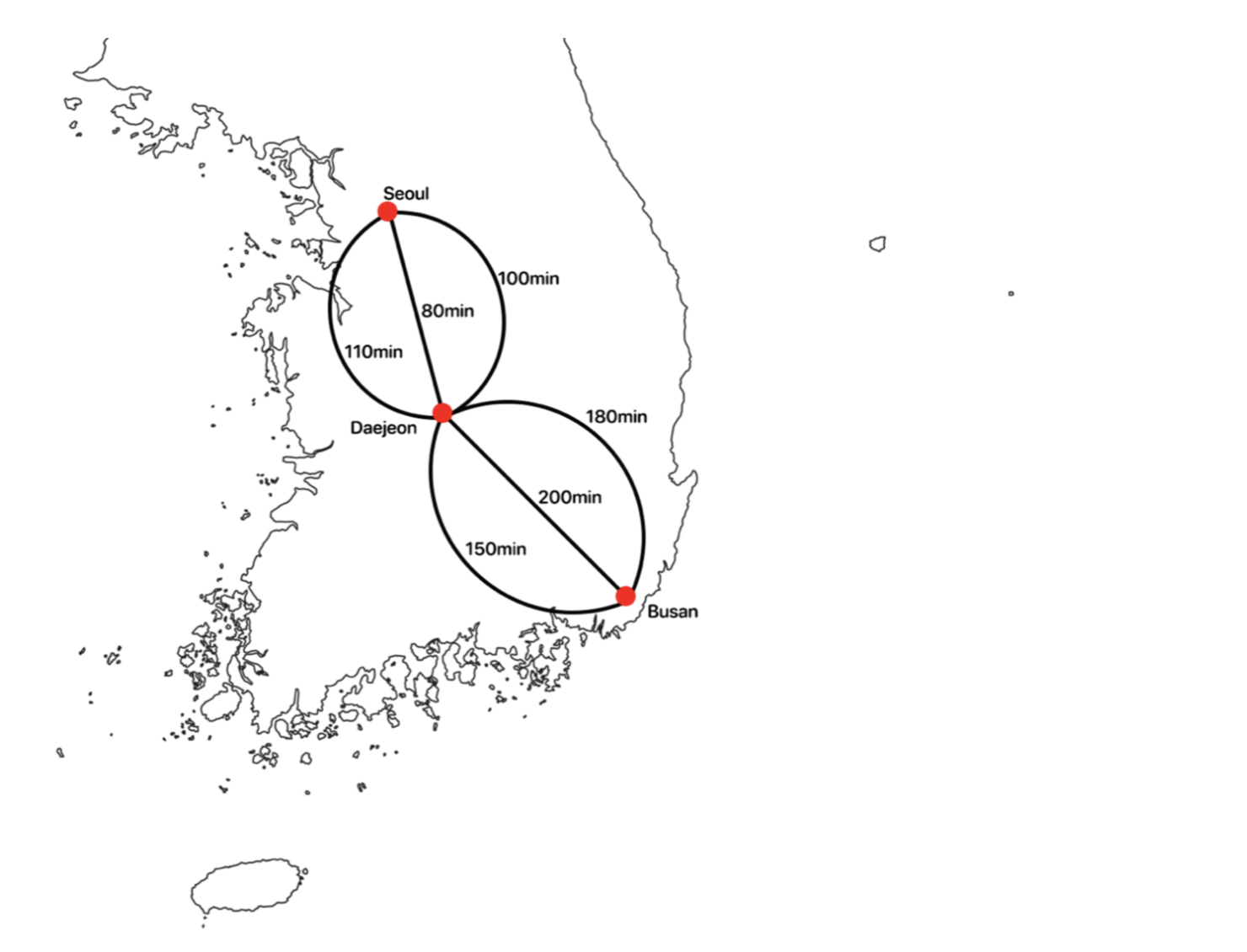
- 최대한 빠르게 서울에서 부산까지 가고싶을 때 경로는 ?
- 먼저 서울에서 대전을 가는 경로는 3개가 있다. 이 중 가장 적게 소요되는 경로의 경우 80분이 걸린다고 한다. 당연 빠르게 가려면 80분짜리 경로를 선택 할 것이다.
- 그 다음 대전에서 부산으로 가는 경로도 3개가 있다. 이 세 개중 150분이 걸리는 경로가 가장 시간이 적게 소요된다. 즉, 전체 루트로는 서울-대전 : 80분, 대전-부산 : 150분이라는 시간으로 총 230분(3시간 50분)이 걸린다.
- 이렇게 '각 단계별로 최선의 선택지를 선택'하는 것이 바로 그리디 알고리즘이다.
- 이 알고리즘은 꽤 좋아보이지만 여러분이 명심해야 할 것은 '그리디 알고리즘은 항상 최적의 해를 도출해내는 것은 아니다.'라는 것이다. 위 지도에서 새로 도로가 건설되어 다음과 같은 루트가 새로 생겼다고 해보자.
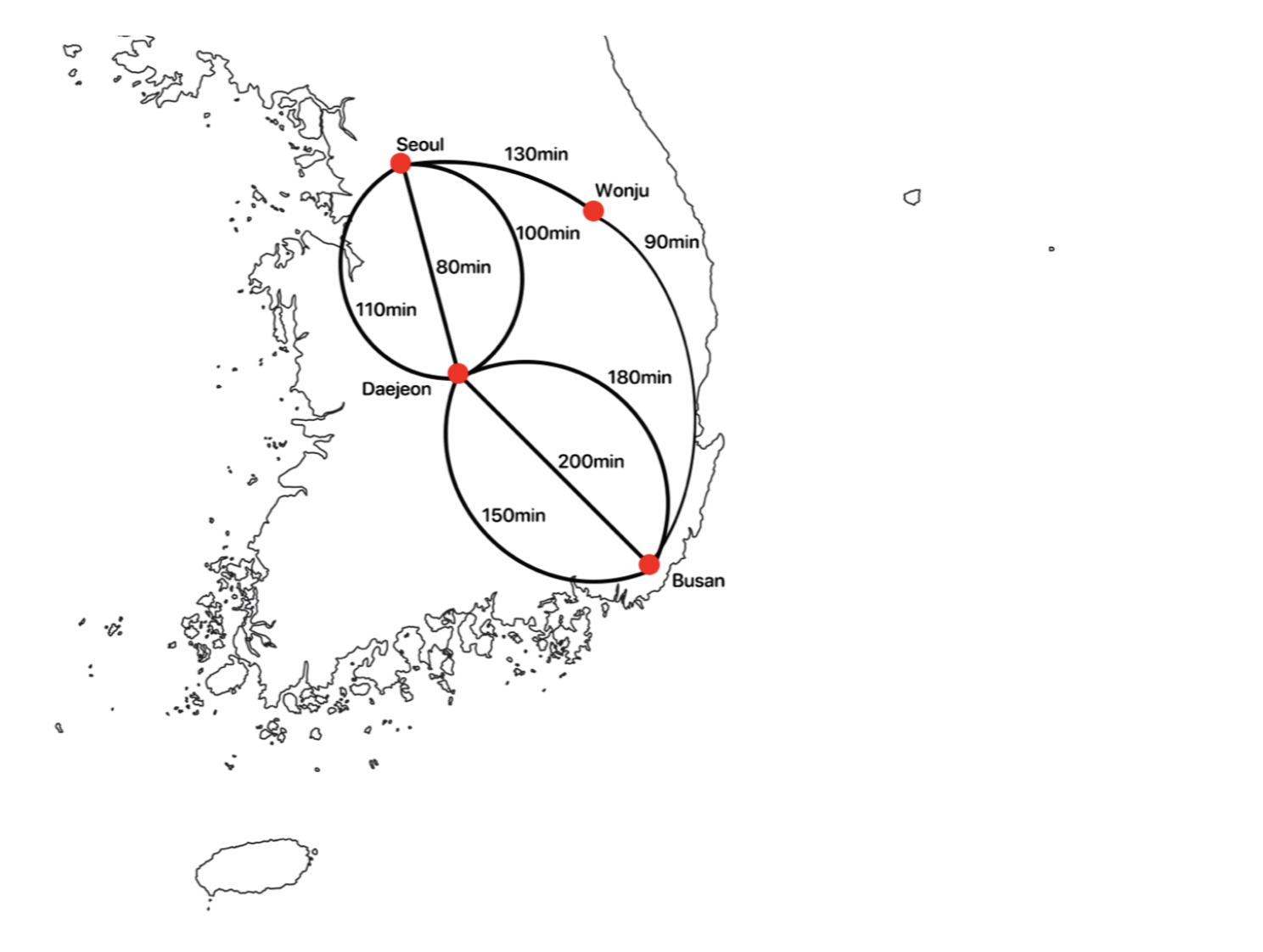
-
만약 그리디 알고리즘대로 한다면 각 순간 별 최적의 선택을 해야하니, 서울에서 이동하는 경로 중 가장 적게소요되는 '대전으로 가는 80분짜리 경로'를 선택한 뒤, 대전에서 부산으로 가는 경로 중 가장 적게 소요되는 '150분짜리 경로'를 선택하게 될 것이다.
-
하지만, 실제로는 서울에서 원주를 거쳐 부산으로 가는 길이 130분 + 90분 = 220분(3시간 40분)으로 앞선 240분(3시간 50분)보다 더욱 빨리 도착할 수 있다.
-
이런식으로 그리디 알고리즘은 '최적해에 근사하는 방법'인 것일뿐 항상 최적해를 만족하는 것이 아니다.
-
그리디 알고리즘이 잘 활용 될 수 있는 문제들은 대개 특징이 있는데, 1)이전의 탐욕 선택이 이후의 선택에 영향을 주지 않는다(독립적)는 점과 2)전체 최적해가 부분 문제에 대해서도 최적해를 만족한다는 것이다.
-
첫 번째 이미지에서는 서울에서 부산으로 이어지는 경로는 서울-대전-부산 경로밖에 없다. 즉, 서울-대전과 대전-부산의 경로는 각 독립적이기 때문에 서울-대전 경로에서 어떤 것을 선택하느냐에 따라서 대전-부산 경로의 선택에 영향을 미치지 않는다. 즉, 일단 첫 번째 조건을 만족한다.
-
또한 각 도시별 경로는 독립적이기 때문에 결과적으로 서울-대전의 최적해는 곧 전체 최적해의 부분 문제가 되고, 대전-부산의 최적해 또한 마찬가지다. 즉, 각 부분 문제의 최적해는 전체 문제의 최적해이자, 반대로 말하면 전체 최적해가 부분 문제에 대해서도 최적해를 만족한다는 것이다.
-
두 번째 이미지에서는 그럼 왜 최적해를 만족하지 못할까?
-
일단 서울에서 부산을 가는 도중 두 가지 도시로 나뉜다. 서울-대전을 잇는 경로와 서울-원주를 잇는 경로로 나뉘게 된다. 그렇게 되면, 이후 선택지는 대전-부산 또는 원주-부산경로로 나뉘게 되는데, 이는 처음 선택했던 경로에 따라 결정할 수 있는 경로에 영향을 미치기 때문에 독립적이지 않게 된다. 결과적으로, 독립적이지 않다는 것은 전체 최적해에 대해 부분 문제 또한 독립적이지 않아 항상 최적해를 만족하지 않는다까지 이어질 수 있다.
- 물론 장점은 뚜렷하다. 동적계획법과 달리 최적해를 100% 보장해주진 못하지만 각 순간별 최적 선택을 하기 때문에 근사 해를 구하는 속도가 매우 빠르다는 것이다. 그래서 동적계획법과 그리디 알고리즘은 서로 상호보완하여 같이 쓰이기도 한다. 예로들어 위의 두 번째 지도 이미지보다 더욱 많은 경로들이 있을 때 일정 구간을 분기점으로 두고 그 안에서는 동적계획법을 통해 가장 빠른 루트를 구하여 가는 방식이 있다.
