[선형대수 기초] Chapter 2 적분

이번 시리즈는 도서 "통계학을 위한 선형대수"(박흥선)을 참고하였습니다.

[학습개요]

• 학습목적
• 변수변환
• 자코비안 행렬(Jacobian Matrix)

[학습목적]

이번 파트는 도서 "통계학을 위한 선형대수"(박흥선)의 적분과 관련된 파트에 대한 내용이지만 고등학교 수준의 적분을 제외하고 중요한 내용이 변수변환 뿐이라고 생각하여 적분이 아닌 사실상의 변수 변환에 대해 다룰 예정이다.

하지만 변수 변환 과정에서 등장하는 자코비안 행렬(Jacobian matrix)가 매우 중요한 개념이기 때문에 짧은 글이지만 집중해서 읽어주면 좋겠다.

[변수변환]

적분 과정에서 변수를 치환함으로써 적분을 간단하게 할 수 있다. 하지만 적분에서 변수를 치환한다는 것은 단순히 변수를 바꾸는 것만을 의미하진 않는데, 이는 적분을 수행하는 영역이 x축에서 u축으로 옮겨졌기 때문이며 이에 따라 보정이 필요하게 된다.

• 시작점 $x=a$에 대한 u값은 $a=g(u)$에 의해 $u=g^{-1}(a)$가 되고
• 종착점 $x=b$에 대한 u값은 $b=g(u)$에 의해 $u=g^{-1}(b)$가 된다.
• 또한 $x=g(u)$의 관계식으로부터 $dx=g'(u)du$라고 계산되므로,
  이를 종합하면 다음과 같이 나타낼 수 있다.

  $\int_a^b f(x)dx = \int_{g^{-1}(a)}^{g^{-1}(b)} f(g(u))\left\vert g'(u) \right\vert du$

여기서 $\left\vert g'(u) \right\vert$에 절대값을 취한 이유는 함수의 부호를 그대로 유지하면서 보정작용을 하기 위함이다. 이렇듯 변수를 변환할 때 보정작용을 하기 위해 곱해주는 $g'(u)$를 자코비안(Jacobian, 혹은 야코비안)이라고 한다.

또한, 다변량함수에서도 단변량함수와 마찬가지로 자코비안이 필요하다.
만일 $x=g(u,v), y=h(u,v)$라는 변환을 통해 $(x,y)$에서 정의된 영역 $R$이 $(u,v)$로 오면서 영역 $G$로 바뀐다면, 이에 대한 중적분은 다음과 같이 계산된다.

$\int\int_{R}f(x,y)dxdy = \int\int_{G}f(g(u,v),h(u,v))\left\vert J \right\vert dudv$

여기서 $J$는 자코비안 행렬(Jacobian Matrix)로,

$\begin{pmatrix} \frac{\partial x}{\partial u}&\frac{\partial x}{\partial v }\\ \frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}\end{pmatrix}$

가 되고, 자코비안은 그 행렬의 행렬식(determinant)을 통해 다음과 같이 계산된다.

$J(u,v) = det\begin{pmatrix} a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix} = a_{11}a_{22}-a_{12}a_{21}$

[자코비안(Jacobian) 행렬]

$J = \begin{pmatrix} \frac{\partial f_1}{\partial x_1}& \cdots &\frac{\partial f_1}{\partial x_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial f_m}{\partial x_1}&\cdots&\frac{\partial f_m}{\partial x_n}\end{pmatrix}$

자코비안 행렬은 위처럼 1차 미분계수로 이루어진 행렬이다.
여기서 자코비안 행렬이 1차 미분계수로 구성된다는 것에서 미소 영역에서의 선형변환이라는 의미를 가진다는 것을 파악할 수 있다.

즉, 결론부터 말하면 자코비안은 미소 영역에서 ‘비선형 변환’을 ‘선형 변환으로 근사’ 시킨 것인데, 말이 어렵지만 차근히 이해해보자

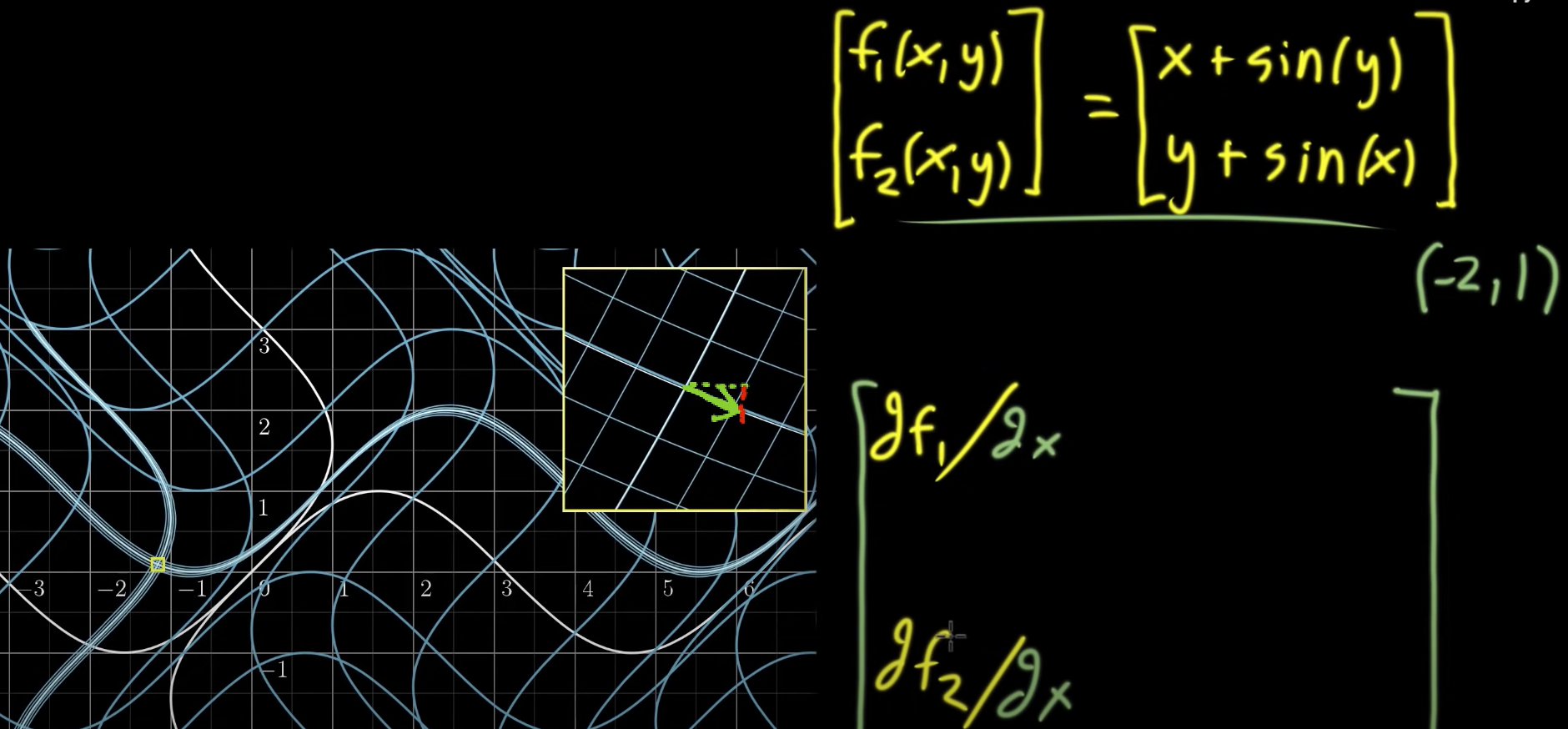
칸아카데미의 자코비안 강의에 따르면

으로 비선형변환을 하게 되더라도

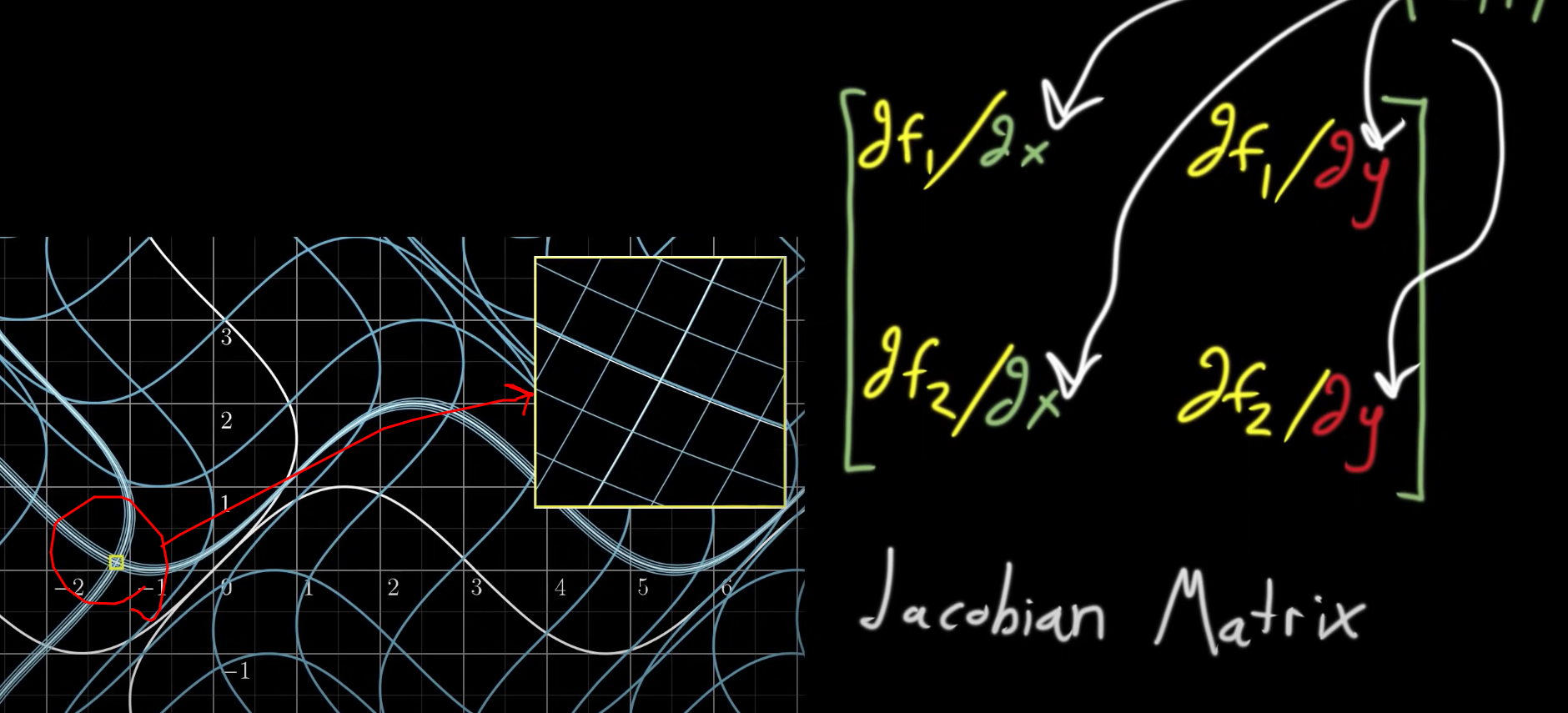
다음과 같이 미소 영역에서는 거의 선형과 비슷한 모습을 유지하게 된다.

이때 비선형 변환의 결과를 선형 변환과 유사하게 근사시켰을 때 $(u,v)$좌표계에서 $(x,y)$ 좌표계로 변한다고 한다면, 어떤 선형변환 $J$에 의해서 $du$와 $dv$는 $dx$와 $dy$로 변환된다고 볼 수 있다. 이를 수식으로 나타내면 다음과 같이 나타낼 수 있다.

위 수식을 풀어서 쓰면 다음과 같이 나타낼 수 있고,

위 두 수식을 다음과 같은 이변수 함수의 chain rule 공식에 적용한다면,

이변수 함수 $z=f(x,y)$에 대해 $x=g(t)$, $y=h(t)$이고, $f(x,y), g(t), h(t)$가 모두 미분가능한 함수일때

$\frac{dz}{dt}= \frac{\partial z}{\partial x}\frac{dx}{dt}+ \frac{\partial z}{\partial y}\frac{dy}{dt}$

이고, 이를 변형하면 다음과 같이 나타낸다.

$dz= \frac{\partial z}{\partial x}dx+ \frac{\partial z}{\partial y}dy$

국소적 비선형 변환의 전 후의 관계식을 얻을 수 있으므로, 자코비안 행렬은 다음과 같이 생각할 수 있다.

이를 통해 자코비안 행렬이 비선형 변환 등의 행렬의 변환에 따른 미소적인 부분에 대한 왜곡을 보완하는 기능을 수행함을 알 수 있고,
Jacobian의 행렬의 행렬식의 의미는 원래 좌표계에서 변환된 좌표계로 변환될 때의 넓이의 변화 비율을 말해준다는 것을 알 수 있다.

출처: https://angeloyeo.github.io/2020/07/24/Jacobian.html
https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/jacobian/v/the-jacobian-matrix