이분탐색(이진탐색)

이진탐색

이진 탐색이란 정렬된 배열에서 특정 값을 찾는 탐색 알고리즘이다.
이진 탐색은 배열의 중간을 기준으로 데이터를 탐색하기 때문에 반드시 데이터가 정렬된 상태로 존재해야 한다.

이진 탐색의 시간 복잡도는 O(logN)으로 배열을 전수 조사하는 O(N)에 비하면 상대적으로 빠른 탐색 알고리즘에 속한다. O(logN)만에 값을 찾을 수 있는 이유는 중간을 기준으로 탐색 대상을 절반씩 줄여나가기 때문이다.

이진탐색 : 개념

이진 탐색은 내가 찾고자 하는 값이 정렬된 배열의 중간 값보다 크면 중간값을 포함한 하위 값들은 탐색 대상에서 제외된다. 반대로 찾고자 하는 값이 배열의 중간 값보다 작으면 중간 값을 포함한 상위 값들은 탐색에서 제외된다.

정리하면 중간값과 찾으려는 값의 대소를 비교한 뒤 탐색 범위를 반으로 줄여가며 값을 찾는 탐색 알고리즘이다.

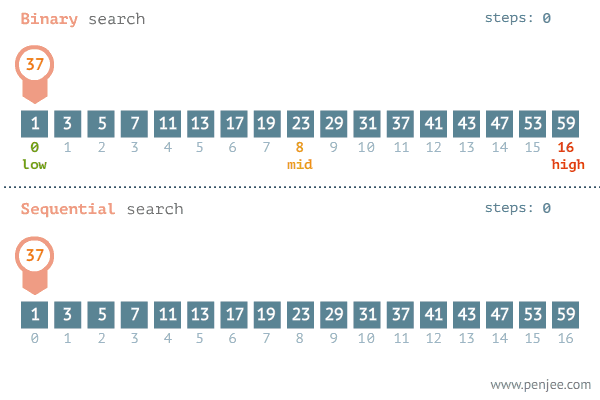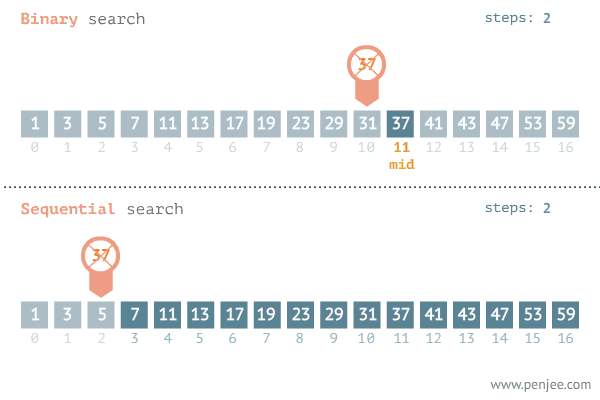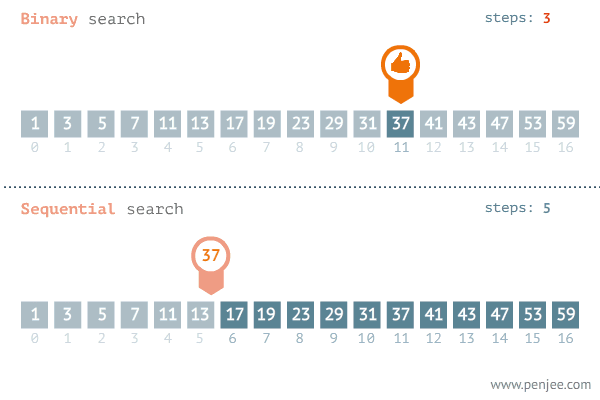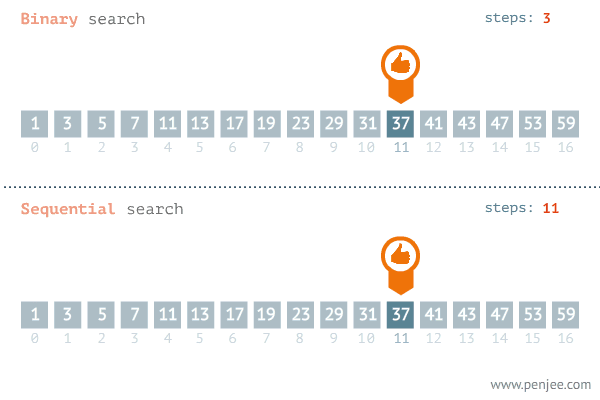
GIF출처 : https://blog.penjee.com/binary-vs-linear-search-animated-gifs/

이진탐색 : 코드

lt와 rt 그리고 mid 변수의 값을 변경하며 탐색의 범위를 줄여가는 것이 이진 탐색의 전부이다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main()
{
	int n, data, target, res = -1, lt = 0, rt, mid;
	vector<int> vec;

	cin >> n >> target;

	for (int i = 0; i < n; i++)
	{
		cin >> data;
		vec.push_back(data);
	}

	rt = n - 1;
	sort(vec.begin(), vec.end());

	while (lt <= rt)
	{
		mid = (lt + rt) / 2;

		if (vec[mid] == target)
		{
			res = mid;
			break;
		}
		else if (vec[mid] > target) rt = mid - 1;
		else if (vec[mid] < target) lt = mid + 1;
	}

	cout << "target index : " << res;
}

이진탐색 : 시간복잡도

운이 좋으면 찾고자 하는 값이 중간값과 동일해서 탐색이 끝나지만 최악의 경우 남은 데이터가 하나가 될 때까지 탐색을 반복한다. 이를 고려해 시간 복잡도를 계산해보자.

사진출처 : https://kangworld.tistory.com/65

---

💟 참고자료
이분 탐색과 시간복잡도