Binary Tree

Binary Tree는 비선형 자료 구조로 각각의 노드가 최대 2개의 자식 노드만을 가질 수 있습니다. 이 자식 노드들은 각각 left child 그리고 right child라고 불립니다.
Binary Tree에서 가장 위에 있는 노드를 root라고 부릅니다.
그리고 가장 아래에 있는 노드는 leavs라고 부릅니다.

Binary Tree 구성 요소

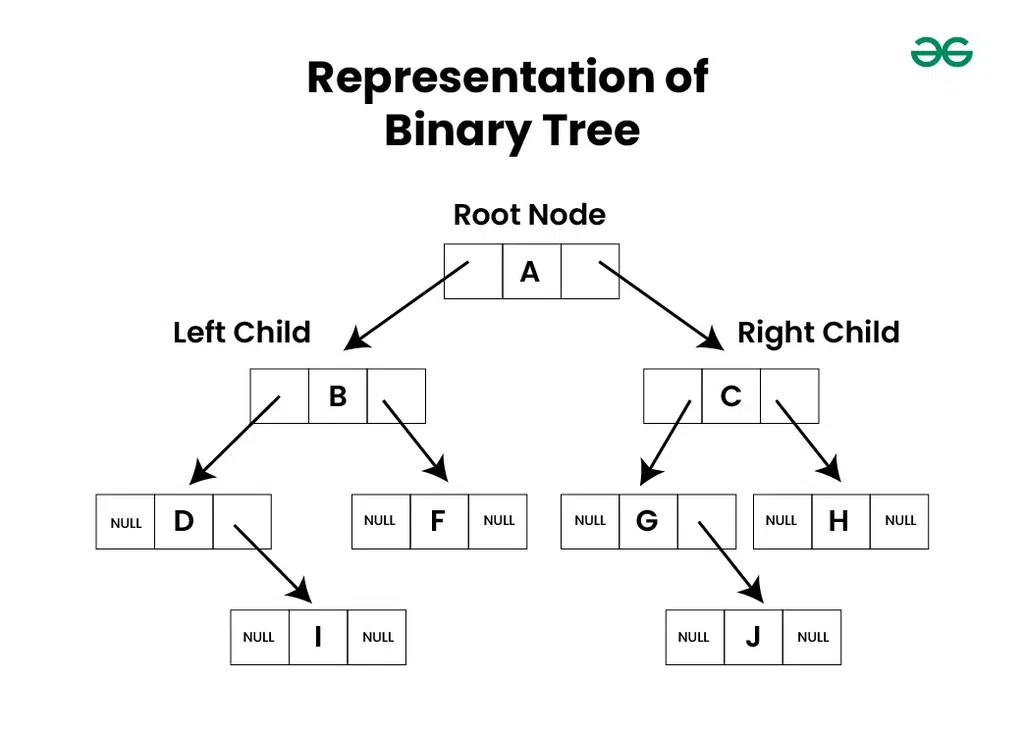
Binary Tree의 구성요소는 데이터와 왼쪽 자식을 가리키는 포인터, 오른쪽 자식을 가리키는 포인트로 이루어진 노드들의 집합입니다.

Binary Tree의 Operation

1. Insertion
   간단하게 Binary Tree에 값을 삽입하는 연산입니다.
   하지만 실제 Binary Tree에 값을 삽입하게 될 때는 여러 상황이 있고 이를 고려해서 만들어야 합니다.

• 왼쪽 자식이 없는 노드가 있는지 찾습니다. 만약 있다면 새로운 노드를 찾은 노드의 왼쪽 자식으로 넣습니다.
• 오른쪽 자식이 없는 노드가 있는지 찾습니다. 만약 있다면 새로운 노드를 찾은 노드의 오른쪽 자식으로 넣습니다.
• 만약 위의 조건에 부합한 노드를 찾지 못했다면 자식을 하나도 가지고 있지 않는 노드를 찾아 해당 노드의 왼쪽 자식이나 오른쪽 자식으로 새로운 노드를 넣습니다.

2. Traversal
   Traversal은 크게 두가지 유형으로 나뉩니다.
   Depth-First Search와 Breadth-First Search입니다.

Depth-First Search에는 Preorder Traversal, Inorder Traveral, Postorder Traversal이 있습니다.

• Preorder Traversal
  root -> left child -> right child 순으로 tree를 순회합니다.

• Inorder Traversal
  left child -> root -> right child 순으로 tree를 순회합니다.

• Postorder Traversal
  left child -> right child -> rott 순으로 treee를 순회합니다.

Breadth-First Search에는 Level Order Traversal이 있습니다.

• Level Order Traversal
  트리의 Level 순으로 순회합니다.

3. Deletion

• 삭제하고자 하는 노드의 자식이 존재하지 않는다면 그냥 삭제합니다.
• 삭제하고자 하는 노드가 자식을 가지고 있다면 자식이 없는 노드를 찾은 뒤 이 노드들을 서로 바꾸고 삭제합니다.

4. Searching
   traversal을 이용하여 tree를 순회하면서 찾고자 하는 값을 만나면 해당 노드를 반환하고 만약 tree를 모두 순회했는데도 찾고자 하는 값을 못 만났다면 해당 값이 존재하지 않음을 알리는 값을 반환합니다.

Binary Tree의 이점

• 효율적인 검색
• tree중에서는 효율적인 메모리 사용
• tree중 구현하기 쉬움

Binary Tree의 단점

• 제한된 구조
• 균형이 잡히지 않는다면 비효율적으로 변함
• 다른 자료 구조에 비해 비효율적
• 최악의 시나리오에서 너무 느림