Graph
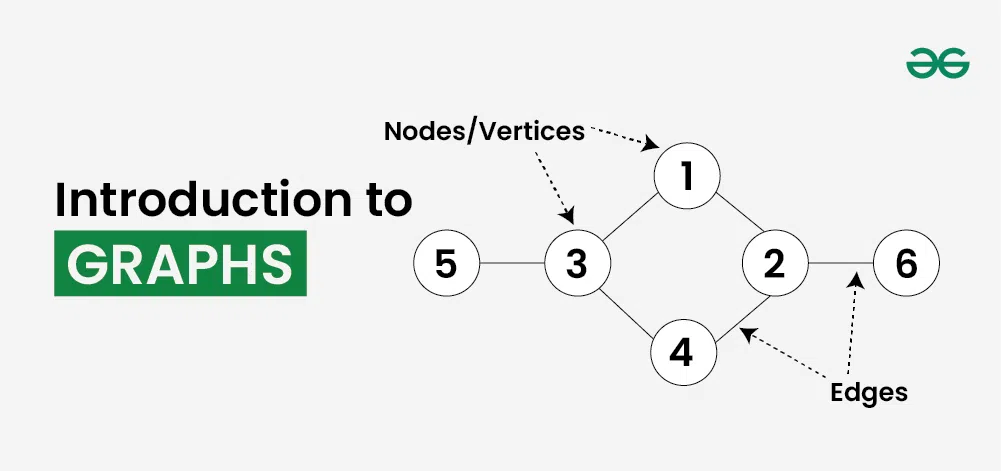
Graph는 비선형 자료구조로 vertices와 edges로 구성되어 있습니다.
이 자료는 소셜 네트워크 분석과 같이 네트워크 형태를 표현하는데 적합합니다.
Graph의 요소
-
Vertices
그래프의 주요 유닛입니다.
노드라고도 합니다.
각 Vertex는 라벨이 붙거나 안 붙을 수 있습니다. -
Edges
Edges는 두 개의 노드를 연결하기 위해 사용됩니다.
edge또한 라벨이 붙거나 안 붙을 수 있습니다.
Graph의 유형
-
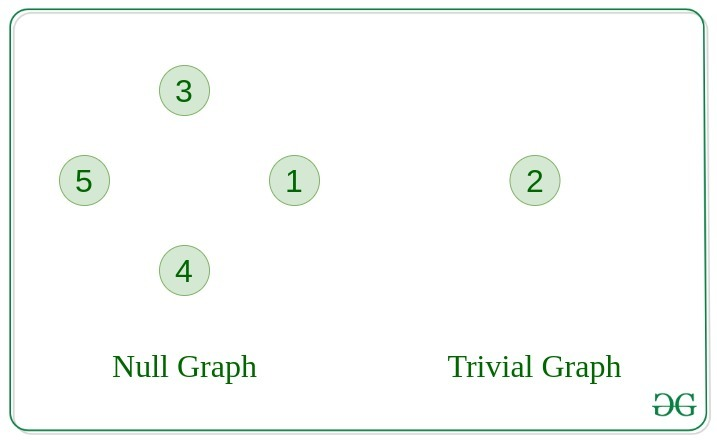
Null Graph
그래프에 간선이 없고 노드만 있다면 Null Graph라 합니다. -
Trivial Graph
하나의 노드만 가지고 있다면 이는 그래프가 가질 수 있는 가장 작은 형태이고 이를 Trivial Graph라고 합니다.
-
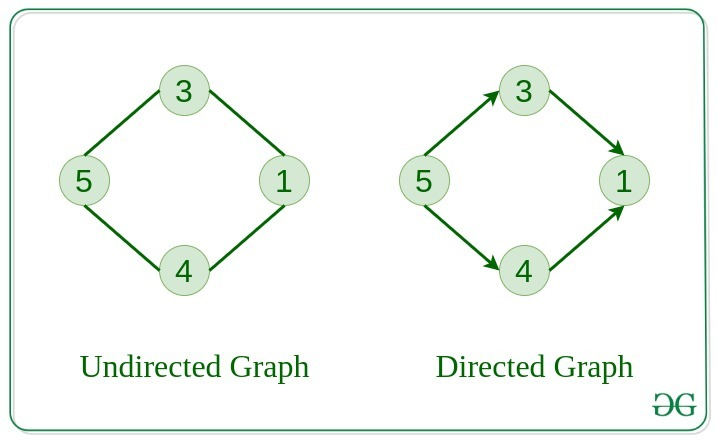
Undirected Graph
간선이 방향성을 가지지 않는 그래프를 무방향 그래프라고 합니다. -
Directed Graph
간선이 방향성을 가지고 있다면 방향 그래프라고 합니다.
-
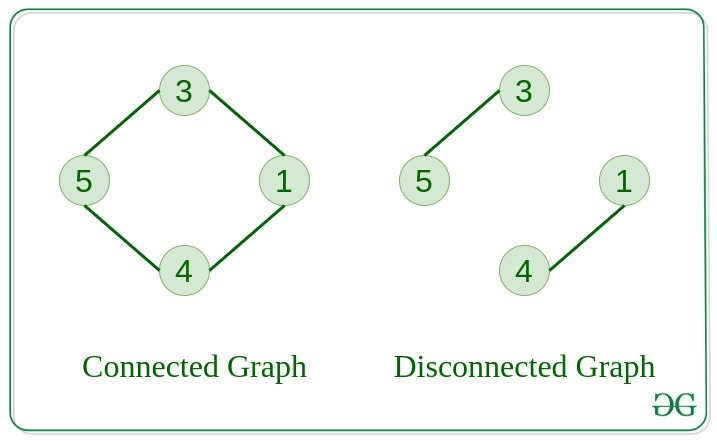
Connected Graph
연결 그래프는 아무 노드나 하나를 잡고 다른 노드에 연결된 간선을 통해 도달할 수 있는 그래프를 말합니다. -
Disconnected Graph
비연결 그래프는 특정 노드가 다른 특정 노드에 간선을 통해 도달할 수 없는 경우를 가진 그래프를 말합니다.
-
Regular Graph
정규 그래프는 모든 노드가 같은 수의 간선을 가지고 있는 그래프를 말합니다. -
Complete Graph
완전 그래프는 모든 노드가 자신을 제외한 다른 모든 노드에 간선을 통해 연결된 그래프를 말합니다.
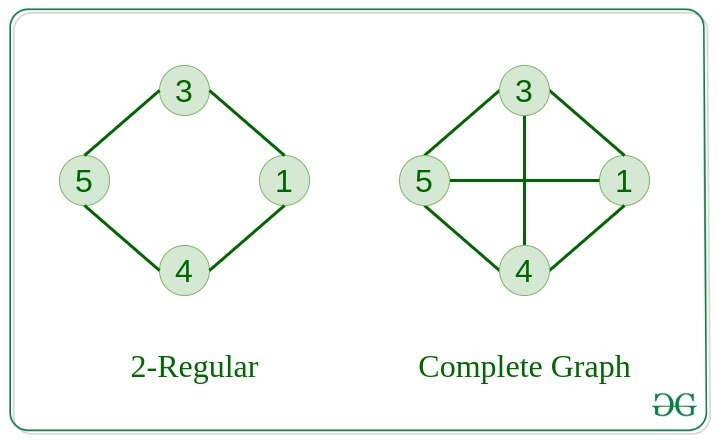
-
Cycle Graph
그래프 전체가 순환될 수 있을 때 Cycle Graph라고 말합니다. -
Cyclic Graph
그래프의 일부분이 순환될 수 있을 때 Cycli Graph라고 말합니다.
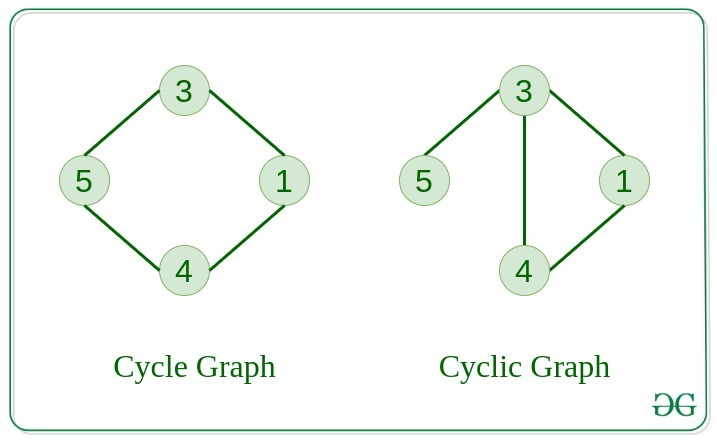
-
Directed Acyclic Graph
방향 그래프 중에서 Cyclic이 존재 하지 않는 그래프입니다. -
Bipartite Graph
노드가 두개의 집합으로 나눠질 수 있는 그래프로 같은 집하에 있는 노드끼리는 간선을 가지지 않습니다.
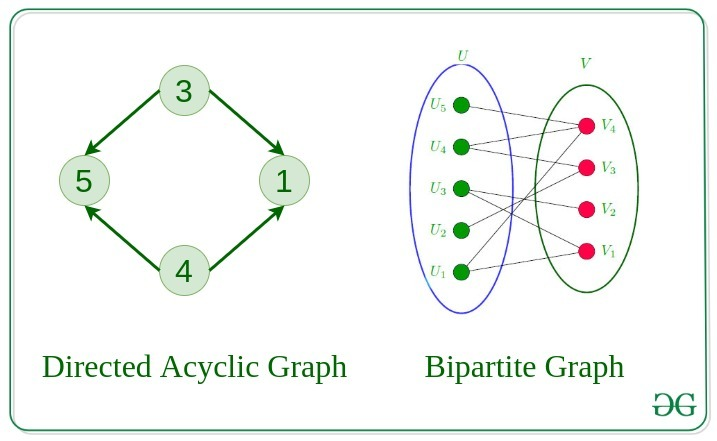
-
Weighted Graph
그래프의 간선에 가중치를 가지고 있는 그래프를 Weighted Graph라고 합니다.
Weighted Graph는 방향성을 가지고 있냐 없냐에 따라
Directed Weighted Graph와 Undirected Weighted Graph로 나뉩니다.
Graph를 표현하는 방법
그래프를 표현하는 방법은 크게 두 가지가 있습니다.
1. 인접 행렬
인접 행렬은 2차원 매트릭스를 이용해 그래프를 표현하는 방식입니다.
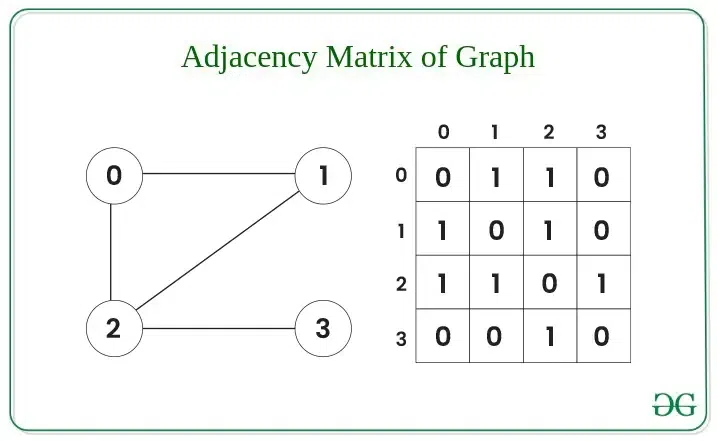
- 인접 리스트
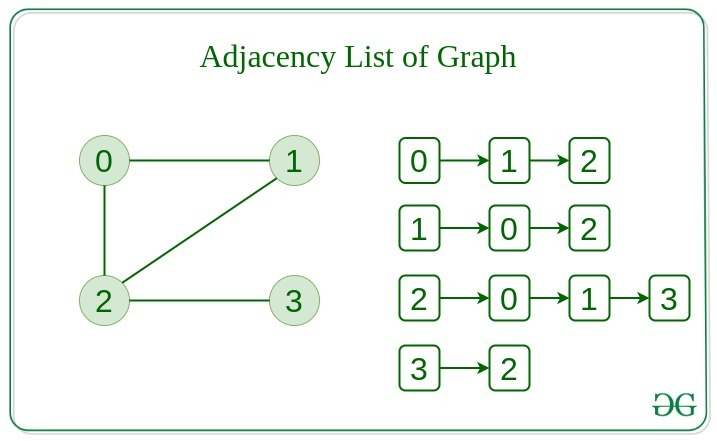
인접 리스트는 각 노드가 간선으로 이어져있는 노드들을 리스트를 통해 표현함으로써 그래프를 표현합니다.
아래는 연결 리스트를 통해 그래프를 표현한 예시입니다.
Graph의 연산
- Insertion or Deletion of Nodes in the Graph
- Insertion or Deletion of Edges in the Graph
- Searching
- Traversal
Tree VS Graph
트리는 그래프의특수한 형태입니다.
모든 트리는 그래프이지만 모든 그래프가 트리인 것은 아닙니다.
Graph의 이점
- 관계를 표현할 수 있는 자료구조
- 경로 찾기나 데이터 클러스터링, 네트워크 분석, 머신러닝과 같은 많은 분야의 문제를 해결하는데 사용된다.
- 복잡한 문제를 푸는데 매우 효율적인 자료구조
- 복잡한 자료구조를 쉽게 표현해서 이해하기 쉽게 만들어 줌
Graph의 단점
- 그래프는 복잡하며 이해하기 힘듦 (그래프 이론과 관계 알고리즘에 대한 이해를 필요로 함)
- 그래프를 만들거나 조작하는 것은 많은 비용을 요구
- 그래프와 관련된 알고리즘은 디자인 하기 어렵고 적절히 구현하기 힘듦
- 그래프 자료 구조는 시각화하기 어렵고 분석하기 어려움
- 그래프 자료 구조에서 의미 있는 데이터를 통한 통찰력 획득도 어려움