Heap

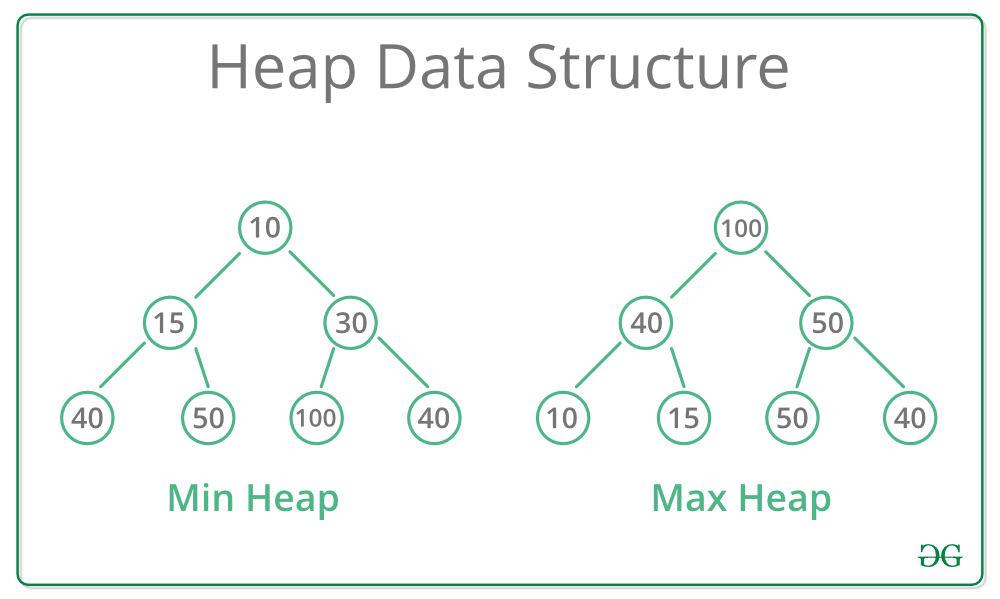
힙은 완전이진트리구조를 지닌 특별한 형태의 트리입니다.
힙의 모든 노드는 자신의 부모 노드보다 크거나 작은 값을 가집니다.
힙은 주로 우선순위 큐를 구현하기 위해 사용됩니다.

Heap의 유형

힙은 일반적으로 2가지 형태를 가집니다.

1. Max-Heap
   Max-Heap에서는 루트 노드가 가장 큰 값을 지니고 모든 노드는 무조건 자식 노드보다 큰 값을 가집니다.

2. Min-Heap
   Min-Heap에서는 루트 노드가 가장 작은 값을 지니고 모든 노드는 무조건 부모 노드보다 큰 값을 가집니다.

Heap의 특성

• 완전 이진 트리
• 루트 노드는 무조건 모든 노드 값 중에 가장 작거나 크다
• Heap에 있는 부모 노드와 자식 노드의 관계는 부모 노드 N일때 자식 노드 2N, 2N+1 위치에 있다
• 효율적인 삽입과 삭제
• 극값에 대한 효율적인 접근

Heap의 Operations

참고할 사항이 있습니다. Max-Heap과 Min-Heap은 Operations에 있어서 원리는 완전히 똑같습니다.

1. Heapify
   Heapify는 요소들을 재배치하여 힙 구조에 맞는 순서를 가지게 하는 것입니다.
   이는 힙에 노드가 만들어졌을 때 힙의 특성을 만족하지 못한다면 실행되는 연산입니다.

2. Insertion
   힙에 값을 삽입합니다.
   만약 여기서 값의 삽입이 힙의 특성을 지키지 못한다면 Heapify를 합니다.

3. Deletion
   힙에서는 언제나 요소의 삭제가 루트 노드에서 일어납니다.
   루트 노드에서 삭제가 일어나면 힙의 특성이 깨지기 때문에 Heapify를 합니다.

4. getMax Or getMin
   Max-Heamp에서 가장 큰 값을 가져오거나 Min-Heap에서 가장 작은 값을 가져옵니다.

5. removeMin Or removeMax
   Max-Heap에서 가장 큰 값을 삭제하거나 Min-Heap에서 가장 작은 값을 삭제합니다.

Heap의 이점

• 극대/극솟값에 대한 빠른 접근(O(1))
• 효율적인 삽입과 삭제 연산 (O(log n))
• 배열을 통한 쉬운 구현
• 실시간 애플리케이션에 적합

Heap의 단점

• 극대/극솟값이 아닌 값을 찾는다면 매우 비효율적
• 힙을 유지하기 위한 추가적인 메모리 오버헤드 필요
• 우선순위가 없는 큐에 쓰기에는 너무 느림