Division
나눗셈은 빼기와 쉬프트로 구현이 가능하다.
곱셈에 쓰였던 하드웨어가 그대로 나눗셈에 사용될 수 있다.
Dvidend = Quotient*Divisor+Reminder
division of unsigned binary integers
Signed Division
곱하기보다는 더 복잡하다.
부호가 없는 나눗셈 알고리즘이 부호가 있는 나눗셈 알고리즘으로 확장 가능하다.
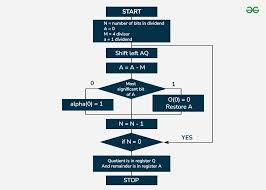
1. 초기화
나누는 수(Divisor)를 M에 로드한다.
나눠지는 수(Dividend)를 A와 Q에 로드한다.
Q: 몫(Quotient)을 저장하는 레지스터
A: 나눗셈 과정에서 보조 역할을 하는 레지스터
2. 반복 연산 (n 비트 동안 반복)
(1) A와 Q를 왼쪽으로 1비트 시프트(shift left)
A와 Q를 한 덩어리로 취급하여 1비트씩 왼쪽으로 이동
이 과정에서 Q의 최상위 비트가 A로 이동
(2) A와 M의 부호 비교
A와 M의 부호가 같으면 A = A - M
A와 M의 부호가 다르면 A = A + M
(3) A의 상태에 따라 Q 업데이트
A의 부호가 변하지 않았거나 A가 0이라면, Q의 최하위 비트에 1 저장
A의 부호가 변했다면, Q의 최하위 비트에 0 저장
(4) A의 부호가 변했다면 원래대로 복원
A와 M을 뺀 후 부호가 변했다면, 다시 A = A + M (복원 과정)
3. 결과 확인
Q 레지스터에 몫(Quotient)이 저장됨
A 레지스터에 나머지(Remainder)가 저장됨
정리된 알고리즘 (n비트 실행)
A, Q, M을 초기화
(n회 반복)
A와 Q를 왼쪽 시프트
A와 M을 비교하여 A - M 또는 A + M 수행
A의 상태를 확인하여 Q의 최하위 비트를 업데이트
필요하면 A를 복원
나눗셈 종료 후 Q가 몫, A가 나머지
덧셈, 뺄셈, 곱셈, 나눗셈 모두 하나의 Adder로 만들 수 있다. 이게 중요하다.
곱셈, 나눗셈 같은 경우 성능이 더 좋은 방법을 사용하긴 한다.
자세하게 배우지는 못한다.
Real Numbers
지금까지 본 것은 정수에 대한 내용이였다.
이제는 실수까지 생각해보자.
실수 연산기는 정수 연산기보다 크다. 회로가 크다.
실수는 소수부가 존재하는 수이다.
binary로 실수를 표현할 수 있다.
binary에서 어떻게 소수점을 표현할 것인가?
1. Fixed Point
정수부와 소수부의 구역을 미리 정해둔다.
이 방법은 간단하지만 최댓값 표현과 최솟값 표현에 큰 제한이 생긴다.
2. Floating Point
.의 위치를 고정해두지 않는 방법이다.
예시 976,000,000.000 = 9.76 10^14
더 정확하게는 아래와 같다.
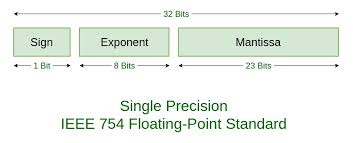
ex) 1.1010001 2^10100 = 0 10010011 10100010000000000000000
Base는 표현하지 않는데 Base는 2로 고정하기 때문이다.
Exponent는 2의 보수로 표현한다. 양수, 음수 표현이 가능하고 충분히 큰 제곱을 표현할 수 있기 때문이다.
한 가지 유의할 점은 -128~127 범위가 아니라 -127~128 범위를 가진다.
이는 큰 수를 표현하는 것이 더 중요하기 때문이다.
위 범위를 가지기 위해 Exponent는 01111111이 0이다. 즉 127을 0으로 기준을 재정의한다.
또한 Floating은 정수부 소수부를 따로 비교하는 것이 아니라 하나의 Integer로 취급해서 비교한다.
지수가 크면 무조건 값이 크기 때문이다.
Significand
무조건 a.????????????? 형태로 변환된다.
추가로 위와 같이 될 경우 0이 표현이 안되는데 그렇기 때문에 모든 비트가 0이면 0으로 취급한다.
예제
- 0 = 0 00000000 00000000000000000000000
- 0.5 = 0 0000.1000 = 0 01111110 000000000000000000000000
- 1.25 = 0 0001.0100 = 0 01111111 0100000000000000000000000
- 0.127 = 0 0000.0001000000001... 0 00000000 00000000100000000000000
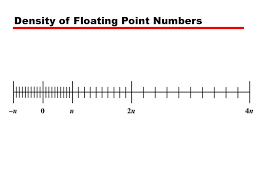
Density of FP Numbers
부동소수점 표현 방식에서는 숫자의 분포가 균등하지 않다.
0 주변에서는 촘촘하지만 멀어질 수록 느슨해진나.
NaN
연산이 불가능하거나 숫자가 아닌 값이 나올때 사용되는 연산자.