[Algorithm] BFS(Tree, Gragh)

BFS(Breadth-First Search)는 너비를 우선으로 탐색하는 알고리즘이다.

재귀를 활용하는 DFS(Depth-First Search, 깊이 우선 탐색)와는 다른 알고리즘으로 접근해야했고, 이머시브 코스 중 토이(오전 1시간 알고리즘 풀기)에서 마주쳤을 때 1시간 안에 풀지 못해서 블로깅하며 다시 공부한다.

Tree의 BFS와 Gragh의 BFS 두 가지를 알아본다.

Tree BFS

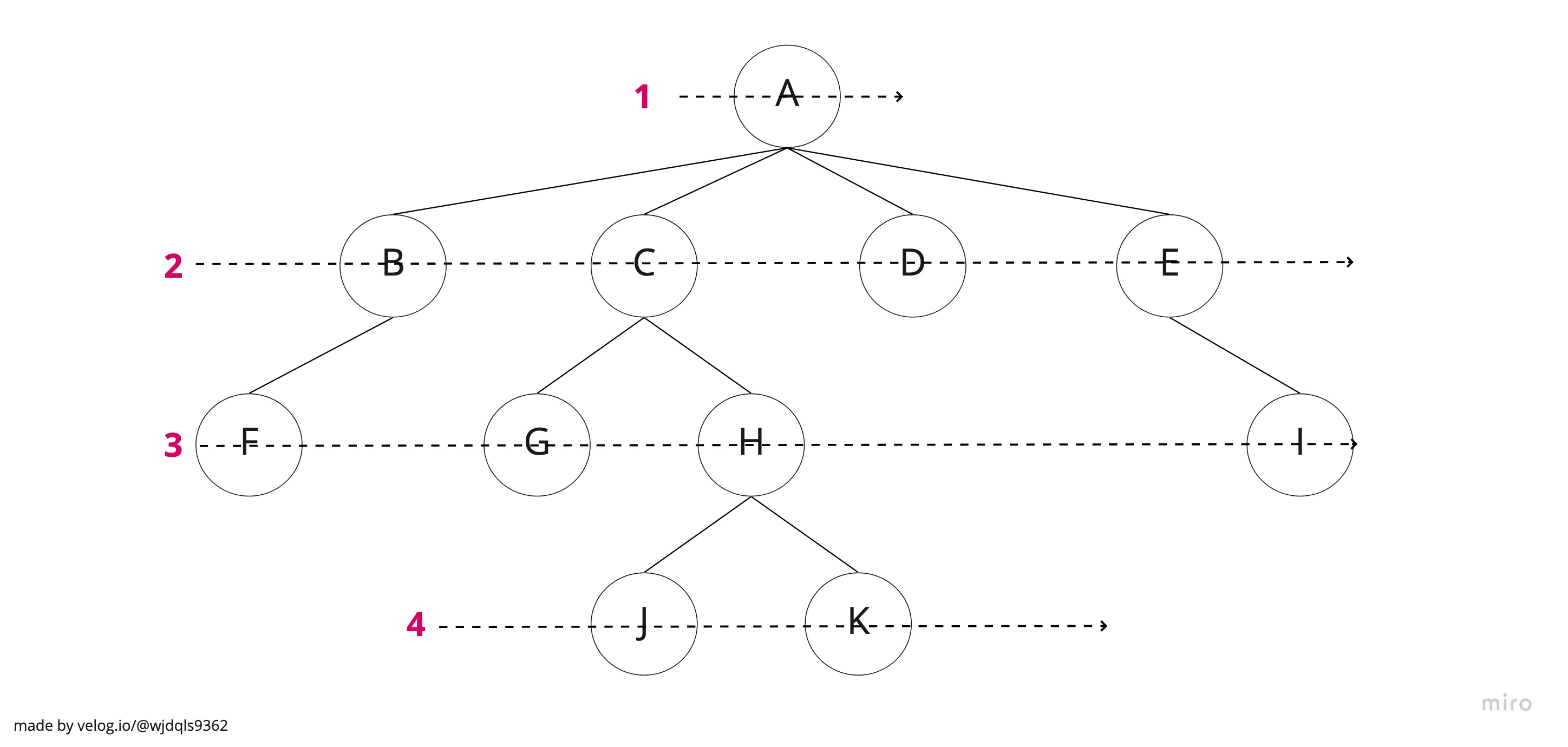
Tree의 BFS는 그림처럼 깊이를 하나의 층으로 생각하고 층별로 훑어내려간다.
(탐색 순서 : A > B > C > D > E > F > G > H > I > J > K)
이는 First in First out 구조를 가진 자료구조 Queue(큐)를 이용해 구현한다.
가장 최상단 노드를 삽입한 후에 그의 자식이 있다면 뒤로 계속 추가하고, 탐색한 노드는 삭제를 하는 로직을 이용한다. 순차적으로 뒤에 자식노드들이 쌓이기 때문에 층별로 탐색하게 된다. 큐 안의 모든 노드가 삭제되면 로직이 끝나게 될 것이다.

function treeBFS(node) { // 최상단 노드를 인자로 받음
  let queue = [node]; // queue 생성
  const values = []; // 검색 값을 저장하는 배열
  while (queue에 노드가 담겨 있을 때까지) {
    // 1. queue의 첫 노드의 값을 values에 저장
    // 2. 첫 노드의 자식(children : 배열로 존재)을 순회하며 queue에 순차적으로 저장
    // 3. 첫 노드 삭제
  }
  return values;
}

Gragh BFS

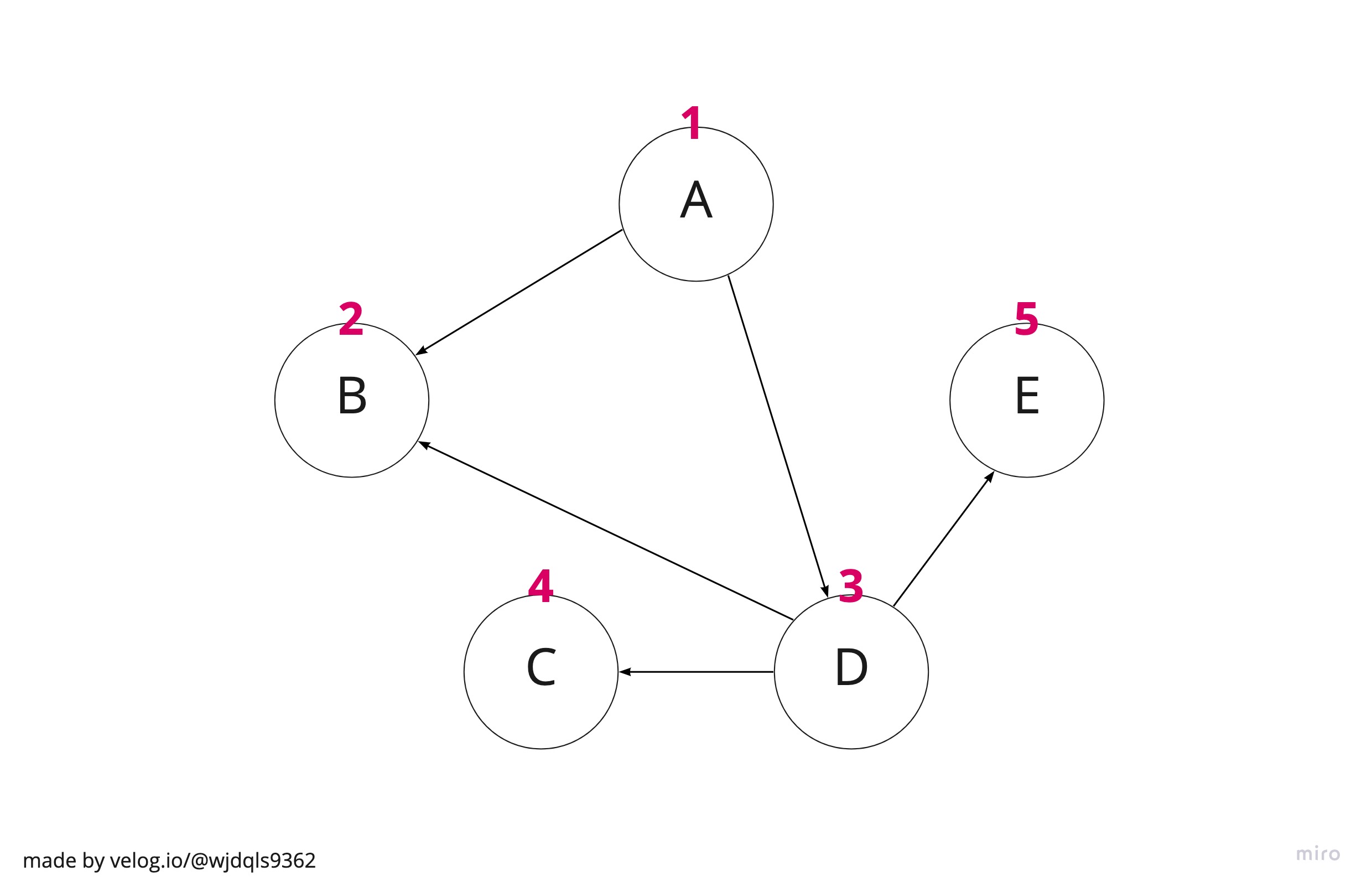
Gragh의 BFS도 동일하게 큐를 이용하지만 층의 개념이 존재하지 않기 때문에, 층 개념을 제외하고 시작 노드의 인접(연결) 노드를 기준으로 큐에 저장하면서 탐색한다.
(탐색 순서 : A > B(A인접) > D(A인접) > C(D인접) > E(D인접))

한 가지 주의할 점은, 한 번 큐에 들어갔던 노드는 다시 큐에 넣지 말아야 한다. 트리와 다르게 부모 자식이 명확하게 구분되어있지 않기 때문이다.

// 그래프는 각 노드의 인접정보가 나타나있는 2차원 배열의 인접리스트로 나타나져 있고, 각 노드의 값은 숫자로 가정

function graghBFS(gragh, start, visited) { // 그래프, 시작노드의 값, 현재 그래프의 노드개수 길이의 방문기록(false)을 담은 visitied 배열을 인자로 받음
  let queue = [start];
  visited[start] = true; // 시작노드는 true로 방문 처리
  const values = [];
  while (queue에 노드가 담겨있을 때까지) {
    // 1. start를 values에 저장 후 큐에서 삭제
    // 2. 그래프 start노드의 인접정보 중 visited에서 방문기록이 false인 값을 순서대로 큐에 삽입
    // 3. 큐에 삽입된 인접 노드들은 visited에서 true 처리
  }
  return values;
}