[ADsP] 3과목 정리(3)

전민정·2025년 5월 6일

ADsP

ADsP 자격증

목록 보기

3/15

4장 통계 분석

1절 통계분석의 이해

(1) 통계 및 자료 획득 방법

통계 정의

특정 집단을 대상으로 수행한 조사나 실험을 통해 나온 결과에 대한 요약된 형태의 표현 - 표, 그림, 그래프
ex) 일기예보, 물가/실업률/GNP, 정당 지지도, 의식조사와 사회조사 분석 통계, 임상실험 등의 실험 결과 분석 통계
필요한 자료 : 조사 또는 실험을 통해 확보, 조사 대상에 따라 전수조사(총조사)(census)와 표본조사로 구분

전수 조사

전수 조사(총조사, census)는 특정 집단의 모든 구성원에 대해 데이터를 수집하는 방법이다.
대상 집단 모두를 조사하므로 많은 비용과 시간이 소요되므로 특별한 경우(ex 대규모 연구나 정책 결정 등)를 제외하고는 사용되지 않는다.

표본조사(Sampling)

대부분의 설문조사는 표본조사로 진행되며 모집단에서 샘플을 추출하여 진행하는 조사이다.
모집단(Population) : 조사하고자 하는 대상 집단 전체
원소(Element) : 모집단을 구성하는 개체
표본(Sample) : 조사하기 위해 추출한 모집단의 일부 원소
모수(Parameter) : 표본 관측에 의해 구하고자 하는 모집단에 대한 정보
ex) 모집단 평균, 모집단 편차 등
모집단의 정의, 표본의 크기, 조사방법, 조사기간, 표본추출방법을 정확히 명시해야 한다.

보충학습

통계량(Statistic) : 해당 모집단에서 추출한 표본(sample)을 이용해 만든 것으로 표본들의 함수
ex) 표본 평균, 표본 편차 등
통계적 검정을 위해 특수한 통계량을 사용하기도 하는 것을 검정통계량(test statistic)이라 부르고, 모수를 추정하기 위해 통계량을 구하는 것을 추정량(estimator)라고 부른다.
통계적 추론에서는 표본 통계량으로부터 전체 모집단을 추정
Unbiased estimation $\rightarrow$ 표본이 모집단을 잘 나타나도록 무작위 추출을 해야 함

표본 추출 방법 (중요)

표본조사의 중요한 점은 모집단을 대표할 수 있는 표본 추출이므로 표본 추출 방법에 따라 분석결과의 해석은 큰 차이가 발생한다.(N개의 모집단에서 n개의 표본을 추출할 경우)

단순랜덤추출법(Simple random sampling)

각 샘플에 번호를 부여하여 임의의 n개를 추출하는 방법으로 각 샘플은 선택될 확률이 동일(복원, 비복원 추출)
- 복원: 사과 5개(A, B, C, D, E)가 담긴 상자에서 무작위로 3개를 뽑되, 한 번 뽑은 사과를 다시 상자에 넣고 추첨함
- 비복원 추출: 동일한 사과 5개 중에서 3개를 뽑되, 뽑은 사과는 다시 넣지 않음

계통추출법(Systematic sampling)

단순랜덤추출법의 변형된 방식으로 번호를 부여한 샘플을 나열하여 k개씩 (K=N/n) n개의 구간으로 나누고 첫 구간(1,2,...,K)에서 하나를 임의로 선택한 후 K개씩 띄어서 표본을 선택, 임의 위치에서 매 k번째 항목 추출
- 100명의 명단이 있고, 이 중 10명을 뽑으려 할 때 1부터 10 중 무작위로 시작점(예:4)을 정한 후 매 10번째 항목을 선택 -> 4, 14, 24, ..., 94

집략추출법(Cluster sampling)

군집을 구분하고 군집별로 단순랜덤추출법을 한 후 모든 자료를 활용하거나 샘플링하는 방법(지역표본추출, 다단계표본추출)
- 지역표본추출: 전국을 100개 지역으로 나눈 뒤, 무작위로 10개 지역을 선정하고 해당 지역 주민 전체를 조사
- 다단계표본추출:
  - 1단계: 전국을 100개 시군으로 나눈 뒤 10개 시군을 무작위로 선택
  - 2단계: 각 시군에서 3개 동을 무작위로 선택
  - 3단계: 각 동에서 10명을 무작위로 선택

층화추출법(Stratified random sampling)

이질적인 원소들로 구성된 모집단에서 각 계층을 고루 대표할 수 있도록 표본을 추출하는 방법, 유사한 원소끼리 몇 개의 층(stratum)으로 나누어 각 층에서 랜덤 추출하는 방법(비례층화추출법, 불비례층화추출법)
- 비례층화추출법: 한 학교에 1학년 100명, 2학년 200명, 3학년 300명 있음, 전체 60명을 뽑으려면 1학년:10명(100/600 x 60) 2학년:20명(200/600 x 60) 3학년:30명 (300/600 x 60)
- 불비례층화추출법: 위와 같은 학교에서 각 학년에서 20명씩 균등하게 추출 -> 전체 60명 (각 층의 비율과 무관하게 균등 배분)

**실험 : 특정 목적 하에 실험 대상에게 처리를 가한 후에 그 결과를 관측해 자료를 수집하는 방법(ex. 강의방법의 효과 분석, 암 치료제의 효과 분석)

측정 (척도 중요)

표본조사나 실험을 실시하는 과정에서 추출된 원소들이나 실험 단위로부터 주어진 목적에 적합하도록 관측해 자료를 얻는 것이다.

[측정 방법]
명목척도

측정 대상이 어느 집단에 속하는지 분류할 때 사용(ex. 성별, 출생지 구분)
혈액형(A형, B형, AB형, O형)은 서로 다른 특성을 가지지만, 그 사이에 서열은 없으므로 명목척도이다.

순서척도

측정 대상의 특성이 서열관계를 관측하는 척도(ex. 만족도, 선호도, 학년, 신용등급)
1등급 ~ 9등급은 등급의 숫자가 낮을수록 성적이 높다라는 서열을 가지고 있어 순서척도이다.

명목척도와 순서척도의 차이

서열의 '여부'

질적척도(명목척도, 순서척도)

범주형 자료, 숫자들의 크기 차이가 계산되지 않는 척도

구간척도(등간척도)

측정 대상이 갖고 있는 속성의 양을 측정하는 것으로 구간이나 구간 사이의 간격이 의미가 있는 자료(ex. 온도, 지수)
온도의 경우 0도가 절대적인 '없음'이 아닌 특정한 온도를 의미하므로 구간척도이다.

비율척도

간격(차이)에 대한 배율이 의미를 가지는 자료, 절대적 기준인 0이 존재하고 사칙연산이 가능하며 가장 많은 정보를 가지고 척도(ex. 무게, 나이, 시간, 거리)
길이의 경우 0cm는 '길이가 없음'을 의미하므로 비율척도이다.

구간척도와 비율척도의 차이

'절대적 영점'의 존재

양적척도(구간척도, 비율척도)

수치형 자료, 숫자들의 크기 차이를 계산할 수 있는 척도

(2) 통계 분석 (중요)

정의

특정한 집단이나 불확실한 현상을 대상으로 자료를 수집해 대상 집단에 대한 정보를 구하고, 적절한 통계분석 방법을 이용해 의사결정을 하는 과정

기술통계(Descriptive statistics)

주어진 자료로부터 어떠한 판단이나 예측과 같은 주관이 섞일 수 있는 과정을 배제하여 통계집단들의 여러 특성을 수량화하여 객관적인 데이터로 나타내는 통계분석 방법론(ex : 평균, 표준편차, 중위수, 최빈값, 그래프 등 활용)

추론통계(Inference statistics)

수집된 자료를 이용해 대상 집단(모집단)에 대한 의사결정을 하는 것
모수 추정 : 표본집단으로부터 모집단의 특성인 모수 (평균, 분산 등)를 분석하여 모집단을 추론
가설 검정(Hypothesis test) : 대상 집단에 대해 특정한 가설을 설정한 후에 그 가설의 채택 여부를 결정하는 방법론
예측(Forecasting) : 미래의 불확실성을 해결해 효율적인 의사결정을 하기 위해 수행

(3) 확률과 확률 분포

확률 (중요)

확률 : 특정 사건이 일어날 가능성의 척도
표본 공간(Sample space, Ω) : 어떤 실험을 실시할 때 나타날 수 있는 모든 결과들의 집합
원소(Element) : 나타날 수 있는 개개의 결과들
사건(Event) : 관찰자가 관심이 있는 사건으로 표본공간의 부분집합
표본공간 Ω의 부분집한인 사건 E의 확률은 P(E)는 표본공간의 원소의 개수에 대한 사건 E의 개수의 비율로 다음과 같이 정의함
- ex) 10개 공 중에 빨간 공이 4개고 빨간 공을 뽑을 확률 4/10 = 0.4 $P(E) = \frac{n(E)}{n(\Omega)}$

확률 변수(Random Variable) (중요)

특정 값이 나타날 가능성이 확률적으로 주어지는 변수
정의역(Domain)이 표본공간, 치역(Range)이 실숫값인 함수 0이 아닌 확률을 갖는 실수값의 형태에 따라 이산형 확률변수(Discrete random variable)와 연속형 확률변수(Continuous random variable)로 구분된다.

보충학습

이산 확률 변수(Discrete random variable)

표본 공간(X)이 유한하거나 가산적인 무한이라면 X는 이산 확률 변수
X가 값 x를 갖는 사건의 확률을 확률 질량 함수(PMF, Probability mass function)
확률 질량 함수 공식 $f(x) = P(X = x)$
확률 질량 함수 특징
- 확률은 0과 1 사이이다.
- 표본공간의 합은 1이다.
- 임의의 구간에 있는 확률은 해당되는 구간 안의 모든 것을 더한 것이다.

연속 확률 변수(Continuous random variable)

$X \in R$ 가 실숫값의 양(quantity)이라면, 연속 확률 변수라 부른다.
누적분포함수(CDF, Cumulative Distribution Function)
- 누적분포함수란 확률론에서 주어진 확률분포가 특정 값보다 작거나 같은 확률을 나타내는 함수이다.
- 이 특정 값이라는 것은 어떤 사건을 의미하므로 누적분포함수는 어떤 사건이 얼마나 많이/적게 나타나는지에 관한 함수라고 할 수 있다.
- 누적분포함수의 대표적인 특징
  - 확률변수가 이산형/연속형과 무관하게 모든 실수값을 출력한다.
- 누적분포함수 공식
  
  $F(a) = P(X \leq a) = \sum_{x \leq a}P(x)$
확률밀도함수(PDF, Probability Density Function)
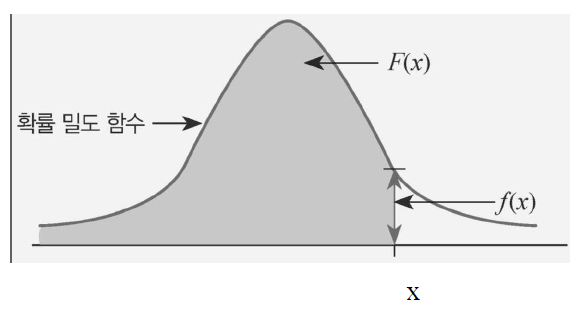
- 확률밀도함수는 연속 사건에서 x가 주어졌을 때의 확률을 구하는 함수이다.
- 확률밀도함수 f(x)와 구간[a,b]에 대해서 확률 변수 X가 구간에 포함될 확률
- 확률밀도함수 공식
  
  $P(a \leq X \leq b) = \int_a^b\;f(x)\mathrm{d}x$
- 확룔밀도함수는 두 조건을 만족해야 한다
  - 모든 실수 값 $x$ 에 대해 $f(x) \geq 0$
  - $\int_{-\infty}^{\infty}\;f(x)dx = 1$
확률밀도함수와 누적분포함수는 다음과 같은 수식이 성립함
$F(x) \int_{-\infty}^{\infty}$
$f(x) = \frac{d}{dx}F(x)$
- 누적밀도함수를 미분하여 나온 도함수(derivative)를 확률밀도함수라고 함

간단 용어 정리
표본공간: 사건에서 발생 가능한 모든 결과의 집합
확률변수: 표본공간에서 일정 확률을 갖고 발생하는 사건에 수치를 일대일 대응시키는 함수
확률분포: 흩어진 확률변수를 모아 함수 형태로 만든 것
이산확률변수: 확률변수 개수가 유한해 정수 구간으로 표현되는 확률변수
연속확률변수: 확률변수 개수가 무한해 실수 구간으로 표현되는 확률변수
확률질량함수 : 이산확률변수 X의 분포를 나타내는 함수로, 함수 값이 곧 확률이다.
확률밀도함수 : 연속확률변수 X의 분포를 나타내는 함수로, 함수의 넓이가 확률이다

[확률/통계] 누적분포함수 (CDF, Cumulative Distribution Function)
확률 밀도 함수 PDF (Probability Density Function)
참고[확률분포함수와 확률밀도함수의 의미]

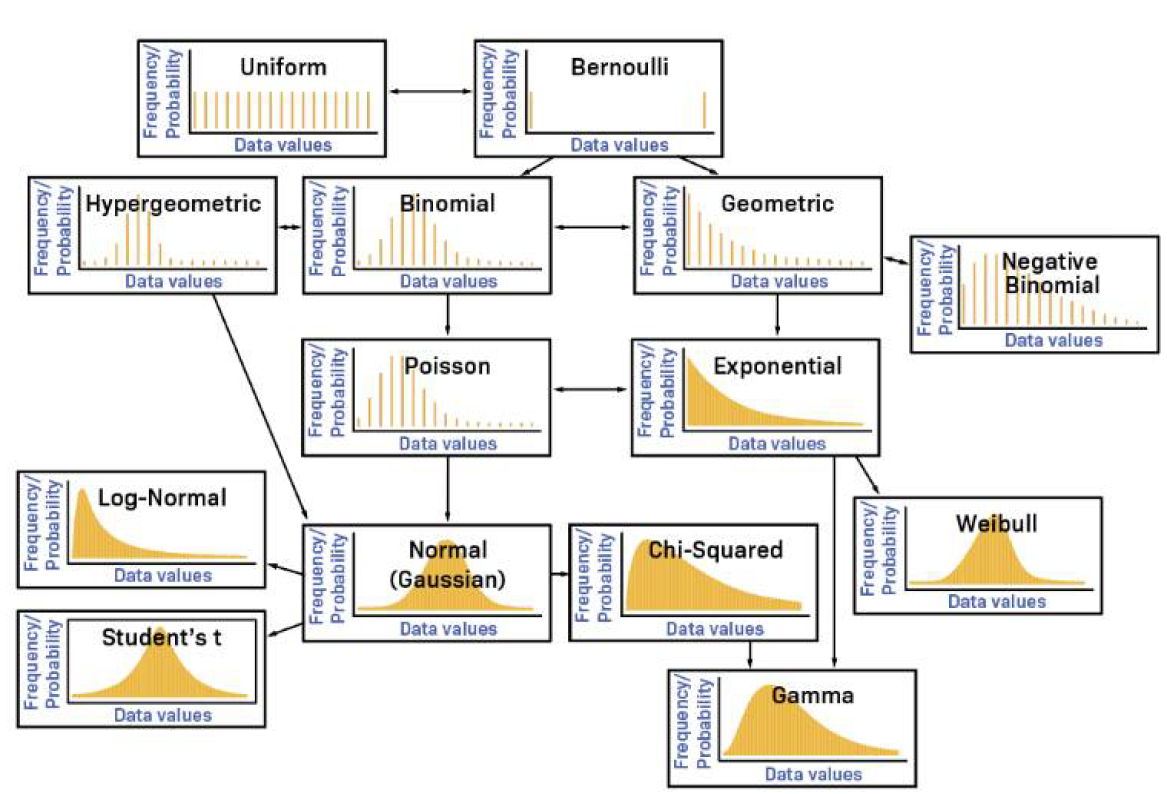
이산형 확률분포 : 0이 아닌 확률값을 갖는, 실숫값이 셀 수 있는 경우 (확률질량함수)
- ex) 주사위(1~6)를 던졌을 때, 1이 나올 확률

p_i = P(X = x_i), i = 1, 2, \dots, n

베르누이 확률분포(Bernoulli distribution) : 결과가 2개만 나오는 경우
- ex) 동전 던지기, 시험의 합격/불합격 등

P(X = x) = p^x \cdot (1 - p)^{1 - x}, \quad (x = 1 \text{ or } 0), \quad E(X) = p, \quad \text{var}(X) = p(1 - p)

이항분포(Binomail distribution) : 베르누이 시행을 n번 반복했을 때 k번 성공할 확률
- p가 0이거나 1에 가깝지 않고 n이 충분히 크면 이항분포는 정규분포에 가까워짐, p = 1/2에 가까우면 종 모양이 됨

P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k}, \quad \binom{n}{k} = \frac{n!}{k!(n - k)!}, \quad X \sim B(n, p), \quad E(X) = np, \quad \text{var}(X) = np(1 - p)

기하분포(Geometric distribution) : 성공 확률이 p인 베르누이 시행에서 첫 번째 성공이 있기까지 x번 실패할 확률
- ex) 야구선수가 5번째 타석에서 홈런 칠 확률
다항분포(Multinomial distribution) : 이항분포의 확장한 것으로 세 가지 이상의 결과를 가지는 반복 시행에서 발생하는 확률 분포
포아송(Poisson distribution) : 시간과 공간 내에서 발생하는 사건의 발생 횟수에 대한 확률 분포
- ex) 책에 오타가 5페이지에 10개씩 나온다고 할 때, 한 페이지에 오타가 3개 나올 확률

연속형 확률분포 : 가능한 값이 실수의 어느 특정 구간 전체에 해당되는 확률(확률밀도함수)
- 연속형 확률분포 대표적인 분포는 정규분포
- 지수분포, 와이블 분포, 카이제곱분포, t분포, f분포 등 $f(x) \geq 0, \quad \int f(x) \, dx = 1$
균일분포(일양분포, Uniform distribution) : 모든 확률변수 X가 균일한 확률을 가지는 확률분포
- ex) 다트의 확률분포

E(x) = (a + b)/2 \quad \text{var}(x) = (b - a)^2/12

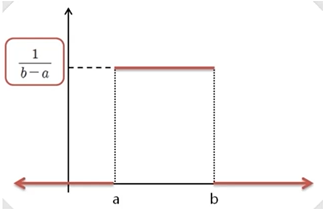
특정 구간인 a에서부터 b까지의 일어날 확률이 일정함
a와 b를 벗어날 경우 확률이 0
a구간과 b구간에서 나올 수 있는 확률값은 확률밀도함수 밑에 나오는 면적들을 다 더하면 확률이 1(100%)이 나온다.
확률이 100%가 나오려면 확률값은 1/(b-a)을 되어야 곱했을 때 1이 됨
확률변수의 기댓값은 50%가 되는 부분이고, 그 값은 (a+b)/2이다.
$(b-a) * \frac{1}{(b - a)} = 1$
정규분포(Normal distribution) : 평균이 μ이고, 표준편차가 σ인 x의 확률밀도함수

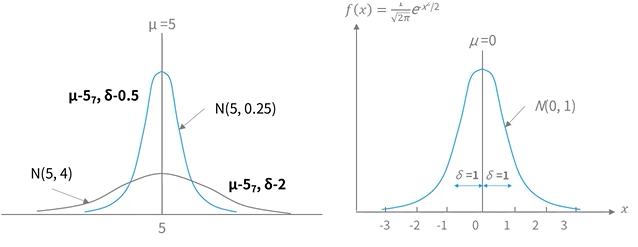
f_X(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x - \mu)^2} {2\sigma^2}} \quad - \infty < x < \infty

평균이 5이고, 표준편차가 0.25인 경우 평균을 중심으로 밀집되어 있는 형태로 분포(뾰쪽한)
표준편차가 4이면 퍼져있는 종모양 형태
정규분포 특징
- 평균을 중심으로 대칭
- 평균, 표준편차에 따라 종 모양이 결정
- 평균, 중앙값, 최빈값이 동일하다.
- 정규분포는 분포 선 밑에 있는 부분을 다 더하면 1(100%)이다.
- 양쪽 끝이 붙지 않고 쭉 간다. 그래서 -무한대에서 무한대까지 x값이 존재한다.
두 정규분포 비교를 위해 표준화할 수 있는데, 표준화한 분포를 '표준정규분포'하고 한다.
표준정규분포는 평균이 0이고 표준편차가 1인 정규분포를 말한다.
표준정규분포를 만들기 위해 Z라는 값으로 값을 치환해서 활용함
$Z = \frac{x - \mu}{(\sigma)}$
이 공식을 활용해서 표준화시킨 Z의 확률분포가 표준정규분포의 확률분포가 된다.
정규분포를 활용해서 확률값들을 계산하는 방법
- x라는 분포가 정규분포라고 할 때, 평균값과 표준편차를 Z값으로 치환하게 되고 분포는 평균이 0이고 표준편차가 1인 형태인 분포가 만들어진다. $X \sim N(\mu, \sigma^2)일\quad때, \quad Z = \frac{x - \mu}{(\sigma)} \sim N(0,1)$
정규분포의 확률밀도함수
- Z=0일 때 확률 밀도 함수의 값은 대략 0.3989
- 확률밀도값이 거의 0에 해당
- 표준정규분포의 확률밀도함수는 0.4보다 작은 값으로 구성된다는 특징이 있다.
  $f(z) = \frac{1}{\sqrt{2\pi}} e^{-{z^2}/2} \quad - \infty < x < \infty$
- 표준정규분포 값이 1일 때, 표준정규분포의 z값은 얼마일까?
  $f(1) = \frac{1}{\sqrt{2\pi}} e^{-{1^2}/2} = \frac{1}{\sqrt{2\pi}} e^{-{1}/2} \quad f(1) \approx \frac{0.6065}{2.5066} \approx 0.24197$
표준 정규 분포표(Standard Normal Distribution Table)는 P(Z>a), P(Z<b), P(a<Z<b)와 같은 확률을 편하게 계산하기 위해 확률을 정리해 놓은 표

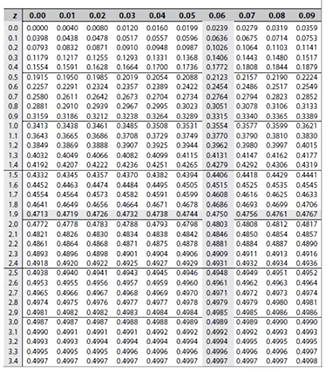
$즉, F(z)= \int f(x)dx를\quad계산하는\quad것이\quad어렵기\quad때문에 \quad f(z)값들을\quad정리해\quad놓은\quad것$

- 표준 정규 분포표는 누적분포함수(누적확률밀도함수)로 만들어졌디.
- Z값이 0일 경우 0.5에 해당하는 확률값을 가지게 된다.
- ex) Z값이 1이면 0.3413, 값이 1 이하일 확률이면 0.5 + 값을 더해주면 0.8413이 된다.
- ex2) 90%에 해당하는 면적은 0.5 + 0.4가 되는데, 이 때 확률이 0.4를 보면 된다. 확률이 0.4가 되는, 1.285가 된다.
- (Z값이 0.5 기준일 때)'~ 이하일 확률'을 구하는 경우 (ex) P[Z<=0.61] = 0.7291
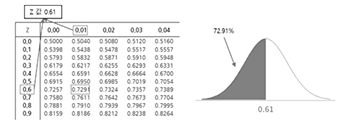
  - (Z값이 0 기준일 때) 0.61에 해당하는 값이 0.2291, 0.2291에 0.5를 더하면 0.7291이 된다.
- (Z값이 0 기준일 때)'~ 이상일 확률'을 구하는 경우 (ex) P[Z<=0.75] = 1 - 0.7734 = 0.2266
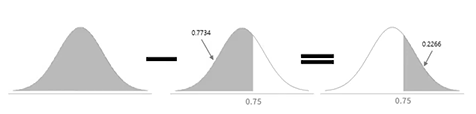
  - 이상일 확률을 구할 경우 전체 1에서 이하일 확률을 빼면 이상일 확률이 나온다.
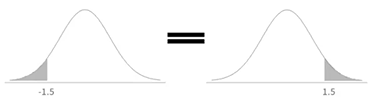
- 'Z값이 음수일 때 확률'을 구하는 경우(대칭이라는 특성을 활용)
  ex) P[Z<=-1.5] = P[Z>=1.5] = 1 - 0.9332 = 0.0668
- 일정구간의 확률을 구하는 경우
  ex) P[-1.21<=Z<=1.57] = P[Z<=1.57] - P[Z>=1.21] = 0.9418 - 0.1131 = 0.8287

(예제) 어느 회사에서 직원들의 근무 기간을 조사하였다. 직원들의 근무기간은 평균이 11년이고 분산이 16년인 정규분포를 따른다고 한다. 이 회사에서 14년 이상 근무한 직원의 비율을 구하시오.

(Solution) 평균이 11이고 분산이 16인 정규분포를 표준정규분포로 변환한다.

P(X\geq14) = P(Z\geq\frac{14-11}{4}) = P(Z\geq0.75)

Z값이 0.75이며 표준정규분포표에서 0.75에 해당하는 값을 찾으면 0.7734이다. "이상일 확률"을 구하는 것이므로 1 - 0.7734를 계산하면 14년 이상 근무한 직원의 비율은 22.66%이다.

지수분포(Exponential distribution)

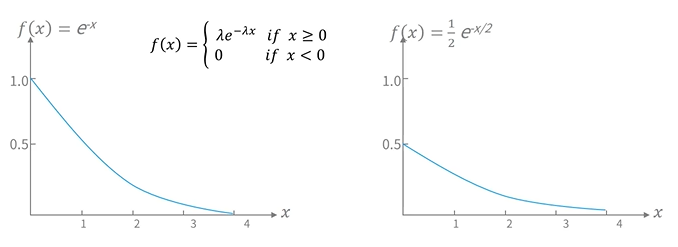
- 분포 형태가 단조감소하는 형태를 가지는 분포
- 모수가 평균과 표준편차가 아니고 람다이다.
- 0 이상의 값들만 존재, 0 이하의 값들은 존재하지 않는다.
t-분포(t-distribution)
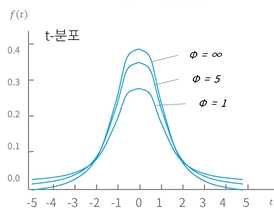
- 두 집단의 평균이 동일한지 알고자 할 때 활용하는 검정통계량
- 정규분포보다 더 퍼져있는 형태
- 자유도가 증가할수록 정규분포 형태를 띈다.
- 모집단의 분산을 모를 경우, 모집단의 개체 수가 작을 경우 사용한다.
x^2분포(chi-square distribution)

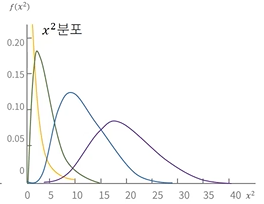
- 모평균과 모분산이 알려지지 않은 모집단의 모분산에 대한 가설 검정에 사용되는 분포
- 두 집단간의 동질성 검정에 활용됨
- 범주형 자료에 대해 얻어진 관측값과 기댓값의 차이를 보는 적합성 검정에 활용
- 한쪽으로 치우쳐져 있고, 자유도가 점점 증가할수록 정규분포 형태를 띈다.
F-분포(F-distribution)

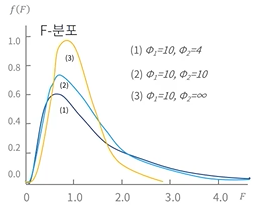
- 두 집단간 분산의 동일성 검정에 사용되는 검정 통계량의 분포
- 우쪽으로 꼬리가 긴 형태에서 자유도가 증가할수록 점점 짧아진다.
- 2가지 자유도를 활용해서 f-분포를 만드는데, 2가지를 같이 비교할 때 f-분포를 사용한다.