[자료구조] Java - Set

Set

• Set 은 중복을 허용하지 않고, 순서를 보장하지 않는 자료구조이다.
• Set 은 수학적 집합 개념을 구현한 것으로, 특정 요소가 집합에 있는지 여부를 확인하는데 최적화되어 있다.

상속 구조

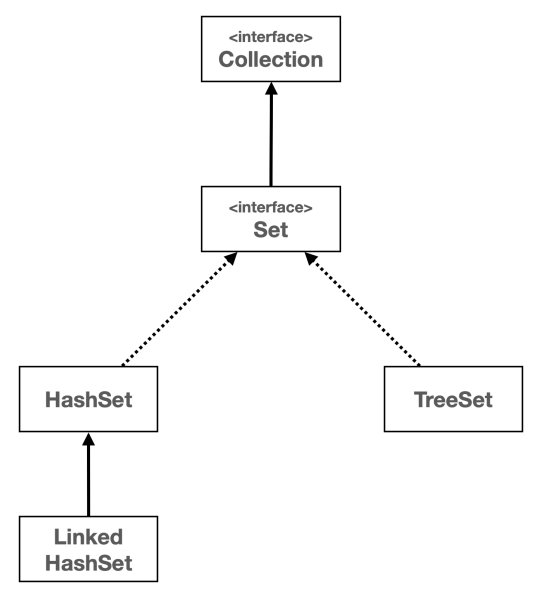
출처: 김영한님의 자바 강의 PDF

자바의 Set 인터페이스는 HashSet, LinkedHashSet, TreeSet 등의 여러 구현 클래스를 가지고 있으며, 각 클래스는 Set 인터페이스를 구현하며 각각의 특성을 가지고 있다.

Set 인터페이스의 주요 메서드

메서드	설명
add(E e)	지정된 요소를 Set에 추가한다(이미 존재하는 경우 추가하지 않음)
addAll(Collection<? extends E> c)	지정된 컬렉션의 모든 요소를 Set에 추가한다.
contains(Object o)	Set이 지정된 요소를 포함하고 있는지의 여부를 반환한다.
containsAll(Collection<?> c)	Set이 지정된 컬렉션의 모든 요소를 포함하고 있는지의 여부를 반환한다.
remove(Object o)	지정된 요소를 Set에서 제거한다.
removeAll(Collection<?> c)	지정된 컬렉션에 포함된 요소를 Set에서 모두 제거한다.
retainAll(Collection<?> c)	지정된 컬렉션에 포함된 요소만을 유지하고 나머지 요소는 Set에서 제거한다.
clear()	Set에서 모든 요소를 제거한다.
size()	Set에 있는 요소의 수를 반환한다.
isEmpty()	Set이 비어있는지의 여부를 반환한다.
iterator()	Set의 요소에 대한 반복자를 반환한다.
toArray()	Set의 모든 요소를 배열로 반환한다.
toArray(T[] a)	Set의 모든 요소를 지정된 배열로 반환한다.

---

HashSet 특성

• 구현: 해시 자료 구조를 사용해서 요소를 저장한다.
• 순서: 요소들은 특정한 순서 없이 저장된다. 즉, 요소를 추가한 순서를 보장하지 않는다.
• 시간 복잡도: HashSet의 주요 연산(추가, 삭제, 검색)은 평균적으로 O(1)의 시간 복잡도를 가진다.
• 용도: 데이터의 유일성만 중요하고, 순서가 중요하지 않은 경우에 적합하다.

HashSet 의 최적화

• 해시 기반 자료 구조를 사용하는 경우 통계적으로 입력한 데이터의 수가 배열 크기의 75% 정도를 넘어가면 해시 인덱스가 자주 충돌한다.
  • 해시 충돌로 같은 해시 인덱스에 들어간 데이터를 검색하려면 모두 탐색해야 한다. 따라서 성능이 O(n) 으로 좋지 않다.
• 하지만 데이터가 동적으로 계속 추가되기 떄문에 적절한 배열의 크기를 정하는 것은 어렵다.
• 자바의 HashSet은 데이터의 양이 배열 크그의 75%를 넘어가면 배열의 크기를 2배로 늘리고 2배 늘어난 크기를 기준으로 모든 요소에 해시 인덱스를 다시 적용한다.
  • 이 과정을 재해싱(rehashing)이라 한다.
  • 해시 인덱스를 다시 적용하는 시간이 걸리지만, 결과적으로 해시 충돌이 줄어든다.
• 자바 HashSet의 기본 크기는 16이다.

---

LinkedHashSet 특성

• 구현: LinkedHashSet은 HashSet에 연결 리스트를 추가해서 요소들의 순서를 유지한다.
• 순서: 요소들은 추가된 순서대로 유지된다. 즉, 순서대로 조회 시 요소들이 추가된 순서대로 반환된다.
• 시간 복잡도: LinkedHashSet도 HashSet과 마찬가지로 주요 연산에 대해 평균 O(1) 시간 복잡도를 가진다.
• 용도: 데이터의 유일성과 함께 삽입 순서를 유지해야 할 때 적합하다.
• 참고: 연결 링크를 유지해야 하기 때문에 HashSet보다는 조금 더 무겁다.

---

TreeSet 특성

• 구현: TreeSet은 이진 탐색 트리를 개선한 레드-블랙 트리를 내부에서 사용한다.
• 순서: 요소들은 정렬된 순서로 저장된다. 순서의 기준은 비교자(Comparator)로 변경할 수 있다.
• 시간 복잡도: 주요 연산들은 O(log n)의 시간 복잡도를 가진다.
• 용도: 데이터들을 정렬된 순서로 유지하면서 집합의 특성을 유지해야 할 때 사용한다. 범위 검색이나 정렬된 데이터가 필요한 경우에 유용하다. 정렬은 입력된 순서가 아닌 값의 크기 순서이다.

---

간단 사용 예제

import java.util.*;

public static void main(String[] args) {
	run(new HashSet<>());
    run(new LinkedHashSet<>());
    run(new TreeSet<>());
}

private static void run(Set<String> set) {
	System.out.println("set = " + set.getClass());
    set.add("C");
    set.add("B");
    set.add("A");
    set.add("1");
    set.add("2");
    
    Iterator<String> iterator = set.iterator();
    while (iterator.hasNext()) {
    	System.out.print(iterator.next() + " ");
    }
    
    System.out.println();
}

• HashSet, LinkedHashSet, TreeSet 모두 Set 인터페이스를 구현하기 때문에 구현체를 변경하면서 실행이 가능하다.

• iterator()를 호출하면 컬렉션을 반복해서 출력할 수 있다.

  • iterator.hasNext(): 다음 데이터가 있는지 확인한다.
  • iterator.next(): 다음 데이터를 반환한다.

실행 결과

set = class java.util.HashSet
A 1 B 2 C 

set = class java.util.LinkedHashSet
C B A 1 2 

set = class java.util.TreeSet
1 2 A B C