2 x n 타일링 [Programmers]

문제

https://programmers.co.kr/learn/courses/30/lessons/12900#

설명

우선 경우의 수는 다음과 같다.

1=> | [1]
2=> ||, = [2]
3=> |||, |=, =| [3]
4=> ||||, ||=, |=|, =||, == [5]
5=> |||||, |||=, ||=|, |=||, =|||, |==, ==|, =|= [8]
6=> ||||||, ||||=, |||=|, ||=||, |=|||, =||||, ||==, |=|=, |==|, =||=, =|=|, ==||, === [12]

처음에는 규칙을 =가 들어가는 부분이 어떻게 되는지에 대해서 찾았다.
하지만, 뭔가 연관성이 있는 것 같으면서도 규칙을 제대로 발견하기 어려웠다.

그 다음에는 n에 따른 결과에서 규칙을 찾아보았다.

1 => 2 => 3 => 5 => 8 => 12

다르게 생각해보니 규칙을 의외로 쉽게 찾았다.

규칙: n = (n-1) + (n-2)

이제 생각해 볼 것은 재귀 함수와 동적 프로그래밍 중에 풀이 방법을 정하는 것이다.
n의 개수가 최대 60,000까지 주어진 상황에서 재귀 함수는 적절치 않았다.

=> 동적 프로그래밍 선택

동적 프로그래밍으로 선택해 문제를 풀었음에도 자꾸 1,2개씩 시간 초과가 나왔다.

(시간 초과가 뜬 코드)

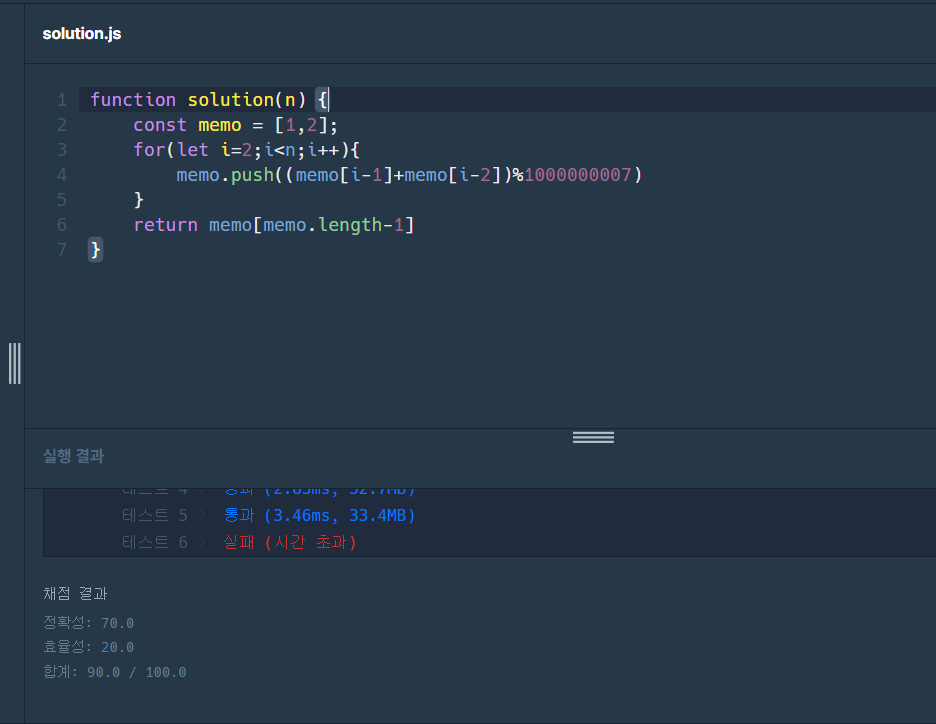
처음에는 새로운 값들을 배열에 하나씩 push하는 방향으로 생각했지만, 배열을 n의 길이로 초기화 시키고, 그 안에 값을 하나씩 넣는 방법이 더 빠르다 생각해서 다음과 같은 코드를 만들었다.

코드

function solution(n) {
    const memo = [1,2,...Array(n-2)]
    for(let i=2;i<n;i++){
        memo[i] = (memo[i-1] + memo[i-2]) % 1000000007
    }
    return memo[n-1]
}