- 서로소의 집합을 판별하고 만들어내는 알고리즘
- 서로 다른 집합을 만들어낸다.
친구인가? 문제
설명
모든 학생은 1부터 N까지 번호가 부여되어 있고, 각각 두 명의 학생은 친구 관계 가 번호로 표현된 숫자쌍이 주어진다. 만약 (1, 2), (2, 3), (3, 4)의 숫자쌍이 주어지면 1번 학 생과 2번 학생이 친구이고, 2번 학생과 3번 학생이 친구, 3번 학생과 4번 학생이 친구이다. 그리고 1번 학생과 4번 학생은 2번과 3번을 통해서 친구관계가 된다.
학생의 친구관계를 나타내는 숫자쌍이 주어지면 특정 두 명이 친구인지를 판별하는 프로그램을 작성하세요. 두 학생이 친구이면 “YES"이고, 아니면 ”NO"를 출력한다.
입력설명
첫 번째 줄에 반 학생수인 자연수 N 숫자쌍의 개수인 M이 주어지고, 다음 M개의 줄에 걸쳐 숫자쌍이 주어진다. 마지막 줄에는 두 학생이 친구인지 확인하는 숫자쌍이 주어진다.
입력예제 1
9 7
1 2
2 3
3 4
1 5
6 7
7 8
8 9
3 8출력예제 1
NO코드
import java.util.*;
public class Main {
static int[] unf;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
unf = new int[n + 1];
for (int i = 1; i <= n; i++)
unf[i] = i;
for (int i = 0; i < m; i++) {
union(sc.nextInt(), sc.nextInt());
}
int a = sc.nextInt();
int b = sc.nextInt();
if (find(a) == find(b))
System.out.println("YES");
else
System.out.println("NO");
}
private static void union(int a, int b) {
int fa = find(a);
int fb = find(b);
if(fa != fb) unf[fa] = fb;
}
private static int find(int v) {
if(v == unf[v]) return v;
else return unf[v] = find(unf[v]);
}
}- unf 배열의 인덱스는 학생번호, 각 값들은 학생이 속한 집합을 의미한다.
처음 UNF배열

- idx - > 학생 번호
- 배열값 → 집합 번호
Union함수
private static void union(int a, int b) {
int fa = find(a);
int fb = find(b);
if(fa != fb) unf[fa] = fb;
}-
find함수를 호출하면 각 학생이 속한 집합의 번호를 리턴한다.
-
a = 1, b = 2일때 unf배열은 다음과 같이 변한다

- 집합의 번호가 다를 시에 unf[fa] = fb; 로 두 학생을 같은 집합으로 처리한다.
find함수
private static int find(int v) {
if(v == unf[v]) return v; //집합번호와 학생번호가 같을 때 (처음 상태)
else return unf[v] = find(unf[v]); //집합 번호가 다르다면, 집합번호 탐색
}- 위 상태에서 v = 1일 때 집합번호와 학생번호가 다르기 때문에 1번학생의 집합번호인 2번 find(2)호출
- 따라서 값 2를 받을 수 있다.
unf[v] = find(unf[v])- 집합이 커졌을 때 집합 번호를 찾아가는 과정을 압축시켜 준다.
원더랜드(최소스패닝트리 : 크루스칼 알고리즘, Union&Find 활용)
문제
원더랜드는 모든 도시를 서로 연결하면서 최소의 유지비용이 들도록 도로를 선택하고 나머지 도로는 폐쇄하려고 한다.
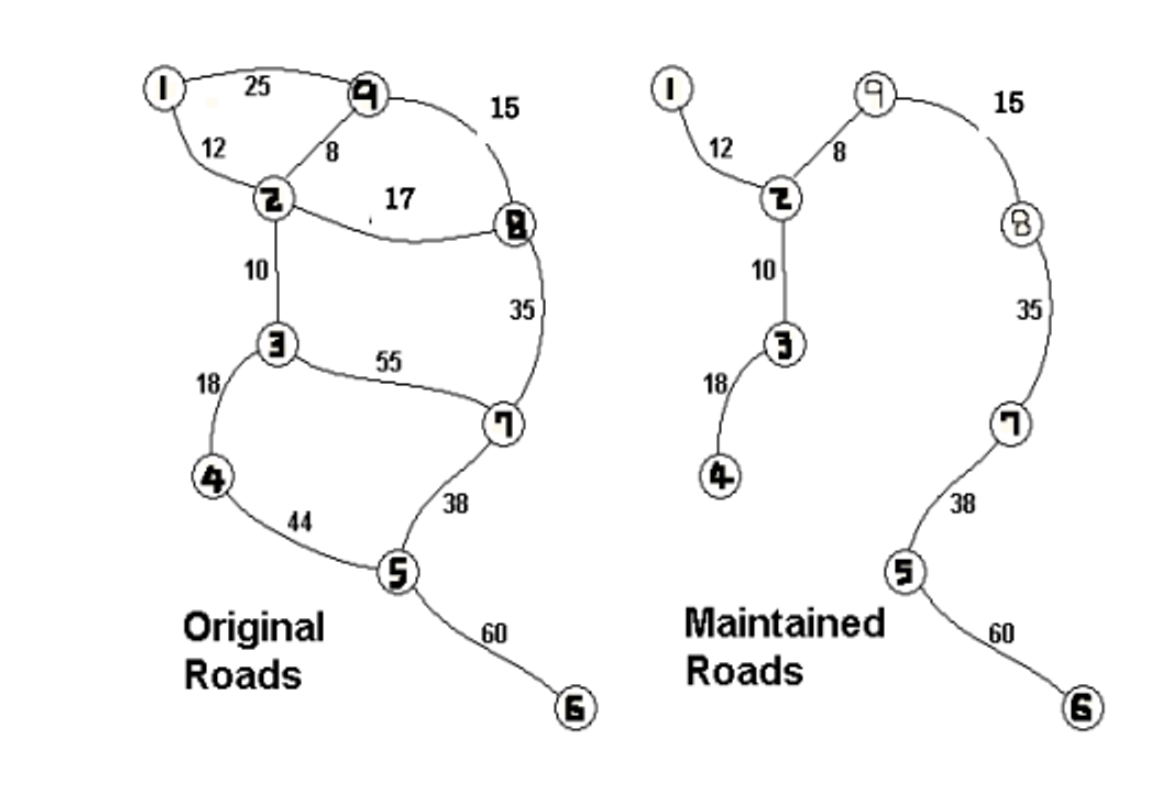
위의 지도는 각 도시가 1부터 9로 표현되었고, 지도의 오른쪽은 최소비용 196으로 모든 도시
를 연결하는 방법을 찾아낸 것이다. (트리는 정점이 n개이면 간선은 n-1개임 무조건 즉 회로가 존재하지 않는다, 그래프는 회로가 존재 → 이를 이용해서 간선 n - 1개가 이어졌을 때 break를 걸어서 while문을 종료하여 시간복잡도를 빠르게 할 수 있다.)
입력설명
첫째 줄에 도시의 개수 V와 도로의 개수 E가 주어진다. 다음 E개의 줄에는 각 도로에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 도시와 B번 도시가 유지비용이 C인 도로로 연결되어 있다는 의미이다.
출력설명
모든 도시를 연결하면서 드는 최소비용을 출력한다.
입력예제 1
9 12
1 2 12
1 9 25
2 3 10
2 8 17
2 9 8
3 4 18
3 7 55
4 5 44
5 6 60
5 7 38
7 8 35
8 9 15출력예제 1
196풀이
- Priority queue를 이용한다 (또는 arraylist를 이용해서 cost기준 오름차순 정렬하여 풀기도 가능)
- (1, 2, 12) (1, 9, 25)같은 입력값을 객체로 만들어 pq에 저장하고 정렬기준을 비용을 기준으로 오름차준 정렬한다(pq에서 꺼낼 때 가장 비용이 적은 간선이 먼저 나오게함)
- pq가 빌때까지 poll하고 poll한 두 도시의 find함수 결과값이 다르다면 union함수로 연결시키고 answer에 cost를 누적시킨다
코드
import java.util.*;
class City implements Comparable<City>{
int x, y, cost;
public City(int x, int y, int cost) {
this.x = x;
this.y = y;
this.cost = cost;
}
@Override
public int compareTo(City o) {
return this.cost - o.cost;
}
}
public class Main {
static int[] unf;
static PriorityQueue<City> pq = new PriorityQueue<>();
static int dis = 0;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int v = sc.nextInt();
int e = sc.nextInt();
unf = new int[v + 1];
for (int i = 1; i <= v; i++) {
unf[i] = i;
}
for (int i = 0; i < e; i++) {
pq.offer(new City(sc.nextInt(), sc.nextInt(), sc.nextInt()));
}
solution();
System.out.println(dis);
}
private static void solution() {
while (!pq.isEmpty()) {
City city = pq.poll();
int a = city.x;
int b = city.y;
if(find(a) != find(b)){
union(a, b);
dis += city.cost;
}
}
}
private static void union(int a, int b) {
int fa = find(a);
int fb = find(b);
if(fa != fb) unf[fa] = fb;
}
private static int find(int v) {
if(unf[v] == v) return v;
else return unf[v] = find(unf[v]);
}
}