1. 시계열 데이터의 특징과 분석 목적

1-1. 시계열 데이터

시계열 데이터란 시간을 통해 순차적으로 발생한 관측치의 집합으로, 이렇게 발생한 연속적인 관측치들은 서로 관련이 있다. 이때 시계열은 반드시 고정된 시간 구간의 관측치여야 한다. 즉 시차(Time lag)이 동일해야 한다. 즉, 불규칙적인 시간 구간이여서는 안된다.

결론적으로 어떤 현상에 대하여 과거에서부터 현재까지의 시간의 흐름에 따라 기록된 데이터를 바탕으로 미래의 변화에 대한 추세를 분석하는 방법. 시간의 흐름을 고려한다는 점이 일반 분석과는 다르다.

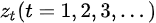
시계열자료는 횡단면자료에서 관측치를 i를 기준으로 측정하는 것과는 다르게 시간 t를 기준으로 측정하는 자료이기에, i가 아닌 t를 사용한다.

이에 횡단면 자료에서의 i.i.d(identically independent distribution)을 가정했던 것과는 다르게 independent 가정을 적용하기에는 어렵다. t시점의 데이터가 t-1 시점의 데이터에 상관성이 존재하기 때문이다.

1-2. 시계열 데이터의 특성

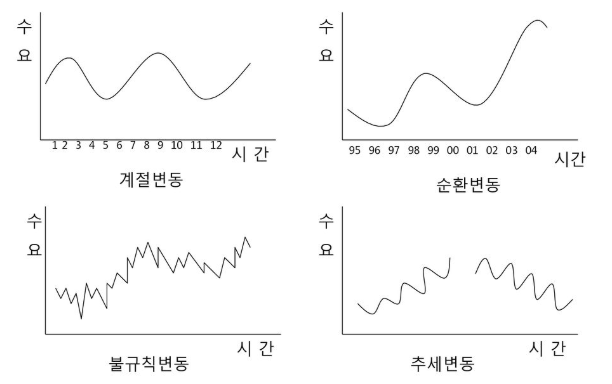
시계열은 크게 아래와 같은 성분으로 이루어진다.

불규칙성분

회귀모형에서의 error term과 같은 것. 시간에 따라 규칙적인 움직임과 무관하게 랜덤한 원인에 의해 나타나는 변동성분을 의미한다.

추세성분

시간이 경과함에 따라 관측값이 지속적으로 증가하거나 감소하는 추세를 갖는 경우의 변동을 의미한다. 이때 추세가 반드시 직선일 필요는 없고, 2차 곡선이나 3차 곡선의 형태로도 나타날 수 있다. 하방경직적같은 특성 이해해야 한다.

계절(순환)성분

일정한 주기에 따라 유사한 패턴이 반복되는 것을 말한다.

• 계절 변동: 1년 안에 월, 분기로 반복되는 패턴
• 순환 변동: 5년, 10년처럼 장기간 동안 간격을 두고 상승, 하락이 주기적으로 반복되는 패턴. 이 때는 데이터가 크며 주로 추세변동과 결합해 분석을 진행한다.

이때, 몇 가지의 성분이 한꺼번에 나타나는 경우에 이러한 패턴들의 확률분포가 일정하지 않을 때 서로 동일하지 않은 분산을 가지면서 이분산성(Heteroskedasticity)이 증가한다. 이에 대해서는 이분산성의 감소를 위한 Log Transformation을 취해주면 이를 감소시킬 수 있다.

시간 t를 x축으로, 시계열 관측값을 y축으로 그리는 그림을 시계열 그림(Time Series plot)이라고 한다.

정상성(Stationary)과 비정상성(Non-Stationary)

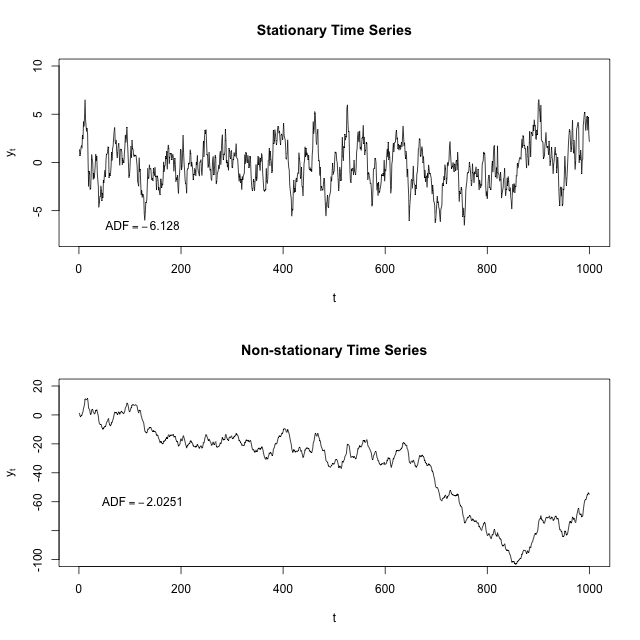
시계열 데이터는 시간의 흐름에 따라 통계적인 특성이 변하지 않고 일정한 추세가 없는 정상성(Stationary) 데이터와 시간에 따라 통계적 흐름이 변화하는 비정상성(Non-Stationary) 데이터로 나눌 수 있다.

정상성 데이터는 평균과 표준펼차가 일정하다는 조건이 선행되어야 분석이 가능하며, 대표적인 예시로 ARIMA 모델이 있다.

비정상성 데이터의 경우에는 분석 시 예측 범위가 무한대이고, variance, autocorrelation 등의 다양한 파라미터를 고려해야 하기에 평균의 정상화를 위한 차분법, 분산의 안정화를 위한 log, 제곱/제곱근 변환 등 방법을 이용하여 정상성 변환을 통해 주어야 예측 범위가 무한대에서 일정 범위로 줄어들고 예측 효과가 증가하면서, 고려해야 하는 파라미터의 수가 감소하여 단순 알고리즘으로 예측할 수 있으며, 이에 overfitting 역시 방지할 수 있다.

정상성(Stationary)과 비정상성(Non-Stationary) 확인법

정상성 및 비정상성을 확인하기 위해서는 Autocorrelation와 Partial auto correlation function을 사용한다. 이들은 현재 시점의 자료와 특정 시점의 차이(lag)를 가진 자료의 상관성을 나타내는 측도이다.

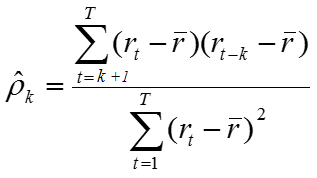
• Auto correlation function
  시점에 따른 Auto correlation을 생각하는 것. 이때 Lag0의 값은 같은 시점과의 상관성을 나타내기에 1 값을 가지므로, 해당 부분은 제외한 후 추세를 파악한다. X축을 lag로, Y축을 ACF로 나타내었을 때 정상 시계열의 ACF는 상대적으로 빠르게 0에 수렴하고, 비정상 시계열은 천천히 감소하는 양상과 함께 큰 양의 값을 가진다.

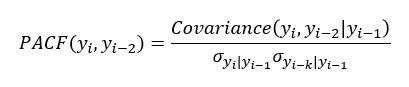
• Partial Auto correlation function
  시점의 차이에 따른 Partial Auto correlation function을 나타낸다. Auto correlation function와의 차이점은 두 시점 내의 구간 값은 고려하지 않고 순수하게 두 시점의 상관관계만을 확인 한다는 것.

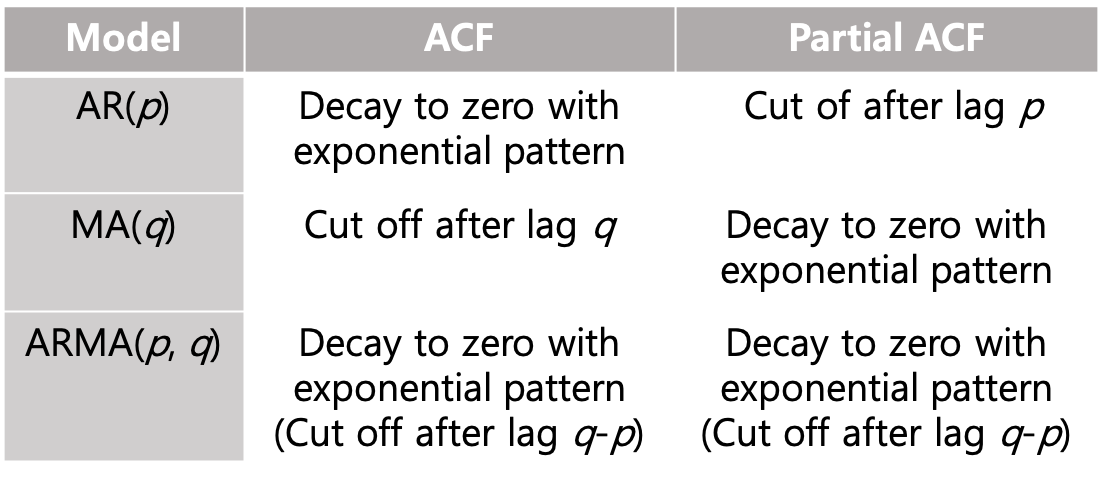
ACF와 PACF의 추세를 활용하여 다음과 같은 모형들을 선택할 때 활용할 수 있다.

원래 Correlation은 두 변수 사이의 관계를 -1 ~ 1 의 값으로 표현하는 척도. Auto correlation은 시계열적 관점으로 time shifted 된 자기 자신과의 correlation을 의미한다.

1-3. 시계열 분석 모형

1. Autoregressive(p) (AR) 모형

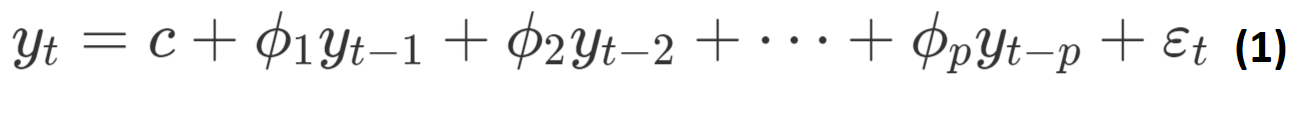
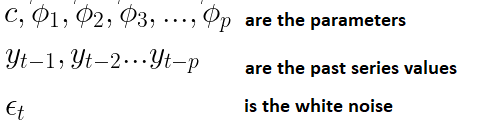
자기회귀 모형(Auto Regressive)로 자기 상관성을 시계열 모형으로 구성한 것. 변수의 과거값의 선형 조합을 이용하여 미래값을 예측하는 방법이다. 자기 자신을 종속변수로 설정하고, 이전 시점의 시계열(lag)을 독립변수로 갖는 모델을 의미한다.

이 경우에는 p를 하이퍼 파라미터로 한다.

2. Moving Average(q) (MA) 모형

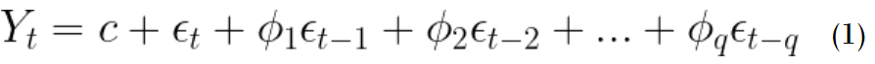
과거의 예측 오차값을 이용하여 미래값을 예측하는 방법. 자기 자신을 종속변수로 설정하고, 해당 시점과 그 과거의 값들과 white noise distribution error ε값을 독립변수로 갖는 모델을 의미한다.

이 경우에는 q를 하이퍼 파라미터로 한다.

3. Autoregressive and Moving Average (ARMA) 모형

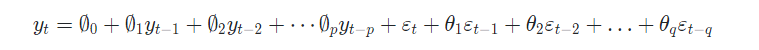
AR모형과 MA모형을 합친 것으로, 자기 자신을 종속변수로 하고, 이전 시점의 시계열(Lag)과 ε를 독립변수로 갖는 모델.

이 경우에는 p와 q를 하이퍼 파라미터로 가진다.

4. Autoregressive Intergrated Moving Average (ARIMA) 모형

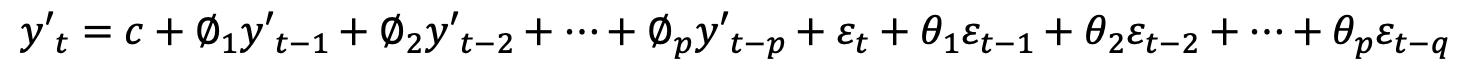
기존 AR, MA, ARMA 모델의 경우 데이터가 Stationary 이어야 했는데, Non-stationary인 경우에는 차분을 통해 데이터를 stationary하게 변형해주어야 한다. ARIMA는 ARMA 모델에 차분을 D회 수행해준 모델이다.

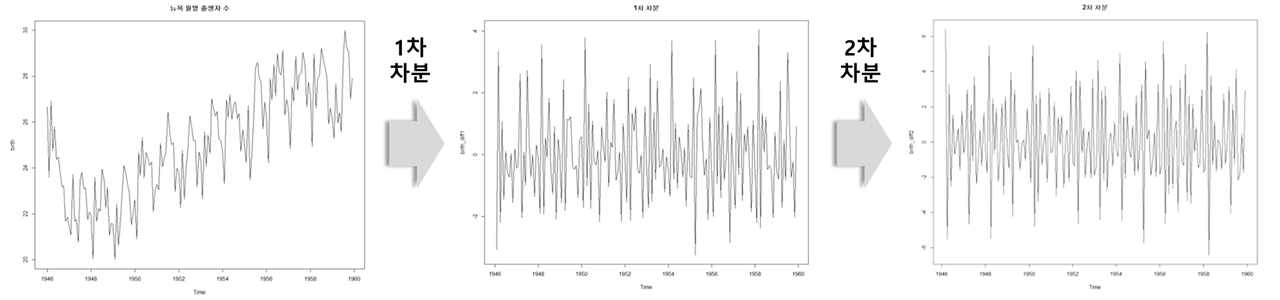
이때, 차분이랑 현 시점 데이터에서 d시점 이전 데이터를 뺀 것이다. 이는 시계열의 수준에서 나타나는 변화를 제거하고 시계열의 평균 변화를 일정하게 만드는 것을 돕는다.