1-1. 변수와 상수

변수(Variable): 값이 고정되지 않아 다양한 값이 들어갈 수 있다.
상수(Constant): 값이 고정되어 변하지 않는다.

인공지능에서 사용하는 모델 중 하나인 신경망에서는 '가중치'라는 개념이 있는데, 컴퓨터는 이 '가중치'를 스스로 학습하며 결정하게 된다.

이때 컴퓨터가 가중치를 학습할 때는 가중치가 '변수'의 역할을 하는데, 학습이 끝나고 해당 가중치를 학습이 끝나고 해당 가중치를 학습 모델에 활요할 때는 '상수'의 역할을 하게 된다. 이처럼 '변수'와 '상수'는 문제 상황을 바라보는 관점에 따라 달라지며, 결국 어떤 것에 관심에 두느냐에 따라 해당 역할이 달라진다.

1-2. 1차식과 2차식

• 1차식은 직선, 2차식은 포물선 모양의 그래프로 표현된다.
• n차식의 가장 큰 차수 앞에 붙은 계수가 양수인지, 음수인지에 따라 그래프의 모양이 달라진다.
• n차식의 그래프가 어떤 모양으로 만들어지는지 이해하고 표현할 수 있다.

항: 숫자나 문자 또는 그 둘의 곱으로 표현되는 식. 이때, 각 항에 변수가 곱해진 횟수를 차수(degree)라고 한다. 이때 두 개 이상의 변수가 곱해진 항의 차수는 각 변수의 지수를 모두 더해주면 된다. 예를 들어 상수만 있고 변수는 없다면 그 항의 차수는 0이다.

계수: 각 항에서 변수에 해당하는 문자를 제외한 부분.

단항식: 1개의 항으로 만들어진 식

다항식: 여러 개의 항이 더하기로 연결된 식

y = ax + b 라는 1차식은 x와 y의 관계를 그래프로 표현한 것으로, 직선 모양이 된다는 특징이 있다. 이때, 계수 a는 직선의 기울기(slope)에 해당하고, b는 x=0일 때의 y값인 절편이 된다.

y = ax^2 + bx + c 라는 2차식에서 a, b, c는 상수로 취급한다. 이러한 2차식에서 x와 y와의 관계를 그래프로 표현할 때, 마치 궤적과 같은 포물선 모양이 된다. 이때 a가 양수이면 포물선이 아래로 볼록하고, a가 음수이면 포물선이 위로 볼록하게 된다.

1-3. 함수의 개념

• 함수는 어떤 입력에 대해 단 하나의 결과를 출력한다.

함수란 어떤 입력값 x에 따라 하나의 출력값 y가 결정된다면 y는 x의 함수라고 말할 수 있으며, 이 관계를 y=f(x)와 같이 표기할 수 있다. 이때, 출력값 y가 두 개 이상이 나온다면 그것은 함수라고 할 수 없다.

프로그래밍에서 말하는 함수는 수학에서 말하는 함수보다 개념이 더 확장되어 어떤 입력값에 대해 참이나 거짓 같은 형태나 문자열 같은 형태도 출력값으로 사용할 수 있다.

1-4. 제곱근

• 제곱을 했을 때 어떤 수가 되는 값을 그 어떤 수에 대한 제곱근이라고 부른다. 제곱근은 √ 기호로 표기한다.

제곱근: 어떤 수 a에 대해 a=b^2을 만족하는 b가 있다면 이러한 b를 a의 제곱근이라고 하며, 실수에서는 양수에 대한 제곱근이 반드시 두 개 존재한다.

1-5. 거듭제곱과 거듭제곱근

a를 p번 곱한 것을 a의 p제곱, 또는 a의 p승이라고 부르며 a^p로 표기한다. 이때, a를 밑(base), p를 지수(exponent index)라고 부른다. 지수는 반드시 정수일 필요는 없고 분수가 되거나 음수가 되어도 상관없다.

p제곱을 하면 a가 되는 수, 또는 p 승을 하면 a가 되는 수를 a의 p제곱근이라고 부르고 a^(1/p)로 표기한다.

1-6. 지수함수와 로그함수

지수함수: a>0, a≠1 이라고 가정할 때, y=a^x로 표현되는 함수를 지수함수라고 한다.

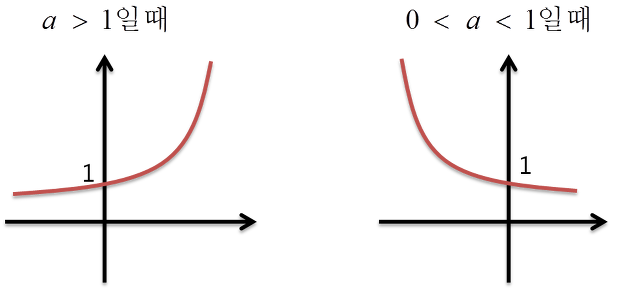
로그함수: 지수와는 정반대의 개념. 어떤 x가 a^y라고 표현될 때의 지수 y를 a의 밑으로 하는 x이 로그라고하며, 기호 log를 사용하여 y=log_(a)x와 같이 표현한다. 이때, x를 진수라고 하는데, a>0, a≠1이고 x>0 이다.

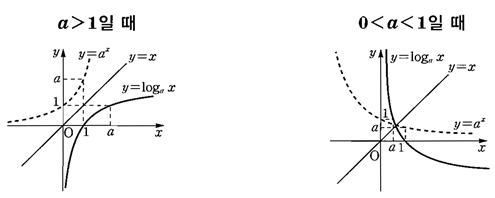
인공지능에서는 가능성을 나타내는 척도로 가능도(likelihood)라는 것을 사용하는데, 이러한 가능도를 다루는 함수를 가능도함수라고 한다. 가능도함수는 식으로만 보자면 확률을 계산하는 것이기에 0이상 1이하의 값을 가지며, 1 이하의 값을 가지기에 계속 곱셈하다 보면 그 값이 점점 작아져서 다루기가 어려워지는데 이런 점을 보완하기 위하여 가능도의 로그를 사용한 로그 가능도함수(log likelihood)함수를 많이 사용한다.

또한, 로그를 사용하면 곱셈을 덧셈으로 표현할 수 있고, 값이 작아지기 때문에 계산이 더 쉬워지는 장점이 있다.

1-7. 자연로그

• e는 2.718...의 값을 갖는 상수이다.
• log_e를 ln으로 표현하기도 한다.
• e^x를 exp x 또는 exp(x)로 표현하기도 한다.

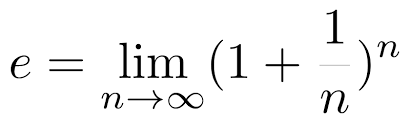
이 수를 네이피어 상수, 또는 자연로그의 밑이라고 부르고 알파벳 e로 표기한다. e를 밑으로 하는 로그를 자연로그라고 하고 log_e대신 ln이라고 쓰기도 한다. 이것이 중요한 이유는 이후 아래와 같은 특징을 이용하여 계산 과정을 간결하게 만들어 줄 수 있기 때문이다.

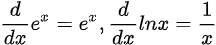
1-8. 시그모이드 함수

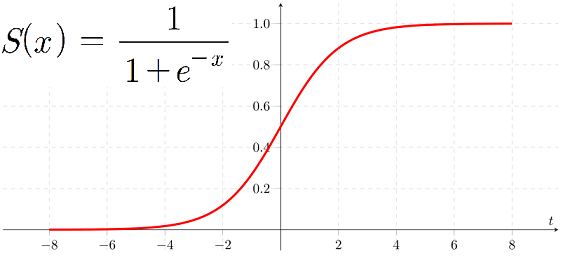
다음과 같이 표현되는 함수를 시그모이드 함수라고 한다.

이때, -x의 계수를 게인(gain)이라고 부르는데, 특별히 a=1일 때의 시그모이드 함수를 표준 시그모이드 함수라고 부른다.

시그모이드 함수는 x가 음의 무한대로 갈수록 분모는 양의 무한대가 되어, 결과적으로 y는 0에 수렴한다. 반대로 x가 무한대로 갈수록 분모는 1에 수렴하여, 결과적으로 y도 1에 수렴하는 특징이 있다.

인공지능에서 시그모이드 함수는 활성화 함수(activation function)으로 사용된다.

이는 인공지능 모델의 표현력을 높이기 위해 사용하는 함수인데, 비선형 분리(데이터의 경계를 곡선으로 분리하는 것)를 할 수 있어 복잡한 데이터들의 관계를 눈에 더 잘 띄게 만들 수 있다. 이에 신경망과 같은 인공지능 모델에서는 이와같은 함수를 많이 사용한다.

1-9. 삼각함수

삼각함수: 각의 크기에 따라 값이 달라지는 함수, 즉 각의 크기가 변수인 함수를 말한다.

• 도수법: 원이 한 바퀴 도는 데 필요한 각을 360도로 표현하는 방법.
• 호도법: 반지름이 r인 원에서 그 반지름과 같은 길이의 호 AB가 있다고 가정할 때, 그 중심각의 크기는 항상 일정하다. 이때의 각을 1라디안이라고 부르고 1rad라고 표기한다.

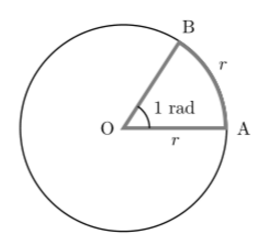
반지름의 길이가 1인 원을 단위원이라고 부르며, 이 단위원을 한 바퀴 도는 데 필요한 호의 길이는 2∏이다. 즉, 호도법에서는 원의 중심각인 360도를 2∏로 표현한다.

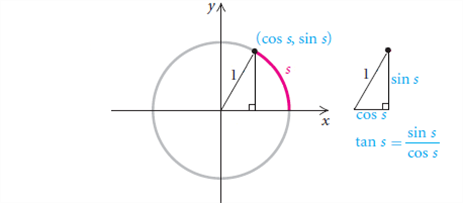
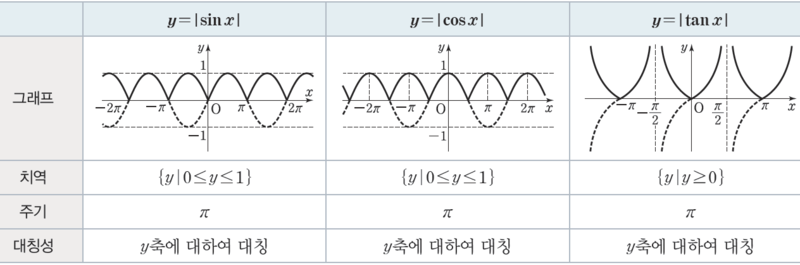
cos의 그래프를 보면 f(-x)=f(x)의 관계인 것을 볼 수 있는데, 이와 같이 y축을 중심으로 좌우가 대칭이 되는 함수를 우함수(even function)라고 한다. 반면 sin의 그래프를 보면 f(-x)=-f(x)의 관계인 것을 알 수 있는데, 이와 같이 원점을 중심으로 점대칭이 되는 함수를 기함수(odd function)이라고 한다.

인공지능 분야에서 삼각함수는 음성 인식을 할 때, 음의 파형을 분석하기 위해 푸리에 변환을 하는데 사용한다. 푸리에 변환은 복잡한 파형을 가진 함수를 삼각함수의 덧셈으로 표현하는 변환 방법이다.

1-10. 절댓값과 유클리드 거리

절댓값: 어떤 수의 절댓값은 그 수와 0과의 수직선상 거리를 의미한다. 이는 |x|이러한 기호로 나타내어 준다.

유클리드 거리: 유클리드 거리는 한 점과 한 점 사이를 자로 잰 것과 같은 거리를 의미한다. 직관적으로 우리가 생각하는 거리의 개념과 같다. 이는 피타고라스 정리를 이용하여 길이를 구한 것과 같다. 이는 ∥x∥이렇게 나타내어 준다.

인공지능 분야에서는 과거의 데이터를 분석하여 최적의 모델을 만드는 학습 단계와, 그렇게 만들어진 모델을 사용해서 새로운 데이터에 대한 카테고리나 수치를 예측하는 추론 단게가 있다.

유클리드 거리는 인공지능 분야의 다양한 알고리즘에서 사용되는데, 그중 하나가 k-NN(k-nearest neighbors algorithm)이다. 이는 지도학습에 해당하는 알고리즘이다. 이는 학습 단계에서 학습된 데이터를 벡터 공간상에 위치시킨 후, 추론 단게에서 새로운 데이터를 같은 공간에 배치한다. 새 데이터가 어떤 카테고리에 속하는지 알기 위해서는 가까이에 있는 k개의 정답 데이터를 보고 추론하게 되는데, 이때 사용하는 것이 유클리드 거리이다.

1-11. 수열

수열: 여러 숫자가 일정한 규칙을 따라 줄지어서 배열된 것

• 항: 수열을 구성하는 숫자 하나하나. 제1항을 초항이라 하며, 마지막 항을 말항이라고 한다.

• 등차수열: 앞, 뒤에 인접한 항과의 차이가 일정한 수열. 그 차이를 공차라고 한다.
  
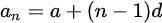
  이때, 등차수열의 합은 초항이 a, 말항이 l, 항의 개수는 n, 초항에서 말항까지의 합이 S라고 할 때, 다음과 같은 식이 성립한다.
  

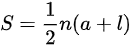
• 등비수열: 앞, 뒤에 인접하는 항의 비율이 일정한 수열. 그 비율을 공비라고 한다.
  
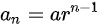
  이때, 초항이 a, 공비가 r, 초항에서 제 n항까지의 합이 S라고 할 때, 다음과 같은 식이 성립한다.
  (1) r≠1
  
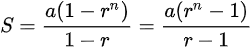
  (2) r=1
  

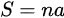
총합(∑) 공식

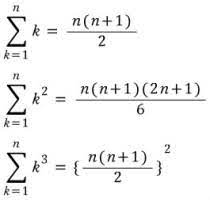
총승(∏) 공식에는 따로 중요한 공식이 없다.

머신러닝 분야에서 주목받는 알고리즘의 하나인 '신경망'은 인간의 신경세포 '뉴련'과 그들의 연결 관계를 인공적으로 흉내 낸 것. 뉴런에 입력되는 값은 여러 개의 '입력값'과 '가중치'의 곱을 모두 더한 다음, 상수를 더 추가한 것과 같다. 이때, 신경망에서는 이런 하나의 모델에서 똑같은 계산이 수백만번 이루어지기도 하기에, 총합 및 총승 공식을 이용하기도 한다.

1-12. 집합과 원소

집합: 어떤 조건을 만족하는 것들을 중복되지 않도록 하나하나 모은 다음, 그것을 통째로 하나의 모둠으로 다루는 것. 기호 ⊂로 포함 관계를 표현한다.

원소: 집합에 들어가는 하나하나의 것들. {a, b, ...} 이때, 괄호 안의 것들이 원소이다. 이는 {x|x에 대한 조건}같은 형태로도 적어질 수 있다. 기호 ∈로 포함 관계를 표현한다.