선형대수를 많이 활용하는 이유는 방대한 양의 데이터나 복잡한 시스템을 비교적 간단하게 표현할 수 있을 뿐만 아니라 컴퓨터로 계산하기도 쉽기 때문이다.

3-1. 벡터

• 벡터를 표기하는 방법에는 하나의 문자로 간단히 표시하거나, 벡터의 성분을 구체적으로 나열하는 방법이 있다.

• 벡터에는 행벡터와 열벡터 두 종류가 있다.

변수란 어떤 형태의 데이터 1개를 담아낼 수 있는 일종의 상자 같은 것. 이때, 수학에서 데이터 여러 개를 한 줄에 담아낼 수 있게 만든 것이 벡터.

벡터를 표기하는 방법은 다음과 같다.

하나의 문자로 나타내는 방법: 소문자를 굻게 표시, 문자의 위에 화살표 표시, 문자에 세로선 장식

구체적인 성분을 나열하는 방법: 행벡터와 열벡터로 표기 가능.

3-2. 덧셈과 뺄셈, 스클라배

벡터에서는 서로 대응하는 성분끼리 덧셈 및 뺄셈을 할 수 있다. 행벡터나 열벡터 상관없이 같은 방식으로 계산을 할 수 있다.

벡터 성분의 수를 차원이라고 한다. 이때 차원이 같아야 덧셈 및 뺄셈을 진행할 수 있다.

덧셈과 뺄셈 외에도 스칼라배(scalar multiple)이라는 계산이 있다. 이는 전체 성분에 스칼라값을 곱셈하면 된다.

인공지능에서 컴퓨터로 언어를 처리하기 위해 단어들을 벡터처럼 취급하는 방법이 있다. word2vec이 이것인데, 이는 단어 하나하나를 일렬로 늘어놓아 벡터를 만드는 것이다.

일단 벡터로 변환하게 된다면 일반적인 벡터 연산처럼 단어들과 덧셈과 뺄셈을 할 수 있게 된다. 예를 들어 "왕" - "남성" + "여성" = 여왕 처럼 연산이 가능하다.

3-3. 유향선분

유향선분이란 방향과 거리를 나타내는 화살표를 말한다.
유향선분의 개념에 입각한다면, 스칼라배는 유향선분의 방향을 바꾸지 않고 길이만 바꾸는 계산이다. 음수로 스칼라배를 벡터에 취해준다면, 이는 '같은 방향인데 길이가 마이너스'라고 간주한다.

a=(1,2), b=(3,1)인 벡터를 간주하였을 때, 이는 결과적으로 a+b=(4,3)만큼 움직인 것이 된다. 다른 관점으로 생각하면 a와 b로 만든 평행사변형의 대각선이 a+b라고 볼 수도 있다.

3-4. 내적

내적은 벡터에서 서로 대응하는 성분끼리 곱한 다음 그것들을 모두 더한 값이다. 이때, 벡터와 벡터의 내적은 스칼라 값이 나오게 되며, 서로 다른 차원의 벡터끼리는 계산을 할 수 없다.

이때, 내적은 다음과 같은 기하학적인 특징으로 정의할 수도 있다.

벡터 a와 b가 이루는 각이θ일 때 <a,b>는 다음과 같이 정의할 수 있다.

이때 각θ는 두 개의 벡터 a와 b를 일치시켰을 때 생기는 각을 말하며, ∣∣a∣∣는 벡터 a의 길이, 즉 유클리드 거리를 의미한다.

3-5. 직교 조건

두 벡터 a,b가 직교한다는 것은 두 벡터가 이루는 각이 90도라는 의미이다. 이는 결국 a,b의 내적 <a,b> = 0이라는 말이기도 하다.

3-6. 법선벡터

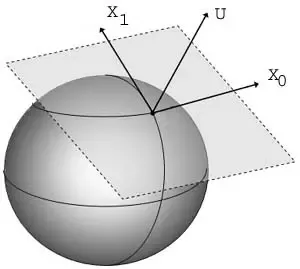
앞서 미분을 하면서는 2차원 곡선에 대한 접선을 다루었으며, 3차원 곡면에 대한 접선은 어떻게 다룰 수 있을까. 구는 3차원 곡면이기에 무수히 많은 접선이 나오는데, 이러한 접선들은 모두 같은 평면위에 존재한다는 공통점이 있다. 이때, 이 평면을 접평면(tangent plane)이라 하고, 접평면과 접하는 구의 점을 접점이라고 한다. 접평면상에 있는 접선들은 무한히 많으므로 일반적인 방법으로는 이 접선들을 다루지 못한다.

이에 이러한 접선들과 직교하는 벡터를 통해 무한한 접선들을 다루는 개념으로써 법선벡터(normal vector)가 존재한다. 즉, 법선벡터는 3차원 곡면에 대한 전체 접선과 직교하는 벡터로 정의할 수 있다. 이때, 하나의 점과 법선벡터가 주어지면 하나의 평면을 정할 수 있다.

3-7. 벡터의 노름

벡터에서는 방향과 이동 거리가 중요한데, 이때의 이동 거리를 노름(norm)이라고 한다.

다음과 같이 벡터 a=(4,3)에 대응하는 유향선분을 그렸을 때, 벡터 a는 오른쪽으로 4만큼 위로 3만큼 움직였으므로, 합계 7만큼 움직였다고 볼 수 있다. 이를 L1 노름이라고 부르는데, 이는 벡터 성분의 절댓값을 모두 더하면 구할 수 있다.

시작점에서부터 목적지까지 직선으로 움직이는 방법도 있다. 위의 a벡터를 생각했을 때 a의 직선 이동 거리는 5가 나온다. 이렇게 유클리드 거리와 똑같이 구하는 거리를 L2노름이라고 한다. 또한 이러한 L2노름은 내적한 값에 루트를 씌우는 것으로도 표현할 수 있다.

인공지능에서 L1노름과 L2노름은 선형회귀 모델의 정규화 항에서 사용한다. 인공지능에서는 학습에 필요한 데이터 세트를 학습 데이터와 테스트 데이터로 분류하는데, 학습 데이터로는 모델을 만드는 데 사용하고, 테스트 데이터는 학습 데이터로 만든 모델을 검증하는데 사용한다.

이 과정에서 모델 계수의 절댓값이나 제곱한 값이 커져 버리면, 주어진 학습 데이터로는 모델이 너무 잘 맞아 떨어지나 오히려 테스트 데이터로 검증할 때는 결과가 나빠지는 과적합(overfitting)이 발생할 수 있다. 이를 피하기 위해서는 선형회귀 모델에 정규화 항을 덧붙여 계수의 절댓값이나 제곱한 값이 너무 커지지 않도록 만들어줘야 한다. 즉, 정규화 항은 계수가 너무 커지지 않게 하기 위한 일종의 패널티나 핸디캡 같은 억제 기능을 한다.

3-8. 코사인 유사도

우리는 이전에 배운 공식들로부터 벡터 a, b의 cosθ값을 구할 수 있게 되었다. 여기서 내적과 L2노름의 식을 조합한다면, cosθ를 다음과 같이 구할 수 있는데, 이렇게 구한 cosθ 항을 코사인 유사도(cosine similarity)라고 표현한다.

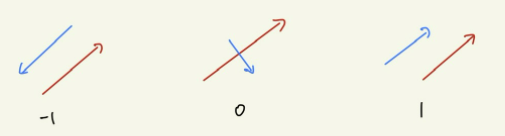
이때, 코사인 유사도의 값은 -1≤ cos(a,b) ≤1 구간 안에 있다. 코사인 유사도가 높다는 것은 벡터가 서로 더 비슷하다는 의미이다. 즉, -1일 때는 두 벡터가 서로 반대 방향으로 평행이고, 0일 때는 직교, 1일 때는 서로 같은 방향으로 평행이다.

인공지능이 텍스트를 분석할 때는 내부적으로 단어나 문장을 벡터로 처리한다. 이때 벡터로 만들어진 단어나 문장들은 서로의 관계성을 파악할 때 코사인 유사도를 사용하며, 높을수록 해당하는 단어나 문장들은 더 가까운 관계라는 것을 나타낸다.

3-9. 행렬의 덧셈과 뺄셈

행렬은 복잡한 계산을 간단한 형태로 표현할 때 사용한다. 벡터가 여러 개의 데이터를 한 줄에 담아낼 수 있게 만들었다면, 행렬은 여러 개의 데이터를 여러 줄에 담아낼 수 있게 사각형으로 만든 것이다. 같은 차원의 벡터를 여러 개 쌓아놓은 것과 같은 모양이다. 행렬은 보통 알파벳 대문자, 즉 A, B, C로 나타낸다.

행렬의 덧셈과 뺄셈은 서로 대응하는 각 성분을 있는 그대로 더하고 빼면 된다.

3-10. 행렬의 곱셈

A = m n 행렬과 B = n l (n차원 열벡터)을 곱하는 것은 m개의 n차원 행벡터와 l개의 n차원 열벡터를 내적하는 것과 같아서 결과적으로 m * l 행렬의 모양이 된다. 이때 A의 열벡터 n과 B의 행벡터 n이 동일해야 연산이 가능하므로, AB=BA와 같은 교환 법칙이 성립하지 않는다.

행렬의 스칼라배는 벡터의 경우처럼 그대로 적용하면 된다.

보통 곱셈을 했을 때, a * b = 0과 같은 결과가 나오면 필연적으로 a나 b중 적어도 하나는 0이지만, 행렬에서는 반드시 그렇다고 단정할 수는 없다. 행렬에도 0과 같은 역할을 하는 것이 있는데, 행렬의 성분 전체가 0인 행렬을 영행렬(zero matrix)라고 한다. 어떤 행렬이나 벡터에 영행렬을 곱하면 그 결과도 꼭 영행렬이나 영벡터가 될 수 있지만, 다만 꼭 영행렬을 곱하지 않더라도 그 결과로 영행렬이 나오는 경우가 있다.

일반적인 곱셈 a * 1 = a 에서와 같이 곱해도 값이 달라지지 않는 1과 같은 행렬도 있다. 왼쪽 위에서 오른쪽 아래 방향으로 대각선상의 모든 성분이 1이고, 그 밖의 성분은 0으로 채워진 정방행렬(square matrix)을 단위행렬(identity matrix)라고 한다. 어떤 행렬이나 벡터에 단위행렬을 곱하면, 그 결과가 달라지지 않고, 원래의 행렬이나 벡터가 그대로 나오는 것이 특징이다. 이러한 조작을 항등사상이라고 한다.

3-11. 역행렬

역행렬은 사칙연산 중 나눗셈과 비슷한 역할을 한다. 보통 우리가 나눗셈을 할 때는 계산의 편의상 나누는 수를 역수(reciprocal)로 만들어 곱할 수 있다. 이러한 역수의 개념을 적용한 것이 역행렬(inverse matrix)이다.

역행렬이 있으려면 일단 정방행렬이어야 하며, 정방행렬이더라도 행렬식(determinant)이 0인 경우에는 역행렬이 존재하지 않는다. 행렬식은 다음과 같이 표기하고 계산한다.

역행렬의 경우에는 다음과 같이 계산할 수 있다.

단 2*2 행렬보다 큰 정방행렬의 역행렬은 이 공식으로는 구할 수 없고, 가우스 소거법(Gaussian elimination)이나 여인자 전개(cofactor expansion)과 같은 방법을 이용해야 한다.

3-12. 선형 변환

선형변환(linear transformation)은 수학적으로 벡터에 행렬을 곱해 또 다른 벡터를 만드는 함수를 말한다. 하나의 벡터 공간에서 또 다른 벡터 공간으로, 벡터의 특징을 유지한 채 변환하는 방법이라고도 볼 수 있다.

표준기저를 먼저 고려해야 하는데, 이는 벡터 공간을 구성하는 기준으로, x축이나 y축, 그리고 z축처럼 일종의 '좌표계'를 정할 수 있는 벡터의 집합을 말한다.

행렬 A역시, 두 개의 열벡터로 다음과 같이 나누어 A = (e1, e2)를 만들 수 있다.

행렬 A에 의한 선형 변환은 다음과 같이 기하학적으로 그릴 수 있다.

다음과 같이, 원래 b_1은 기준점 O로부터 e_x방향으로 3만큼, e_y방향으로 2만큼 움직인 지점이였으나, A를 통하여 Ab_1은 기준점 O로부터 e_1방향으로 3만큼, e_2 방향으로 2만큼 움직인 지점으로 갔다.

즉, 이 행렬의 계산은 벡터를 회전하거나 확대, 또는 축소시킨 것과 같은 효과를 낸다. 그래서 어떤 벡터의 왼쪽에서 행렬 A를 곱한다는 것은 그 벡터를 다른 벡터 공간으로 변환하고 회전하거나 확대, 또는 축소하는 것과 같으며, 이를 달리 표현하면 표준기저(e_x, e_y, ...)에서 다른기저(e_1, e_2, ...)로 변환한다고 표현한다. 이렇게 벡터 공간상에서 벡터를 변환하는 것을 선형 변환 또는 1차변환이라고 한다.

인공지능에서 사용하는 알고리즘 중 '신경망'은 계산하는 과정에서 파라미터와 가중치를 곱한 다음, 그 결과를 모아서 합산하는 처리가 많은데, 이때 파라미터와 가중치를 곱하는 과정을 일종의 선형 변환으로 볼 수 있다.

y = Wx + b 과정에서 Wx가 선형 변환 과정.

3-13. 고윳값과 고유벡터

정방행렬 A가 있고 다음의 식을 만족하는 열벡터 x(단, x≠0)가 존재할 때, λ를 행렬 A의 고윳값(eigenvalue)라 하고, x를 고유벡터(eigenvector)라 말한다. 이때, E는 단위행렬을 말한다.

이 식은 다음과 같이 변환 가능하며, 역행렬을 가진다면 다음과 같이 정리할 수 있다.

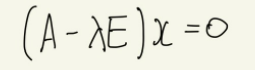
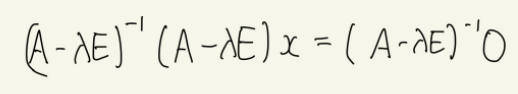
계산 결과, 이 식은 반드시 x=0이라는 자명한 해를 가지나, 이렇게 되어버리면 처음에 가정했던 고유벡터 x가 x≠0이라는 조건과 모순이 되기에, (A-λE)는 역행렬을 가지지 않아야 한다. 이에 고유벡터가 존재하기 위한 조건식은 다음과 같다.

이런 λ의 방정식을 행렬 A의 고유방정식(eigenvalue equation)이라고 한다.

이러한 고유벡터와 고유값의 의미는 선형 변환이 일어났을 때, 벡터가 회전하지 않고 확대나 축소만 할 때, 변화한 벡터의 길이 비율이 고유값이 되고 벡터의 방향이 고유벡터가 된다.

임의의 행렬에 대하여 고유값과 고유벡터를 구하는 방법은 다음과 같다.

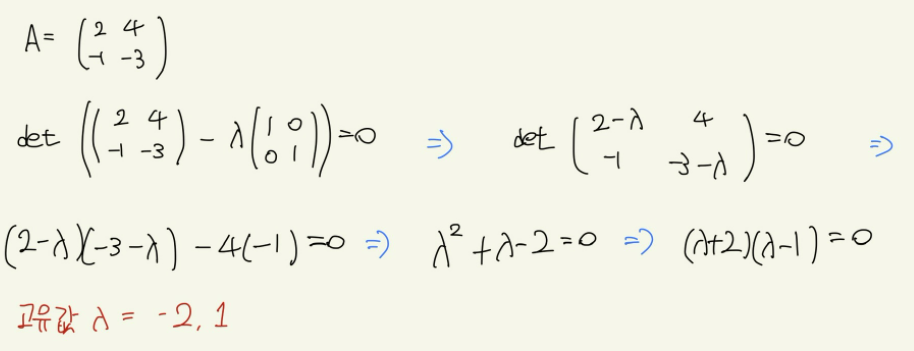
인공지능 알고리즘 중에는 정답 데이터가 없는 비지도 학습이라는 분야가 있다. 비지도 학습에는 주성분 분석(PCA: principal component analysis)라는 기법을 쓰는데, 이는 다차원 데이터를 다루기 쉽게 만들기 위해 2차원이나 3차원으로 압축하는 방법이다.

데이터라 많이 흩어져 있는 분포 상황에서는 문제를 해결하기 위해 고유값과 고유벡터를 사용하는데, 고유값은 어떤 데이터가 가진 특징을 얼마나 잘 설명할 수 있는지 가늠할 때 사용한다. 실제로 기여율(결정계수, coeffient of determination)이라는 것은 각 주성분, 즉 고유벡터에 대응하는 고유값들을 전체 고유값들의 총합으로 나눈 것으로 주성분이 우리가 가진 데이터를 얼마나 잘 설명할 수 있는지를 평가하는 척도로 사용한다.