DP(Dynamic Programming)

동적 계획법 (dynamic programming, DP)

복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법

• 부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용
• 문제의 풀이 결과를 재활용(메모이제이션)함으로써 계산의 효율성을 크게 높이는 알고리즘

DP가 맞는지 판단

최적해의 일부분이 그 부분에 대한 최적해인가?

• 순환식, Optimal Substructure

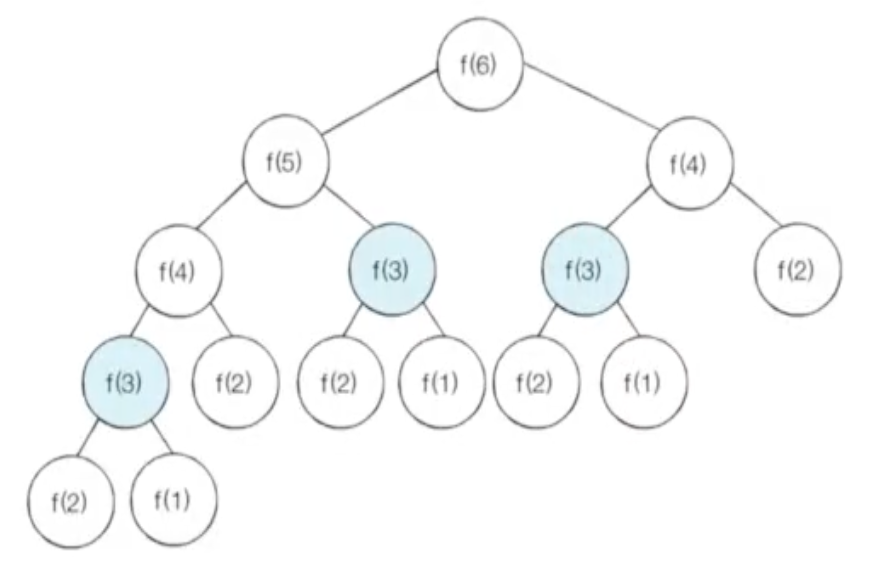
탑다운 방식

큰 문제를 해결하기 위해 재귀적으로 하위 문제를 호출하고, 이미 해결된 하위 문제에 대한 결과는 저장하여 중복 계산을 방지

• 이 방식은 메모이제이션(Memoization)이라고 불린다

피보나치 수열 예제

public class Fibonacci {
	//해결한 하위 문제 결과를 저장할 배열
    private static long[] memo;

    public static long fib(int n) {
        if (n <= 1) return n;
        // 메모 배열에 값이 있으면 해당되는 값을 바로 반환 
        if (memo[n] != 0) return memo[n];
        memo[n] = fib(n - 1) + fib(n - 2);
        return memo[n];
    }

    public static void main(String[] args) {
        int n = 50; // 예를 들어 n이 50이라 가정
        memo = new long[n + 1];
        System.out.println(fib(n));
    }
}

바텀업 방식

가장 작은 하위 문제부터 시작하여 차례대로 상위 문제의 해결책을 구해나가는 방식

• 일반적으로 반복문을 사용하여 구현

피보나치 수열 예제

public class Fibonacci {
    public static long fib(int n) {
        if (n <= 1) return n;
        long[] table = new long[n + 1];
        
        table[0] = 0;
        table[1] = 1;
        
        for (int i = 2; i <= n; i++) {
            table[i] = table[i - 1] + table[i - 2];
        }
        return table[n];
    }

    public static void main(String[] args) {
        int n = 50; // n이 50이라 가정
        System.out.println(fib(n));
    }
}