이분탐색의 상한(upper bound), 하한(lower bound)

이분탐색이 끝나는 지점, 결과를 도출 하는 부분에서 헷갈리는게 많아서 관련 개념에 대해 정리를 해보려한다

https://st-lab.tistory.com/267
참고 포스팅

참고 문제

https://www.acmicpc.net/problem/10816

접근방법

• 고려해야 할 점은 '중복 원소의 개수'를 알아내는 것
• 같은 원소가 있을 때의 값을 알아내야 하기 때문에 몇 가지를 고려하여 작성되어야 한다.

그럼 어떻게 풀이해야 할까?

중복 원소의 왼쪽 끝 값과 오른쪽 끝 값을 각각 알아내는 것이다

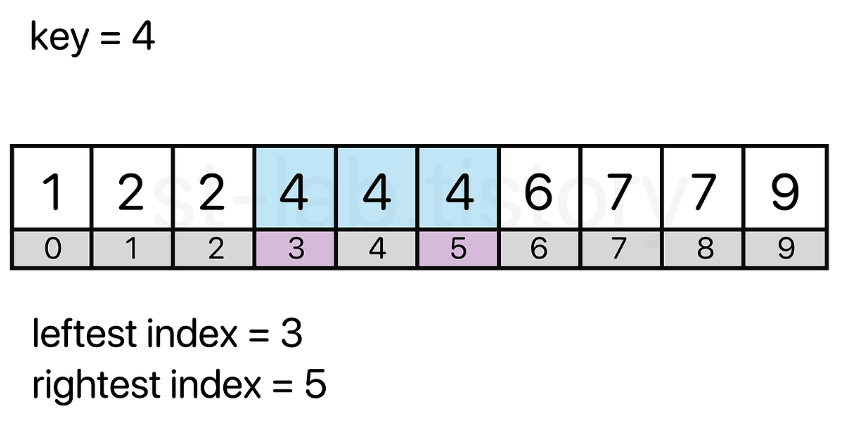
위 배열에서 4라는 값을 찾을 때 4라는 값이 위치하는 "가장 왼쪽의 인덱스와 가장 오른쪽의 인덱스를 얻어내어 구간의 길이를 얻어낼 수 없을까?" 라는 접근 방식인 것이다

이 방식으로 접근하기 위해서 lower_bound 와 upper_bound 를 알아야 한다.

• 자바에서는 각각의 함수를 따로 제공하고 있지 않고 binarySearch() 메소드를 통한 lower_bound 형식의 이분 탐색만을 제공하고 있다.

하한(lower_bound)

하한은 찾고자 하는 값 이상이 처음으로 나타나는 위치를 의미

• 여기서 중요한 점은 '이상'의 값이다 즉,
  왼쪽부터 볼 때 찾고자하는 값이 같거나 큰 경우를 처음 만나는 위치를 의미한다

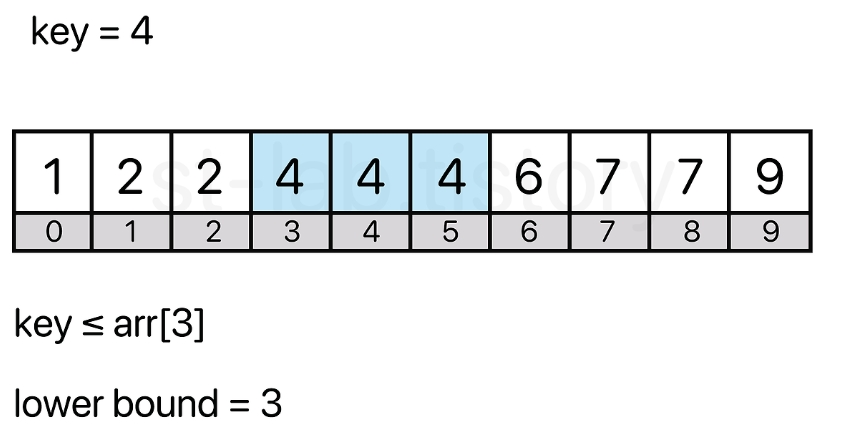
위 이미지에서 처음으로 마주하는 key값 이상을 갖고있는 index는 3이다.

즉, lower bound의 값은 3이 된다

상한(upper_bound)

찾고자 하는 값을 초과한 값을 처음 만나는 위치

• 찾고자 하는 값이 더이상 넘어 갈 수 없는 위치를 의미하기도 해서 상한이라고 한다

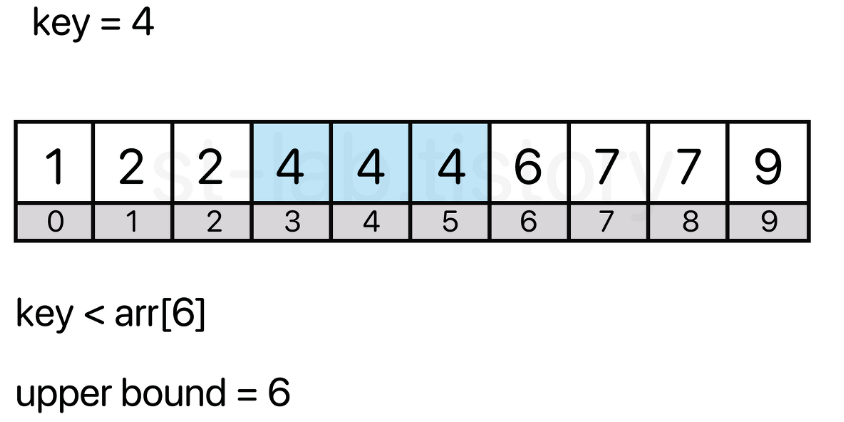
key값인 4를 초과한 처음 만나는 위치(인덱스)는 6이다

찾고자 하는 값보다 큰 값의 위치를 반환하는 것이 바로 upper bound

찾고자 하는 값이 없을 경우의 상한과 하한

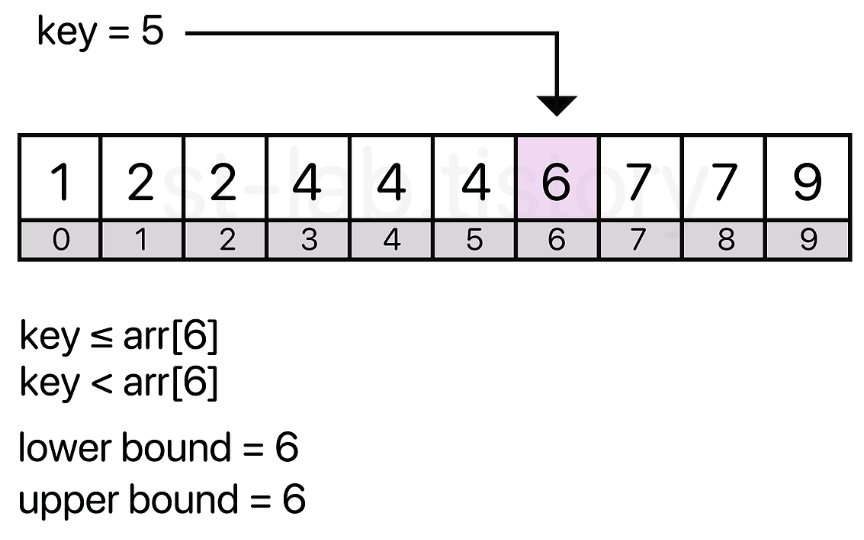
하한과 상한은 각각 어디에 위치하고 있을까?

위에서 설명한 방식 그대로 5이상의 값을 처음 가지는 인덱스가 하한이고,

5초과의 값을 가진 인덱스가 상한이다

위 그림에서는 하한의 위치는 index 6, 상한의 위치는 index 6이다

즉 같은 위치를 가리키게 되는 것이다

두 방식을 어떻게 이용 하는가?

구간의 길이를 알아낼 수 있게 된다

• 즉, 중복원소에 대한 길이 = (상한 - 하한)

만약 원소가 존재하지 않는다면 상한과 하한 모두 같은 인덱스를 가리키고 있을 것이다

-> 구간의 길이는 0이 된다
-> 존재하지 않는 원소를 찾으려 할 경우의 예외 또한 안전하다

두 방식을 적용한 이분탐색의 원리

이분 탐색의 원리는 사실 중앙 위치의 값을 기준으로 key값과 비교를 한 뒤,
상한선(hi)을 내릴 것인지, 하한선(lo)를 올릴 것인지를 결정하는 것이다

내가 헷갈려한 원리

중앙 위치의 값이 앞뒤로도 연속 된 같은 값을 갖고 있다고 할 때, key값과 중앙 위치의 값이 같게 되었다. 이 때, 만약 하한 값을 찾기 위해서는 상한선을 내려야 할까, 하한선을 올려야 할까?

• 하한 값을 찾는 다는 것은 같은 값이 있는 요소들의 가장 왼쪽을 찾아내야한다는 것
  -> 즉, 왼쪽으로 범위를 좁혀야 한다 그러므로 탐색 구간의 상한선을 내려야한다
• 상한 값을 찾기위해서는 하한과 반대로 오른쪽으로 범위를 좁혀나가야 한다
  -> 즉, 탐색 구간의 하한선을 올려야한다.

하한과 상한 구현

private static int lowerBound(int[] arr, int key) {
	int lo = 0; 
    //hi 값을 arr.length로 설정함으로써 배열의 끝까지 탐색할 수 있게 된다
	int hi = arr.length; 
 
	// lo가 hi랑 같아질 때 까지 반복
	while (lo < hi) {
 
		int mid = (lo + hi) / 2; // 중간위치를 구한다.
 
		/*
		 *  key 값이 중간 위치의 값보다 작거나 같을 경우
		 *  
		 *  (중복 원소에 대해 왼쪽으로 탐색하도록 상계를 내린다.)
		 */
		if (key <= arr[mid]) {
			hi = mid;
		}
 
		else {
			lo = mid + 1;
		}
 
	}
	return lo;
}
 
private static int upperBound(int[] arr, int key) {
	int lo = 0; 
	int hi = arr.length; 
 
	// lo가 hi랑 같아질 때 까지 반복
	while (lo < hi) {
 
		int mid = (lo + hi) / 2; // 중간위치를 구한다.
 
		// key값이 중간 위치의 값보다 작을 경우
		if (key < arr[mid]) {
			hi = mid;
		}
		// 중복원소의 경우 else에서 처리된다.
		else {
			lo = mid + 1;
		}
	}
	return lo;
}

이분탐색에서 주의 할 점

현재 문제에서는 중간 값을 구할 때 mid = (lo + hi) / 2 를 해도 문제가 없지만, 사실 값의 범위가 클 경우에는 int overflow가 발생할 수 있다.

• 쉽게 가정해서 lo = 1, hi = 2147483647 (= Integer.MAX_VALUE) 이렇다면,

  • (lo + hi) 과정에서 overflow가 발생하여 -2147483648 가 되고, 여기에 2를 나누게 되어 -1073741824 라는 잘못된 값을 반환할 수 있다.

이러한 경우 어떻게 해결하냐면, 결국 lo와 hi의 중간 값이라는 것은 lo 로부터 hi까지의 거리를 2로 나눈 값을 더한 값이라는 것이다.

• 예를들어

  • lo = 3, hi = 7 이라 할 때, 중간 값은 (3 + 7) / 2 = 5 일 것이다

이렇게 위와 같이 표현 할 수 있지만, 사실 생각해보면, 3 ~ 7까지 거리라는 건 결국 3을 기준으로 7이 얼만큼 떨어져 있는가이다

즉, 3으로부터 4만큼 떨어져있는 지점은 7이라는 것이고, 만약 두 지점의 중간 값이라면, 떨어진 거리의 절반이다

그러면 다음과 같이 표현 할 수 있다

중간 지점 = 시작점 + (거리 차) / 2

이를 수식으로 표현하면

mid = start + ((end - start) / 2)

즉, overflow를 생각한다면, 위와 같이 중간 값을 구해줄 수 있다.