[디지털 영상처리] Chapter 2. Digital Image Fundamentals

해당 포스팅에 사용되는 시각 자료들은 kocw공개 강의-고려대학교 오창현교수님의 디지털 영상처리 pdf자료에서 첨부한 것입니다. http://www.kocw.net/home/cview.do?mty=p&kemId=1094777

1. Intensity

디지털 영상이 밝기의 이산 집합으로 표시되므로, 서로 다른 밝기 레벨들을 구분하는 눈의 능력은 영상 처리 결과를 표시할 때 중요한 고려사항이다.

2. Image Sampling and Quantization

디지털 영상을 만들기 위해서 감지된 연속적 데이터를 디지털 형태로 전환시킬 때 샘플링과 양자화 과정을 거친다.

[그림.1] 샘플링과 양자화 예시

• 디지털 형태로 전환 시키기 위해서는 좌표와 진폭(밝기 레벨) 모두에서 샘플링을 수행해야한다.
• 샘플링(Sampling): 좌표 값들을 디지털화하는 것, 제한된 수의 샘플로 나타낸다.
• 양자화(Quantization): 진폭 값들을 디지털화하는 것, 샘플링 이후 밝기 값들도 이산적 수량으로 전환되어야 하기 때문에 위 예시를 기준으로 8개의 이산 구간으로 나뉜 눈금을 기준으로 8개의 눈금 중 샘플들에 대한 최근접 눈금 값이 부여된다.
• 영상의 맨 위부터 시작하여 이 과정을 한줄씩 적용하면 2D 디지털 영상이 생성된다.

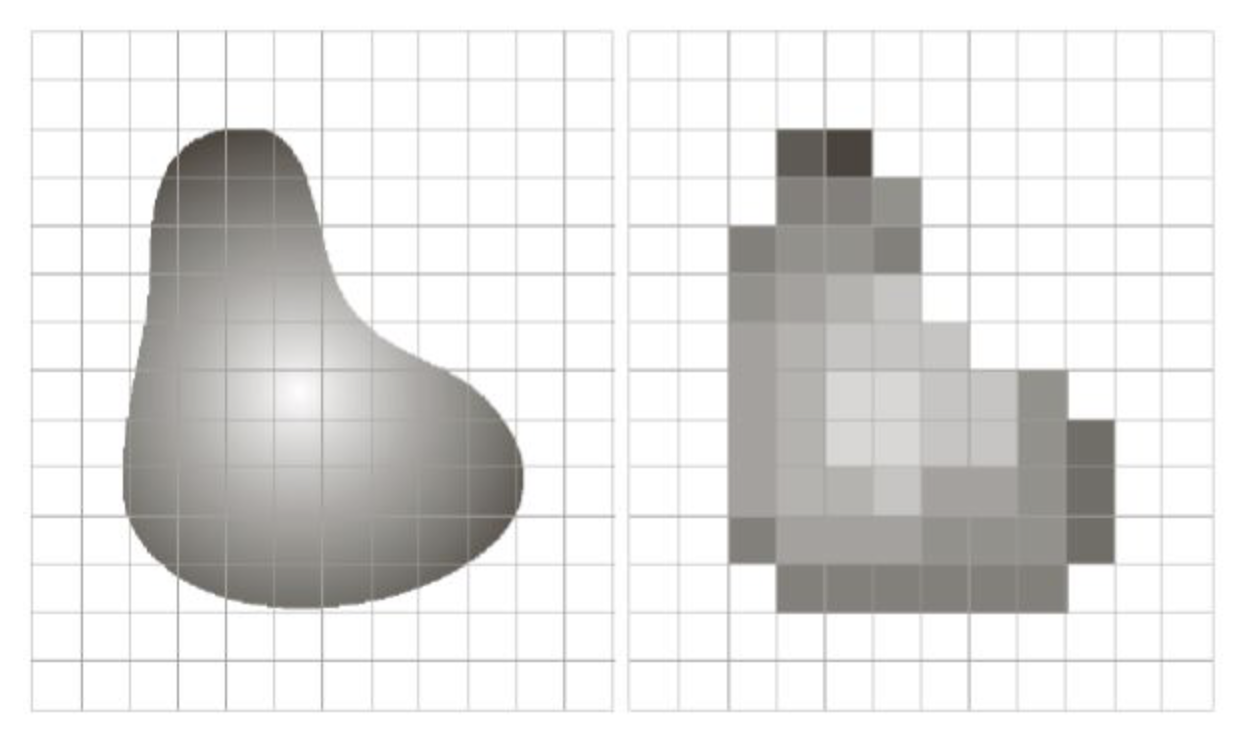
[그림.2] 오른쪽: 샘플링과 양자화 후 영상

3. 디지털 영상 표현

결론적으로 샘플링과 양자화를 거친 영상은 M x N의 2차원 Matrix 형태로 표현되고 처리된다.

• Matrix의 각 요소는 화소라고 불리며 벡터 $V$로 표현할 수도 있다.
• 디지털화 과정에서 M,N 값들과 이산적 밝기 레벨 L 값이 결정되어야한다.
• 밝기 레벨 $L = 2^k$이다.
• 동적 범위: 그레이 스케일에 의해 표현되는 값들의 범위, [$L_{min}$, $L_{max}$]
• 콘트라스트: 영상의 최고 및 최저 밝기 레발 간의 차이
• 동적 범위와 콘트라스트는 비례한다.

- 디지털화된 영상의 크기

• 어떤 영상이 $2^k$개의 밝기 레벨을 가질 수 있을 때 , 이를 "$k$-비트영상"이라고 한다.
  
  
  

4. 공간 및 밝기 해상도(Spatial and Intensity Resolution)

본 절에서는 공간 해상도와 밝기 해상도에 대해서 정리한다.

• 공간 해상도: 이미지를 구성하는 픽셀의 수를 의미하고 픽셀의 개수에 따라 다른 해상도를 보여준다.
• 위에 그림을 보게되면 dpi(인치당 점의 개수)값이 낮을수록 저해상도다.

• 밝기 해상도: Quantization을 수행할 때 밝기 레벨의 수를 어떻게 세분화하느냐에 따라서 해상도가 결정된다.
• 위에 그림은 샘플 수는 일정하게 유지하고 밝기 레벨 수를 256에서부터 2까지 2의 정수 멱승으로 줄인 것이다.

밝기 레벨 N 과 픽셀 수 K가 영상에 끼치는 영향은?

• 위 사진을 대상으로 N과 K를 동시에 바꿔서 생기는 영상 화질에 대한 영향을 실험한 것이다.
• 왼쪽부터 차례대로 레나, 카메라맨, 군중 영상으로 오른쪽으로가면서 더 높은 수준의 디테일을 갖는다.
• 아래 $NK$-평면에 등선호도를 살펴보자.
  
• 위 곡선들을 보면 영상의 디테일이 증가함에 따라 곡선들이 더 수직의 형태를 띄는 경향이 있음을 알 수 있다.
  즉, 디테일이 많은 영상에 대해서는 적은 수의 밝기 레벨들만이 필요하다는 것을 알 수 있다.
  
  
  

5. 영상 보간법(Image Interpolation)

보간법이란 알려지지 않은 부분의 값을 추정하기 위해 알고있는 데이터를 사용하는 과정이다.

• 최근접 이웃 보간법(Nearest neighbor interpolation)
• 이중 선형 보간법(bilinear interpolation)
• 쌍삼차 보간법(bicubic interpolation)

여러 종류의 보간법을 활용해 영상을 재표본화 할 수 있다.
각 보간법에 대한 설명은 추가로 포스팅할 예정이다.

6. 화소 간의 몇 가지 기본적 관계

본 절에서는 디지털 영상의 화소들 간의 몇 가지 관계에 대해서 다룬다.

화소 이웃(Pixel Neighborhood)

• $N_4(p)$는 상하좌우 4개의 이웃을 집합으로 가진다.

• $N_8(p)$는 중심 픽셀 주변 8개의 이웃을 집합으로 가진다.

• $N_D(p)$의 D는 Diagonal를 의미하고 중심 픽셀의 대각선 4개의 이웃을 집합으로 가진다.

인접성, 연결성, 영역, 경계