문제출처 SW Expert Academy
1. 깊이우선탐색(DFS) 개념 (+ 스택)
활용
- 지름길, 미로찾기 등에선 모든 경로를 검색해야함
- 이 때 자주 쓰이는 알고리즘이 DFS(깊이우선탐색)
개념
- 갈 수 있는 곳까지 아래로 내려가며 깊이 탐색
- 더 갈 곳이 없으면 마지막 갈림길 간선으로 돌아온 뒤,
다른 방향의 탐색을 반복해 결국 모든 노드을 방문
-> 마지막 갈림길 간선으로 돌아올 때
후입선출 구조인 스택을 활용
2. 문제소개
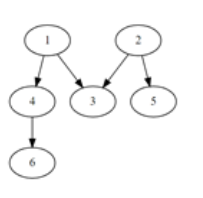
- V개 노드, E개의 간선으로 연결한 그래프가 주어짐
- 시작노드(S), 도착노드(G)가 입력될 때,
길이 연결되어 있으면 1, 없으면 0 을 출력
- 1 에서 6 은 가는 길이 있으므로 1출력
3 .입력값 + 접근
- 테스트 갯수 T, 다음 V(노드)와 E(간선)
-> visit 리스트에 노드갯수만큼 False(방문 전)
-> 방문한 노드는 visit[node] = True
-> 모든 요소 값이 0인 VxV 2차원 배열 graph 정의
- 다음 줄부터 E개 줄만큼 간선의 정보
-> graph에 입력된 간선 연결을 1로 정의
- 마지막 줄엔 출발노드 S, 도착노드 G 입력
-> dfs 함수에 S, G 대입
4. 깊이우선탐색 함수
def dfs(start, end):
stack = []
visit = [False] * (V+1)
stack.append(start)
while stack:
now = stack.pop()
visit[now] = True
for next in range(1, V+1):
if not visit[next] and graph[now][next]:
stack.append(next)
if visit[end]:
return 1
else:
return 0
5. 함수적용
T = int(input())
for tc in range(1, 1+T):
V, E = map(int, input().split())
graph = [[0] * (V+1) for _ in range(V+1)]
for _ in range(E):
start, end = map(int, input().split())
graph[start][end] = 1
S, G = map(int, input().split())
print(f'#{tc} {dfs(S,G)}')

