메모이제이션 (Memoization)

지은·2022년 11월 2일

Algorithm

목록 보기

3/33

메모이제이션 (Memoization)

: 컴퓨터 프로그램이 동일한 계산을 반복적으로 해야할 때, 이전에 계산한 값을 메모리에 저장하여 중복적인 계산을 제거하여 전체적인 실행속도를 빠르게 해주는 기법

동적 계획법(DP; Dynamic Programming)의 핵심이 되는 기술이다.

동적 계획법(Dynamic Programming)

: 크기가 크거나 복잡한 문제를 효율적으로 풀기 위해 작거나 간단한 여러 개의 문제로 나눠서 푸는 방법으로 최적화 문제를 해결하는 알고리즘

작은 부분 문제들을 해결한 후, 그 해들을 이용해서 큰 부분 문제들을 해결하고, 최종적으로 원래 주어진 입력의 문제를 해결하는 알고리즘 설계 기법으로 프로그램의 성능 향상을 기대할 수 있다.

메모이제이션 예제

피보나치 수열

1) 재귀 함수만 이용한 풀이

function fibo(n) {
  // base case
  if(n <= 1) {
    return n;  
  }
  // recursive case
  return fibo(n-1) + fibo(n-2);
};

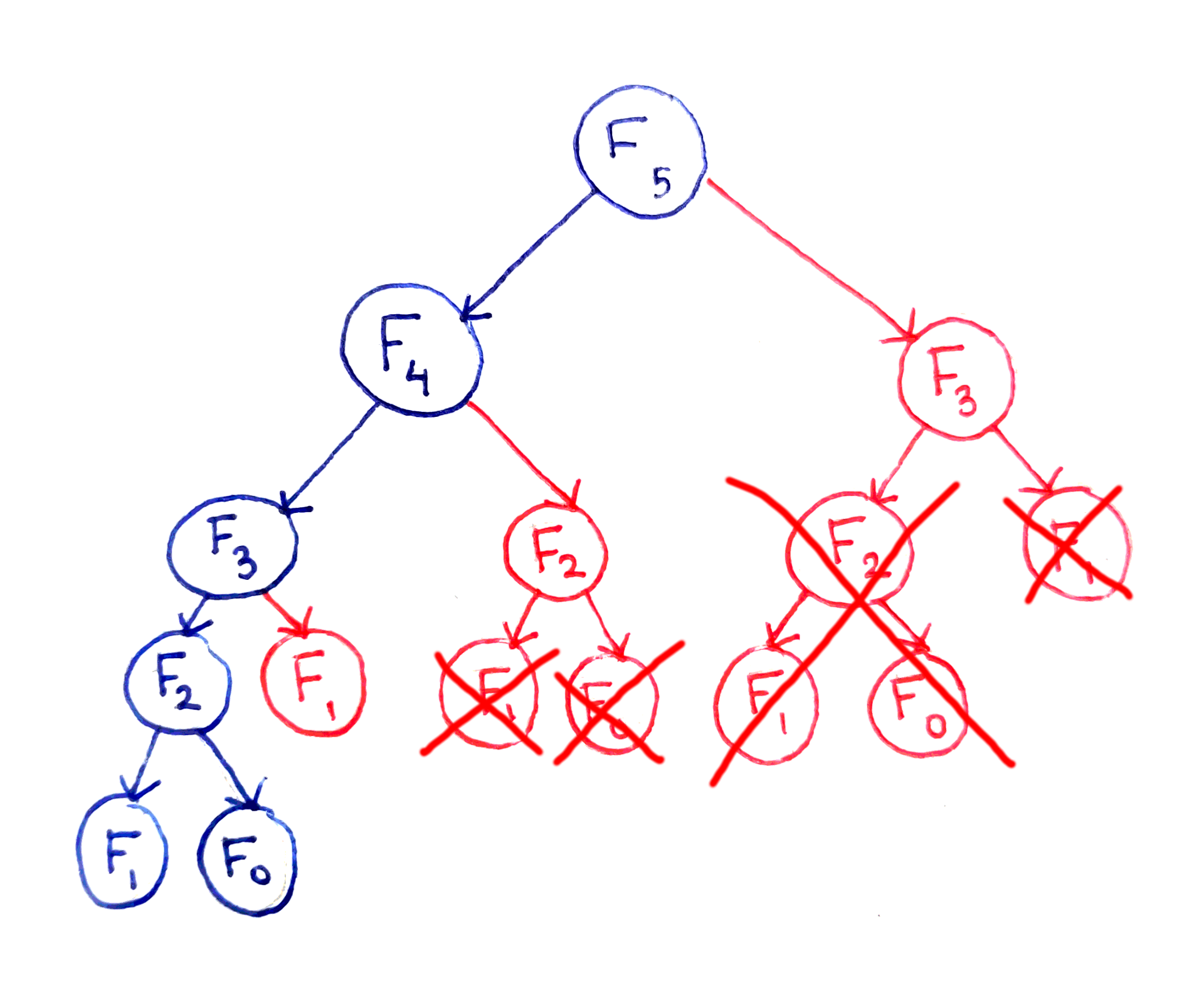
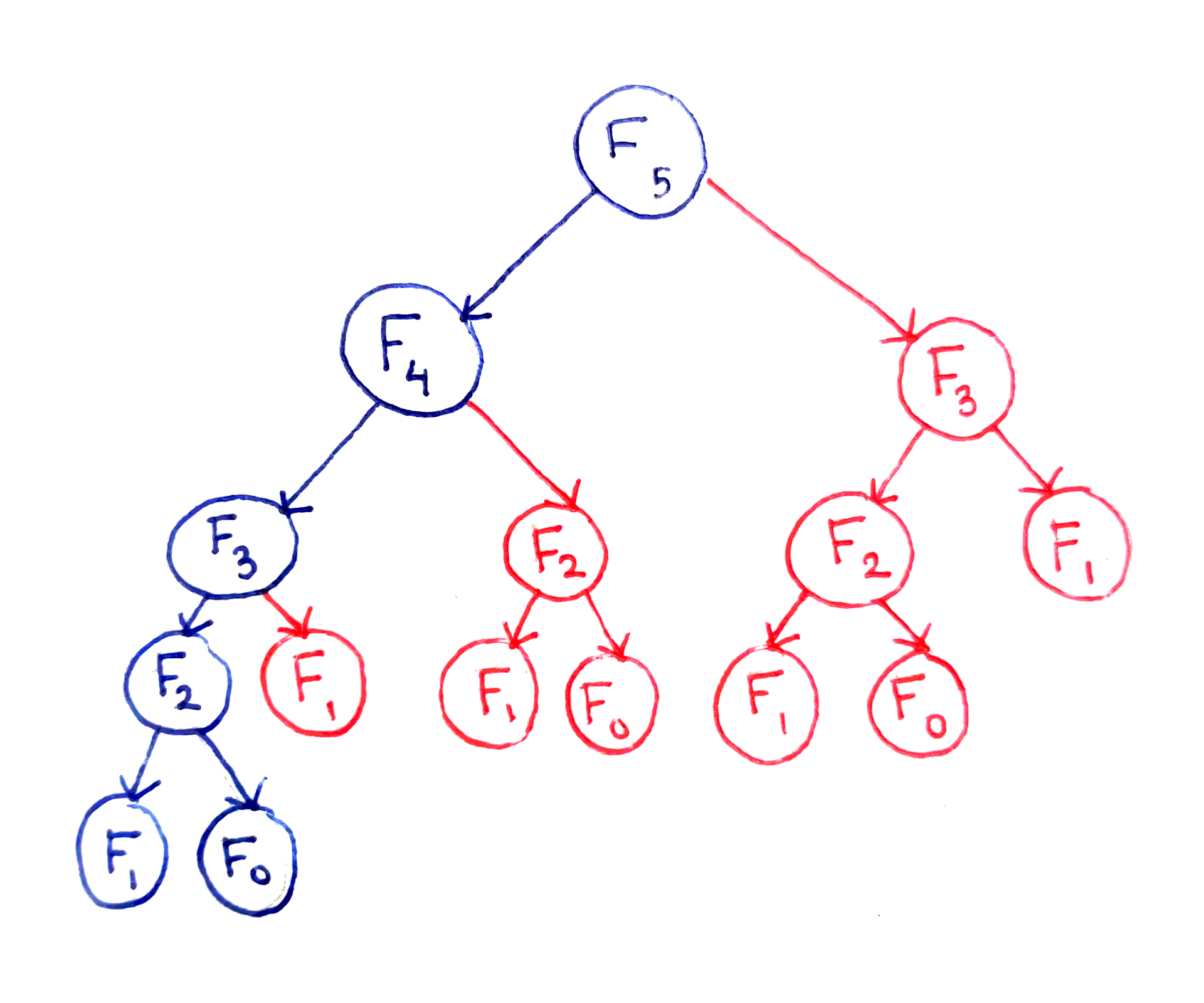
➡️ 층 수가 하나 늘어날 때마다 2가 곱해지고, 총 n개의 층이 있기 때문에 O(2ⁿ)의 시간복잡도(time complexity)를 가진다.

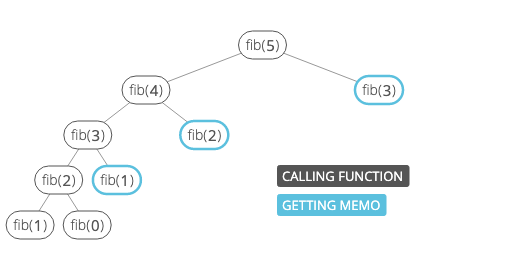
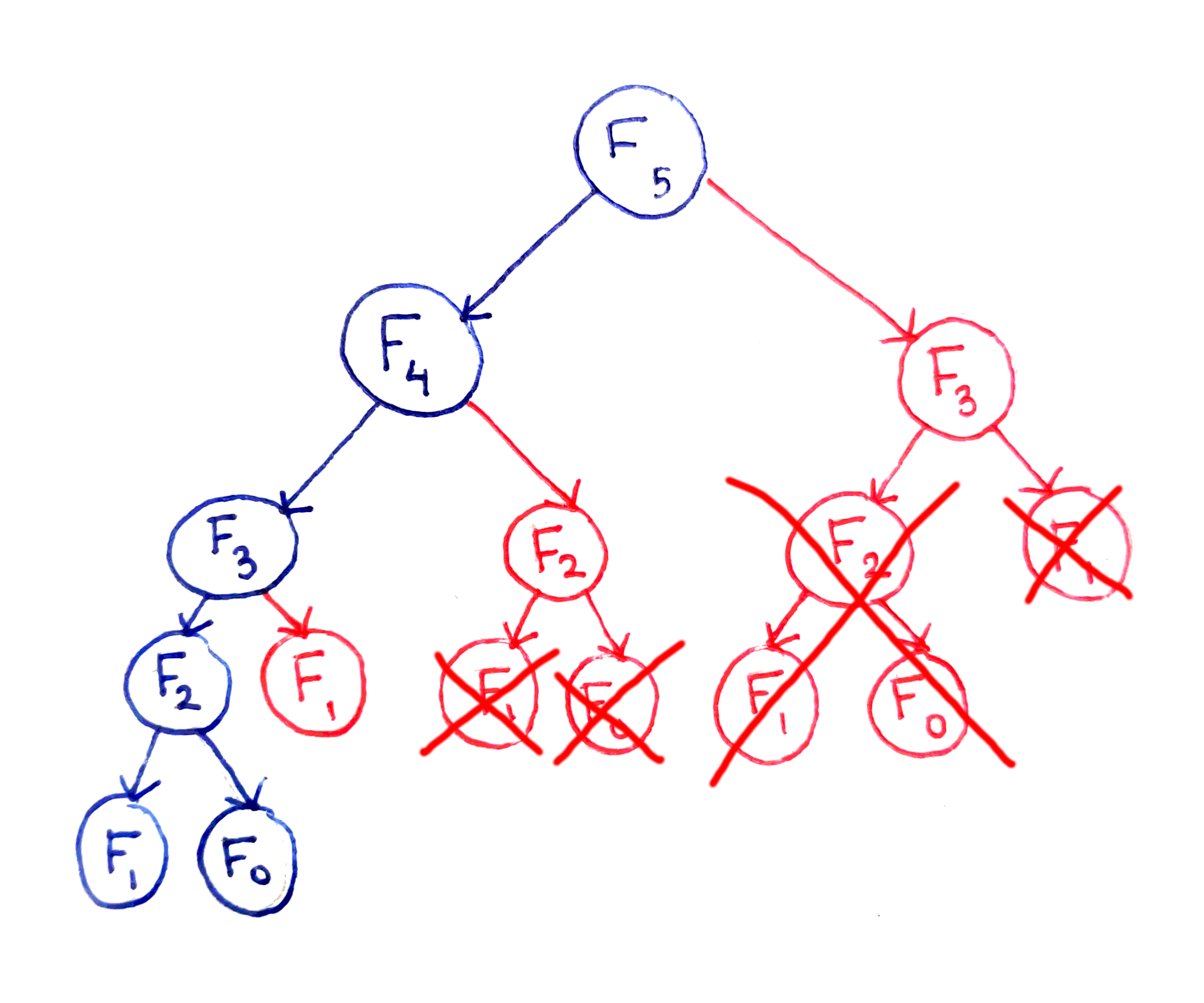
2) 메모이제이션을 사용한 풀이

function fibo(n) {
  const memo = [0, 1];
  function aux(n) {
    // 이미 해결한 적이 있다면, memo배열에 있는 답을 리턴한다.
    if(memo[n] !== undefined) {
      return memo[n];
    }
    // 새롭게 해결해야 하는 경우라면, 문제를 풀고 memo 배열에 추가한다.
    memo[n] = aux(n-1) + aux(n-2);
    return memo[n];
  };
  return aux(n);
};