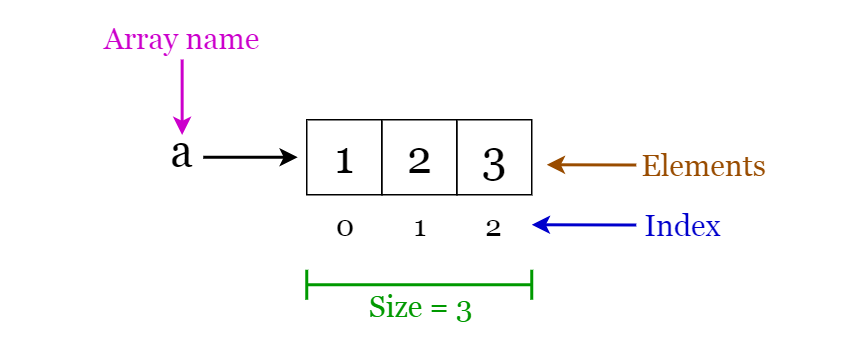
배열 (Array)
: 동일한 데이터 타입의 아이템들을 저장할 수 있는 고정된 크기의 자료구조
- 고정된 크기를 가지며 일반적으로는 동적으로 크기를 늘릴 수 없다.
(하지만 JavaScript, Phython, Ruby와 같은 대부분의 스크립트 언어는 동적으로 크기를 늘리고 줄일 수 있도록 만들어져 있다.) - 배열의 요소를 삭제하면, 해당 index는 당겨지지 않고 빈 자리(
null)가 된다.
배열의 연산
Search
O(1): index를 아는 경우, 배열의 index로 배열의 요소에 접근(random access)할 수 있다.O(n): index를 모르는 경우, 원하는 값을 찾기 위해 배열의 모든 요소를 확인해야 한다.(Linear Search)
Insert, Delete
O(n): 배열의 처음 또는 중간에 요소를 추가/삭제하는 경우,
배열에 요소를 추가/삭제하려면 먼저 기존 배열의 길이 ± 1 의 새로운 배열을 만들고, 기존 배열의 모든 요소를 복사해야 한다.O(1): 배열의 끝에 요소를 추가/삭제하는 경우
🔒 배열은 크기가 고정되어 있기 때문에(메모리를 미리 할당), 배열에 요소를 추가하거나 삭제하는 작업은 바로 수행할 수 없다.
➡️ 배열은 요소를 탐색하는 것은 쉽지만, 요소를 추가하거나 삭제하는 것은 어렵다.
배열의 사용
- 배열 리스트, 힙, 해쉬 테이블, 벡터, 행렬 등 다른 자료구조를 만들기 위한 building block으로 사용된다.
- insertion sort, quick sort, bubble sort, merge sort 등 다양한 정렬 알고리즘에 사용된다.
연결 리스트 (Linked List)
: 각 노드가 데이터와 pointer를 가지고 선형으로 연결되어 있는 방식으로 데이터를 저장하는 자료 구조
- 메모리를 미리 할당하지 않아도 되므로, 유연하게 크기 변경이 가능하다.
- 각 노드는 데이터와 pointer를 가지고 있으며, pointer는 다음 노드를 가리킨다.
- 데이터 : 값이 저장되는 곳
- pointer : 다음 노드의 주소값이 저장되는 곳
- head 노드 : linked list의 가장 첫 번째 요소
- tail 노드 : linked list의 가장 마지막 요소

연결 리스트의 연산
Search O(n)
단순한 선형 검색(Linear Search)을 통해 모든 데이터를 순회하여 요소를 찾는다.
Insert, Delete O(1)
데이터가 삭제되거나 추가되면, 앞 뒤의 노드의 가리키는 pointer만 변경해주면 된다.
➡️ 연결 리스트는 요소를 추가하거나 삭제하는 것은 쉽지만, 탐색하는 것은 어렵다.
연결 리스트의 사용
- 컴파일러 디자인에서 symbol table management에 사용된다.
- 프로그램 간에 Alt + Tab으로 이동하는 기능에 사용된다.
연결 리스트의 종류
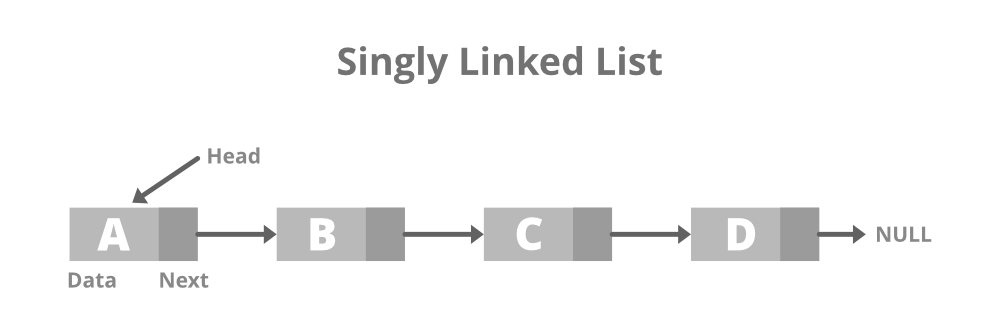
1. Singly Linked List
- 각 노드 당 1개의 pointer를 가지고 있으며, pointer는 다음 노드의 위치를 가리킨다.
- tail은 가장 마지막이므로 다음을 가리키는 pointer를 가지지 않는다.
- 한 방향으로 데이터를 순회할 수 있다.
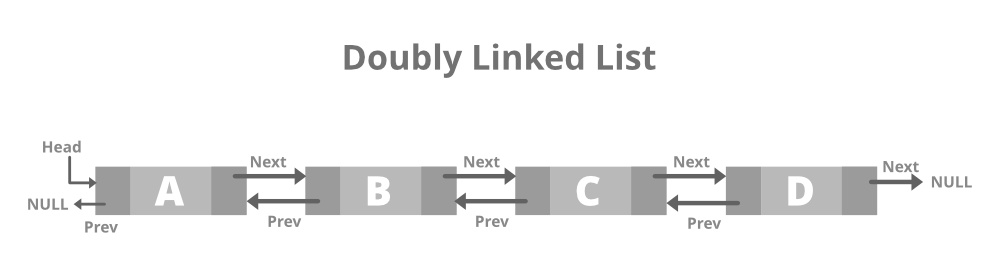
2. Doubly Linked List
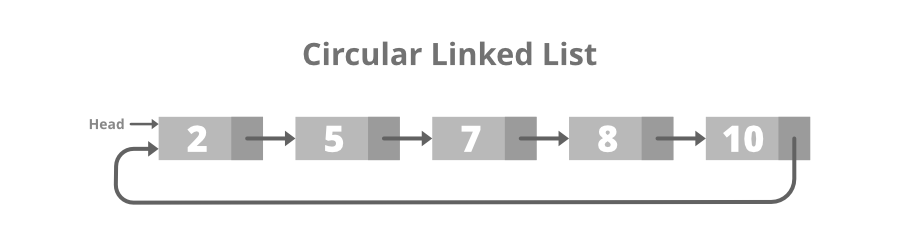
3. Circular Linked List
JavaScript로 단일 연결 리스트 구현하기
단일 연결 리스트는, 요소인 Node 클래스와 SinglyLinkedList 클래스로 구성된다.
// Node 클래스를 만든다.
class Node {
constructor(value){
this.value = value;
this.pointer = null; // Node는 값과 포인터 속성을 가진다.
}
}
// SinglyLinkedList 클래스를 만든다.
class SinglyLinkedList {
constructor() {
this.head = null;
this.tail = null; // SinglyLinkedList는 head와 tail 속성을 가진다.
}
// 찾기 메소드
find(value) {
let currentNode = this.head; // currentNode라는 변수를 생성하고, head 요소를 담는다.(head부터 시작)
while(currentNode.value !== value) { // currentNode는 값(value)을 찾을 때까지 반복문을 순회하며
currentNode = currentNode.next; // 값을 찾을 때까지 다음 노드로 넘어간다.
}
return currentNode; // 값을 찾으면, 반복문을 종료하고 해당 요소를 반환한다.
}
// 맨 앞에 추가 메소드
append(newValue) {
const newNode = new Node(newValue); // 값을 받아서 새로운 노드를 생성한다.
if(this.head === null) { // head가 비어있는 경우, 연결 리스트가 비어있다는 뜻이므로
this.head = newNode; // 새로 생성된 노드가 head와 tail이 된다.
this.tail = newNode;
} else { // head가 비어있지 않은 경우,
this.tail.next = newNode; // 기존 tail의 포인터가 새로 생성된 노드를 가리키게 한다.
this.tail = newNode; // 새로 생성된 노드가 tail이 된다.
}
}
// 중간에 추가 메소드
insert(node, newValue) {
const newNode = new Node(newValue); // 값을 받아서 새로운 노드를 생성한다.
newNode.next = node.next; // 생성된 노드가 입력 받은 노드의 다음 노드를 가리키게 한다.
node.next = newNode; // 입력 받은 노드가 생성된 노드를 가리키게 한다.
// ➡️ 생성된 노드가 중간에 끼워지게 된다.
}
// 삭제 메소드
remove(value) {
// 삭제할 노드의 이전 노드를 찾기 위해 prevNode라는 변수를 생성한다.
let prevNode = this.head; // head 부터 시작해서 찾기..
while(prevNode.next.value !== value) {
prevNode = prevNode.next;
} // 삭제할 노드를 찾아야하기 때문에 선형 시간 O(n)이 소요된다.
if(prevNode.next !== null) {
prevNode.next = prevNode.next.next; // 이전 노드가 다음의 다음 노드를 가리키게 한다.
}
// ➡️ 중간 노드는 아무런 노드와 연결되지 않기 때문에 자연스럽게 삭제된다.
// 해당 노드는 나중에 가비지 컬렉션을 통해 메모리상에서 제거된다.
}
}배열과 연결 리스트의 차이
메모리 차이

배열
순차적인 데이터가 들어가게 메모리를 연속적으로 사용
연결 리스트
순차적이지 않기에 데이터가 퍼져있다.
이렇게 퍼져있는 메모리 영역을 알기 위해 포인터를 사용하여 각 영역을 참조한다.
요소의 추가 / 삭제
배열

배열의 요소를 추가/삭제하기 위해서는 선형 시간 O(n)이 소요된다.
요소를 추가할 자리를 만들거나/삭제된 요소의 공백을 메꾸기 위해, 뒤의 요소들을 모두 당겨야하기 때문이다.
연결 리스트
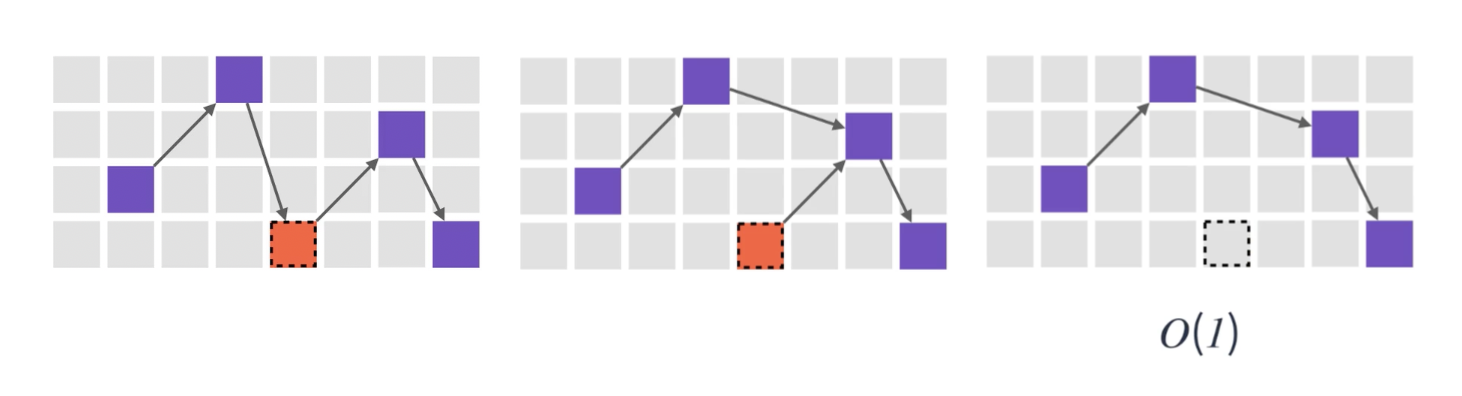
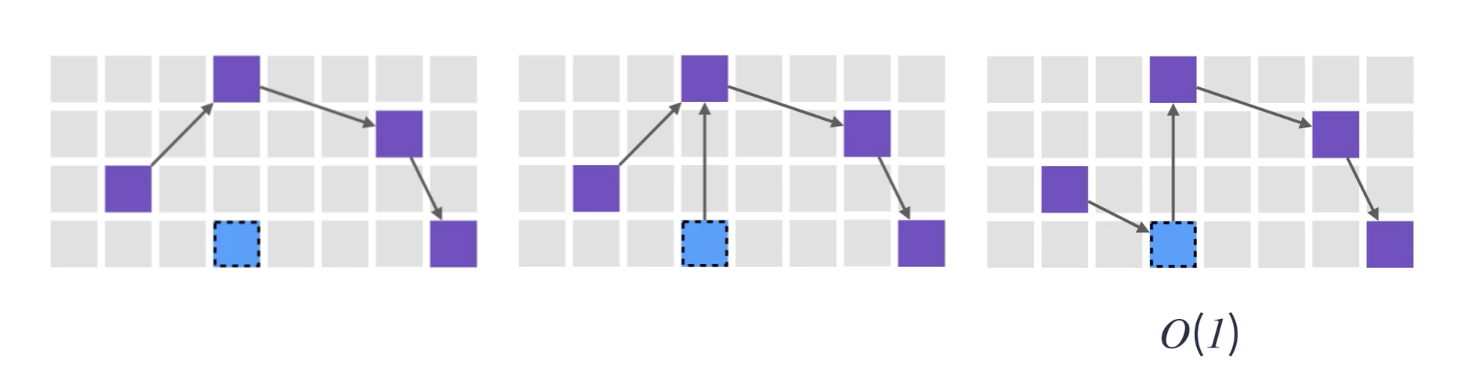
연결 리스트의 요소를 추가/삭제 로직은 상수 시간 O(1)밖에 소요되지 않는다.
정리
- 빠른 접근이 요구되고, 데이터의 추가/삭제가 적을 때 ➡️ 배열 사용
- 데이터의 추가/삭제가 잦고, 검색 빈도가 낮을 때 ➡️ 연결 리스트 사용
이 글은 다음 링크를 참고하여 작성한 글입니다.
8 Common Data Structures every Programmer must know
https://fomaios.tistory.com/entry/DataStructure-연결리스트에-대해-알아보자Linked-List