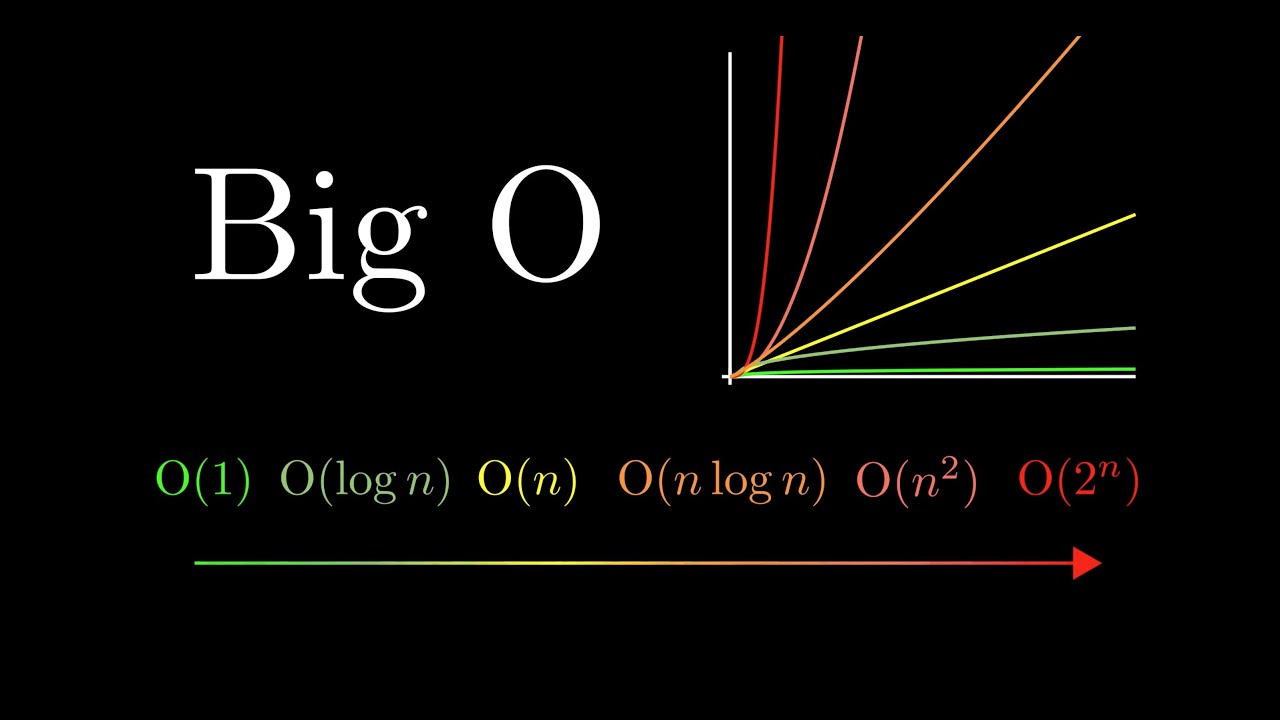
프로그램의 성능을 측정할 때 고려해야하는 것들

• 입력으로 들어오는 데이터의 크기
• 프로그램이 동작하는 하드웨어의 성능
• 프로그램을 실행하고 관리하는 운영 체제의 성능
• 프로그램을 빌드하는 컴파일러의 성능
• 비동기 로직
  ...

➡️ 이러한 다양한 요인이 프로그램의 성능과 실행 시간을 결정하므로, 프로그램의 성능을 정확하게 파악하는 것은 불가능하다.

따라서 절대적인 시간(분, 초)을 측정하는 것이 아닌, 상대적인 표기법으로 프로그램의 성능을 표현하기로 했다.

---

시간복잡도 (Time Complexity)

: 알고리즘의 실행 시간을 알고리즘 수행에 필요한 스텝(step)의 수로 정의하고,
실행 시간을 점근적 표기법으로 단순하게 표현한 것

점근적 표기법(Asymptotic Notation)

: 알고리즘 수행 시간을 표기하기 위해, 필수적인 부분에 집중하고 불필요한 상세들은 무시하는 표기법

1. 계수 무시

for(let i = 0; i < n * 6; i += 1) {
  // ...
}

위의 알고리즘의 시간복잡도는 6 O(n)이지만, 그냥 O(n)으로 표기한다.
n이 무한에 가까워질수록 계수의 크기는 의미가 없어지기 때문이다.

2. 가장 큰 항 외에는 무시

for(let i = 0; i < n; i += 1) {
  // ...
}

for(let i = 0; i < n; i += 1) {
  for(let j = 0; j < n; j += 1) {
    // ...
  }
}

위의 알고리즘의 시간복잡도는 O(n² + n)이지만, O(n²)로 표기한다.

3. 상수항 무시

• O(n² + 126) ➡️ O(n²)
• O(3n - 30) ➡️ O(n)
• O(3 log n) ➡️ O(log n)

---

시간 복잡도를 나타내는 대표적인 표기법으로는 Big-O 표기법이 있다.

Big-O notation

: 입력값(n)이 증가함에 따라 연산을 처리하는 데 소요되는 시간의 증가율을 그래프로 나타낸 것

• 이때, 알고리즘의 실행 시간은 완료까지 걸리는 절차(step)의 수이다.
• Big-O 표기법은 프로그램이 실행되는 과정에서 소요되는 최악의 경우의 시간을 나타낸다.

Big O 표기법의 상대적인 성능을 비교한 그래프

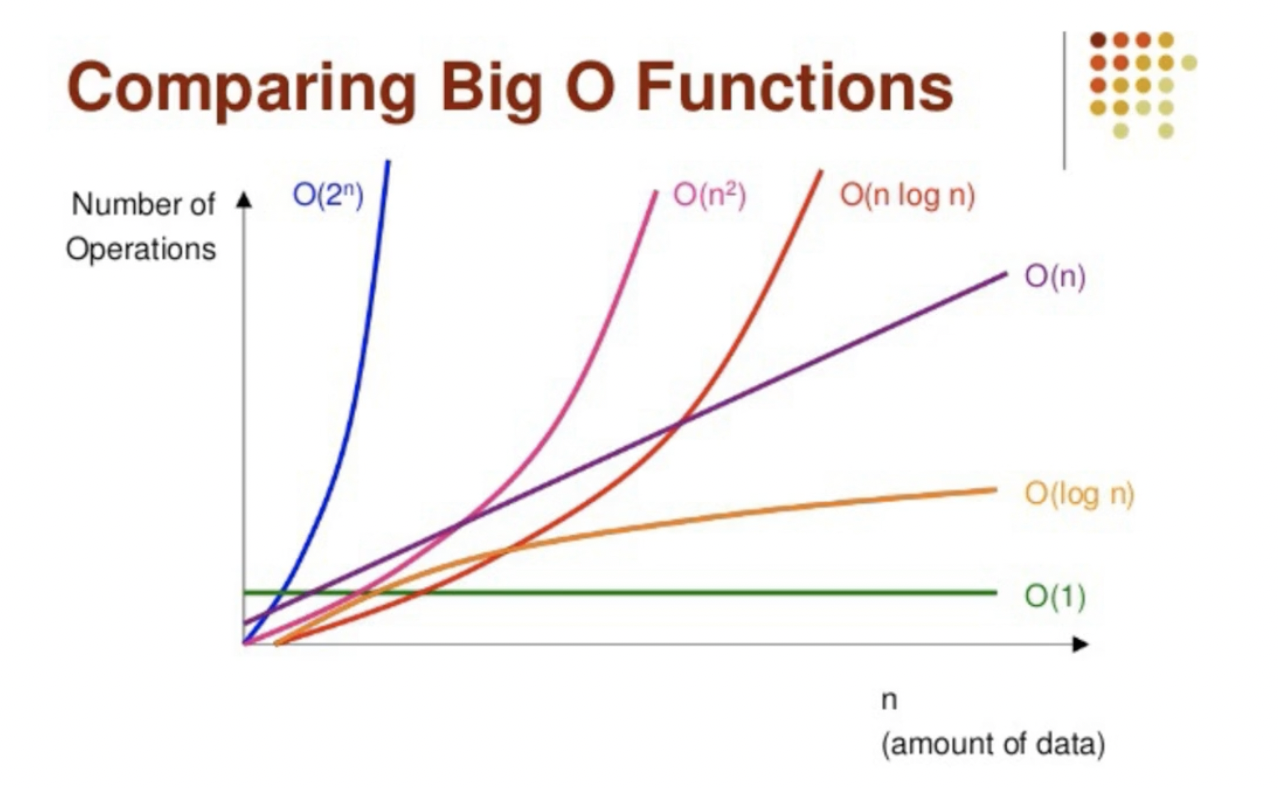
O(1) < O(log₂ n) < O(n) < O(n log₂ n) < O(n²) < O(2ⁿ) < O(n!)
(여기서 log의 밑은 2이다. 컴퓨터 과학에서 log의 밑을 생략하면 밑이 2라고 생각하면 된다.)

상수 시간 < 로그 시간 < 선형 시간 < 선형 로그 시간 < 이차 시간 < 지수 시간 < 팩토리얼 시간

---

O(1)

상수 시간(constant time)
: 입력값(n)의 크기 증가와 관계 없이 실행 시간이 동일하다.

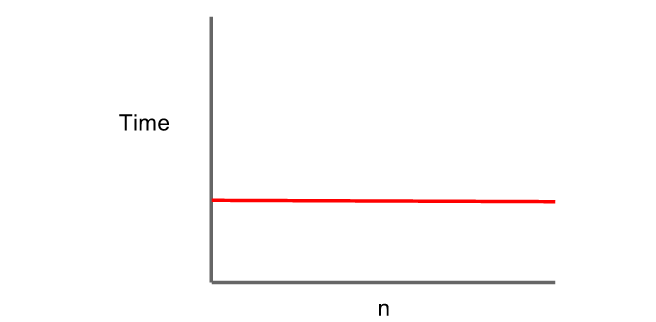
• 입력값(n)의 크기와 관계 없이 동일한 수의 스텝이 필요하다.
• 이 알고리즘에서는 입력값이 10개이든, 100개이든 동일한 스텝으로 출력값을 얻어낼 수 있다.

예시)

function printFirstItem(arr) {
	console.log(arr[0]);
}

---

O(log n)

로그 시간(logarithmic time)
: 입력값(n)의 크기가 증가함에 따라 매 실행 시간이 1/2 줄어든다.

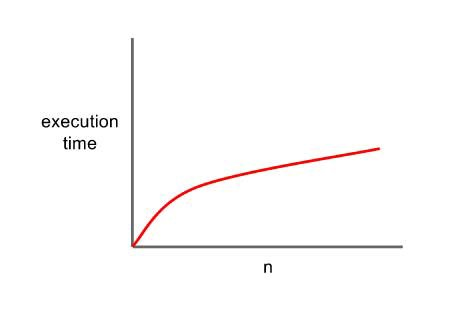
• 상수 시간복잡도O(1)보다는 빠르고, 선형 시간복잡도O(n)보다는 느리다.
• 이진 검색 알고리즘(Binary Search)은 O(log n)의 시간복잡도를 가진다.
  • 이진 검색에서는 원하는 값을 탐색할 때, 매 스텝마다 절반의 아이템을 없앤다.
  • 따라서 입력값이 2배가 되어도 작업을 수행하는 데 필요한 스텝은 1씩만 증가한다.
    

예시)

for(let i = 1; 1 <= n; i *= 2) {
  // ...
}

---

O(n)

선형 시간(linear time)
: 입력값(n)의 크기가 증가함에 따라 실행 시간 또한 같은 비율로 증가한다.

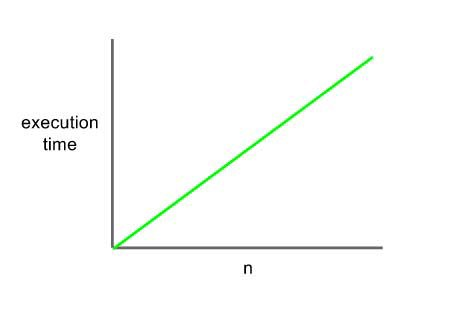
• 입력값이 증가함에 따라 스텝의 수도 증가한다.
• 입력값이 10개라면 10번의 스텝,
  입력값이 100개라면 100번의 스텝이 필요하다.

예시)

for(let i = 0; i < n; i += 1) {
  // ...
}

---

O(n log n)

선형 로그 시간(linearithmic time)
: 입력값(n)의 크기가 증가함에 따라 실행 시간이 n log n만큼 증가한다.

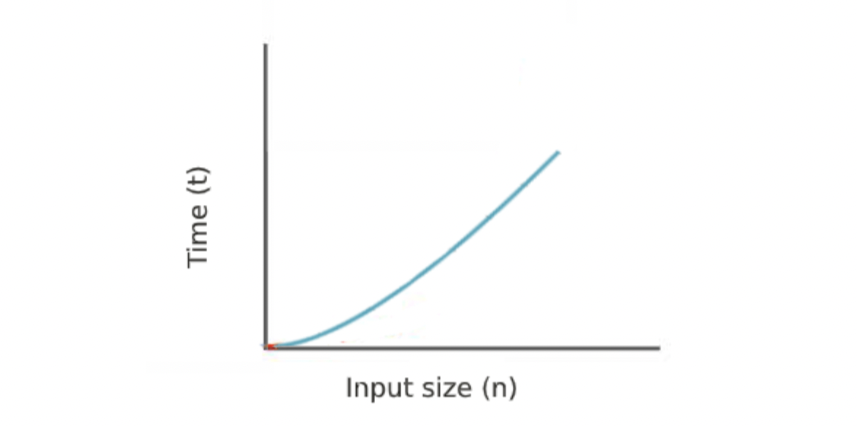
예시)

for(let i = 0; i < n; i += 1) {
  for(let j = 1; j <= n; j *= 2) {
    // ...
  }
}

O(n log n)의 시간복잡도를 가지는 알고리즘

• 병합 정렬(Merge Sort)
• 힙 정렬(Heap Sort)
• 퀵 정렬(Quick Sort) - 최악의 경우 O(n²)의 시간복잡도를 가진다.

---

O(n²)

이차 시간(quadratic time)
: 입력값(n)의 크기가 증가함에 따라 실행 시간이 제곱만큼 증가한다.

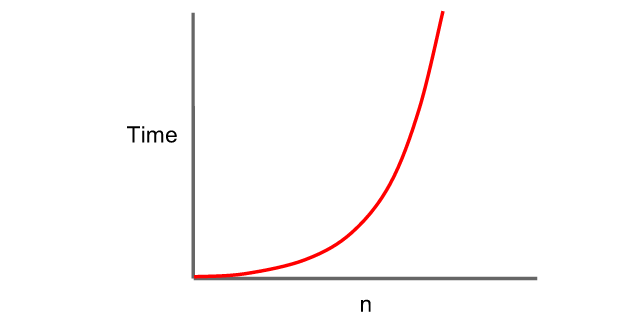
• 중첩 반복문에서 발생하며, 입력값의 2 제곱의 스텝이 필요하다.
• 입력값이 10개라면 10² = 100번의 스텝,
  입력값이 100개이라면 100² = 10,000번의 스텝이 필요하다.

예시)

for(let i = 0; i < n; i += 1) {
  for(let j = 0; j < n; j += 1) {
    // ...
  }
}

O(n²)의 시간복잡도를 가지는 알고리즘

• 선택 정렬(Selection Sort)
• 버블 정렬(Bubble Sort)
• 삽입 정렬(Insertion Sort)

---

O(2ⁿ)

지수 시간(exponential time)
: 입력값(n)이 증가함에 따라, 실행 시간이 두 배씩 증가한다.

• 기하급수적 시간복잡도라고 불리며, Big-O 표기법 중 가장 느린 시간복잡도를 가진다.
• 입력값이 10개라면 2¹⁰ = 1024번의 스텝,
  입력값이 100개라면 2¹⁰⁰ = 126,7650,6002,2822,9401,4967,0320,5376번의 스텝이 필요하다.

예시) 재귀로 구현한 피보나치 수열

function fibo(n) {
  if(n <= 1) return num;
  
  return fibo(n - 1) + fibo(n - 2);
}
// fibo(n)을 호출하면 fibo(n-1)과 fibo(n-2)가 호출되며, 이 호출 작업은 총 n번 반복된다.

O(2ⁿ)의 시간복잡도를 가지는 알고리즘

• 재귀로 구현한 피보나치 수열

❔ 학습 후 궁금한 점

• 병합, 힙, 퀵, 선택, 버블, 삽입 정렬 등 정렬 알고리즘 공부하고 정리하기
• 점근적 표기법의 종류에는 Big-O 표기법 외에도, Θ 표기법, Ω 표기법이 있다.

이 글은 아래 링크를 참고하여 작성한 글입니다.
[알고리즘] Time Complexity (시간 복잡도)
https://www.youtube.com/watch?v=tTFoClBZutw&t=856s