문제

n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다. 가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.

노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 edge가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.

제한사항

노드의 개수 n은 2 이상 20,000 이하입니다.
간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.

입출력 예

입출력 예 설명

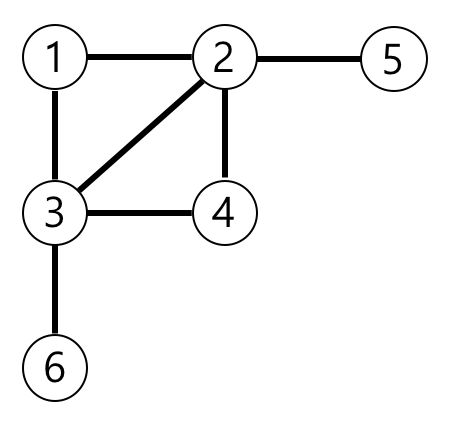
예제의 그래프를 표현하면 아래 그림과 같고, 1번 노드에서 가장 멀리 떨어진 노드는 4,5,6번 노드입니다.

풀이

배열을 queue로 이용한 풀이

function solution(n, edge) {
  const graph = Array.from(Array(n + 1), () => []); 
  // 인접 리스트로 그래프를 만든다. (7) [[], [], [], [], [], [], []] // ❗️이때 fill([])을 이용하면 서로 동일한 참조값을 가진 배열이 7개 만들어지므로, Array.from을 사용해야 한다.
  // index를 n번 정점으로 맞추기 위해 +1 해준다.
  
  for (const [src, dest] of edge) { // 출발지 src, 도착지 dest
    graph[src].push(dest);
    graph[dest].push(src); // 양방향으로 간선을 연결해준다.
  }
  // graph = [[], [3, 2], [3, 1, 4, 5], [6, 4, 2, 1], [3, 2], [2], [3]]
  //              1번 정점       2번           3번         4번    5번  6번
  
  // 1번 정점으로부터 각 정점으로의 거리를 저장할 distance 배열
  const distance = Array(n + 1).fill(0); // [0, 0, 0, 0, 0, 0, 0]
  distance[1] = 1; // 정점 1에서 1까지의 거리는 1이므로 => [0, 1, 0, 0, 0, 0, 0]
  
  // BFS - 가까이 있는 정점부터 탐색
  const queue = [1]; // 배열 queue를 이용해 BFS를 구현한다.
  while (queue.length > 0) { // 빈 큐가 될 때까지 반복한다.
    const src = queue.shift(); // 큐의 맨 앞에서 빼낸 요소            | src = 1                                            | src = 3
    for (const dest of graph[src]) {  // const dest of graph[1] | dest = 3 of graph[1]    | dest = 2 of graph[1]     |  dest = 6 of graph[3]
      if (distance[dest] === 0) { // 방문한 적 없는 노드라면 (0이라면) | distance[3] === 0       | distance[2] === 0        | distance[6] === 0
        queue.push(dest);                   // 큐에 추가해주고,     | queue = [3]             | queue = [3, 2]           | queue = [2, 6]
        distance[dest] = distance[src] + 1; // 도착지에 +1 해준다.  | distance[3] = 1 + 1 = 2 | distance[2] = 1 + 1 = 2  | distance[6] = 2 + 1 = 3
      }
    }
  }
  // queue = [3]
  // distance = [0, 1, 2, 2, 3, 3, 3]
  
  const max = Math.max(...distance); // 최대값 뽑아서
  return distance.filter((item) => item === max).length; // 최대값의 개수 구해서 리턴한다.
}

shift()는 시간 복잡도가 O(N)이지만 요소의 개수가 적을 경우, js 엔진에서 최적화를 해주므로 괜찮다.

queue를 직접 구현한 풀이

class Queue {
  constructor() {
    this.queue = [];
    this.front = 0;
    this.rear = 0;
  }
  
  enqueue(value) {
    this.queue[this.rear++] = value; // rear를 1 늘리고 그 자리에 value 할당
  }
  
  dequeue() {
    const value = this.queue[this.front]; // 반환할 값 = 큐 맨 앞의 값
    delete this.queue[this.front]; // 맨 앞의 값 삭제
    this.front += 1; // front가 가리키는 바꿔주기
    return value; // value 반환
  }
  
  isEmpty() {
    return this.front === this.rear;
  }
}

function solution(n, edge) {
    const graph = Array.from(Array(n + 1), () => []);
    
      for (const [src, dest] of edge) {
        graph[src].push(dest);
        graph[dest].push(src);
      }

    const distance = Array(n + 1).fill(0);
    distance[1] = 1;
    
    const queue = new Queue(); // 큐 생성
    queue.enqueue(1);          // 1 넣고 시작
    
    while (!queue.isEmpty()) { // queue가 완전히 빌 때까지 반복한다.
        const src = queue.dequeue(); // 큐에서 빼기
        for (const dest of graph[src]) {
            if (distance[dest] === 0) { 
                distance[dest] = distance[src] + 1;
                queue.enqueue(dest); // 큐에 넣기
            }
        }
    }
    const max = Math.max(...distance);
    return distance.filter((v) => v === max).length;
}

요소가 적다면 shift()를 사용해도 최적화가 되므로 사용해도 되지만, 요소가 많을 경우 직접 queue를 구현해 사용하는 것이 더 빠르다.