플로이드 와샬 알고리즘 (Floyd Warshall)
: 그래프에서 모든 정점 간의 최단 경로를 찾는 데 사용하는 알고리즘
-
2차원 배열을 사용해 모든 정점 쌍 간의 최단 경로를 계산한다.
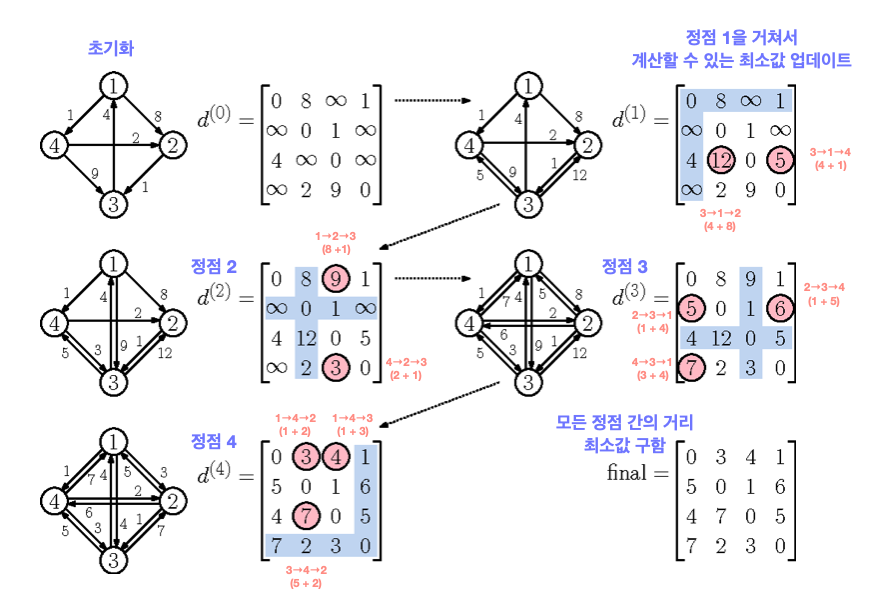
- 초기화 : 모든 정점 간의 거리를
Infinity로 초기화하고, 직접 연결된 간선이 있는 경우에는 해당 간선의 가중치로 설정한다. - 중간 정점을 거쳐가는 경우를 고려하면서, 각 정점 간의 최단 경로를 갱신한다. 이때 중간 정점은 1부터 N까지의 정점 중 하나이다.
- 모든 중간 정점에 대해 위 단계를 반복하여 최단 경로를 업데이트한다.
- 초기화 : 모든 정점 간의 거리를
-
플로이드 와샬 알고리즘은 정점의 수가
V일 때, 모든 정점 간의 최단 경로를 구하는 데O(V³)의 시간 복잡도를 가진다. 따라서 정점의 수가 매우 큰 경우에는 실행 시간이 길어질 수 있다. -
다익스트라 알고리즘이나 벨만-포드 알고리즘과 달리 음(-)의 가중치를 가진 간선을 포함한 그래프에서도 동작한다.
플로이드 와샬 문제 풀이
플로이드
문제 설명
n(2 ≤ n ≤ 100)개의 도시가 있다.
그리고 한 도시에서 출발하여 다른 도시에 도착하는 m(1 ≤ m ≤ 100,000)개의 버스가 있다.
각 버스는 한 번 사용할 때 필요한 비용이 있다.
모든 도시의 쌍 (A, B)에 대해서 도시 A에서 B로 가는데 필요한 비용의 최솟값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다.
그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다.
버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다.
시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있다.
출력
n개의 줄을 출력해야 한다. i번째 줄에 출력하는 j번째 숫자는 도시 i에서 j로 가는데 필요한 최소 비용이다.
만약, i에서 j로 갈 수 없는 경우에는 그 자리에 0을 출력한다.
입출력 예
| 입력값 | 출력값 |
|---|---|
| 5 (n) 14 (m) 1 2 2 1 3 3 1 4 1 1 5 10 2 4 2 3 4 1 3 5 1 4 5 3 3 5 10 3 1 8 1 4 2 5 1 7 3 4 2 5 2 4 | 0 2 3 1 4 12 0 15 2 5 8 5 0 1 1 10 7 13 0 3 7 4 10 6 0 |
문제 풀이
const fs = require('fs');
const filePath = process.platform === 'linux' ? '/dev/stdin' : './input.txt';
const lines = fs.readFileSync(filePath).toString().trim().split('\n');
const numOfCity = parseInt(lines[0]); // 5
const numOfBus = parseInt(lines[1]); // 14
const busCostTable = [];
for (let i = 2; i < lines.length; i++) {
const [from, to, cost] = lines[i].split(' ').map(Number);
busCostTable.push([from, to, cost]); // [ [1, 2, 2], [1, 3, 3], [1, 4, 1], ... [5, 2, 4] ]
}
// 각 도시 → 도시로 이동할 때 필요한 비용 배열 초기화
const graph = Array.from({ length: numOfCity }, (_, i) => Array.from({ length: numOfCity }, (_, j) => (i === j ? 0 : Infinity)));
// [
// [ 0, Infinity, Infinity, Infinity, Infinity ],
// [ Infinity, 0, Infinity, Infinity, Infinity ],
// [ Infinity, Infinity, 0, Infinity, Infinity ],
// [ Infinity, Infinity, Infinity, 0, Infinity ],
// [ Infinity, Infinity, Infinity, Infinity, 0 ]
// ]
for (const [from, to, cost] of busCostTable) {
graph[from - 1][to - 1] = Math.min(graph[from - 1][to - 1], cost);
// 같은 도시에서 같은 도시로 노선이 있을 수 있으므로 이미 존재하는 노선이라면 비용이 적은 값을 업데이트하도록한다.
}
// [
// [ 0, 2, 3, 1, 10 ],
// [ Infinity, 0, Infinity, 2, Infinity ],
// [ 8, Infinity, 0, 1, 1 ],
// [ Infinity, Infinity, Infinity, 0, 3 ],
// [ 7, 4, Infinity, Infinity, 0 ]
// ]
// 위에서 만든 graph를 순회하며 최솟값을 업데이트한다.
for (let mid = 0; mid < numOfCity; mid++) { // 거쳐가는 도시
for (let from = 0; from < numOfCity; from++) { // 출발 도시
for (let to = 0; to < numOfCity; to++) { // 도착 도시
if (graph[from][mid] + graph[mid][to] < graph[from][to]) { // 만약 mid 도시를 거쳐가는 비용이 from 도시서 to 도시로 바로 가는 것보다 비용이 낮다면
graph[from][to] = graph[from][mid] + graph[mid][to]; // 해당 값으로 업데이트한다.
}
}
}
}
// 만약 Infinity값이 남아있다면 해당 도시에서 도시로 가는 노선이 없다는 뜻이므로 0으로 바꾸어준다.
for (let i = 0; i < numOfCity; i++) {
for (let j = 0; j < numOfCity; j++) {
if (graph[i][j] === Infinity) graph[i][j] = 0;
}
}
graph.forEach((arr) => {
console.log(arr.join(' '));
});순위
문제 설명
n명의 권투선수가 권투 대회에 참여했고 각각 1번부터 n번까지 번호를 받았습니다.
권투 경기는 1대1 방식으로 진행이 되고, 만약 A 선수가 B 선수보다 실력이 좋다면 A 선수는 B 선수를 항상 이깁니다.
심판은 주어진 경기 결과를 가지고 선수들의 순위를 매기려 합니다. 하지만 몇몇 경기 결과를 분실하여 정확하게 순위를 매길 수 없습니다.
선수의 수 n, 경기 결과를 담은 2차원 배열 results가 매개변수로 주어질 때 정확하게 순위를 매길 수 있는 선수의 수를 return 하도록 solution 함수를 작성해주세요.
제한사항
선수의 수는 1명 이상 100명 이하입니다.
경기 결과는 1개 이상 4,500개 이하입니다.
results 배열 각 행 [A, B]는 A 선수가 B 선수를 이겼다는 의미입니다.
모든 경기 결과에는 모순이 없습니다.
입출력 예
| n | results | return |
|---|---|---|
| 5 | [[4, 3], [4, 2], [3, 2], [1, 2], [2, 5]] | 2 |
입출력 예 설명
2번 선수는 [1, 3, 4] 선수에게 패배했고 5번 선수에게 승리했기 때문에 4위입니다.
5번 선수는 4위인 2번 선수에게 패배했기 때문에 5위입니다.
문제 풀이
function solution(n, results) {
// 각 선수간의 승패를 저장할 배열, 나 자신은 0, 경기한 적 없다면 false로 초기화
const graph = Array.from({length : n}, (_, i) => Array.from({length : n}, (_, j) => i === j ? 0 : false));
// [
// [ 0, false, false, false, false ],
// [ false, 0, false, false, false ],
// [ false, false, 0, false, false ],
// [ false, false, false, 0, false ],
// [ false, false, false, false, 0 ]
// ]
// results 배열을 순회하며 내가 이긴 상대에게는 1, 내가 진 상대에게는 -1을 저장한다.
results.forEach(([winner, loser]) => {
graph[winner - 1][loser - 1] = 1;
graph[loser - 1][winner - 1] = -1;
});
// [
// [ 0, 1, false, false, false ],
// [ -1, 0, -1, -1, 1 ],
// [ false, 1, 0, -1, false ],
// [ false, 1, 1, 0, false ],
// [ false, -1, false, false, 0 ]
// ]
for (let mid = 0; mid < n; mid++) {
for (let a = 0; a < n; a++) {
for (let b = 0; b < n; b++) {
// a가 mid를 이기고, mid가 b를 이기면 a가 b를 이김
if (graph[a][mid] === 1 && graph[mid][b] === 1) {
graph[a][b] = 1;
}
// a가 mid에게 지고, mid가 b에게 지면 a가 b에게 짐
if (graph[a][mid] === -1 && graph[mid][b] === -1) {
graph[a][b] = -1;
}
}
}
}
// [
// [ 0, 1, false, false, 1 ],
// [ -1, 0, -1, -1, 1 ], -> 순위 알 수 있음
// [ false, 1, 0, -1, 1 ],
// [ false, 1, 1, 0, 1 ],
// [ -1, -1, -1, -1, 0 ] -> 순위 알 수 있음
// ]
let answer = 0;
graph.forEach((player) => {
if (player.includes(false)) return; // 배열에 false 값을 가진 선수는 정확한 순위를 알 수 없으므로 answer에 추가하지 않는다.
answer++;
});
return answer;
}


이건 처음 들어보는 알고리즘 개념이네요…!
고생하셨습니다