[백준]9063 - 대지

| 문제
임씨는 1950 년 한국전쟁으로 많은 손해를 본 사람들 중 하나다. 전쟁 통에 손해보지 않은 사람이 어디 있을까 만은 그는 6.25 가 일어나기 전만 해도 충청도 지방에 넓은 대지를 소유한 큰 부자였다. 전쟁이 나자 임씨는 땅문서와 값 나가는 것들만 챙겨서 일본으로 피난을 가지만 피난 중에 그만 땅문서를 잃어버리고 만다. 전쟁이 끝난 후에 임씨의 땅은 이미 다른 사람들의 논밭이 되어 있었고, 임씨는 땅을 되찾으려 했지만 문서가 없으니 생떼 쓰는 것과 다를 바 없었다. 이러다가 임씨는 길바닥에 나앉게 생겼다.

이때, 임씨에게 좋은 생각이 떠올랐으니 바로 자신이 습관처럼 땅 깊숙이 뭔가 표식을 해놓았던 사실이다. 임씨는 한적할 때마다 자신의 논밭을 거닐다가 땅속 깊은 곳에 자신의 이름이 씌어진 옥구슬을 묻어놓았던 것이다. 즉, 어떤 지점에서 그의 이름이 적힌 옥구슬이 나온다면 그 지점은 예전에 임씨의 땅이었다는 것을 증명하는 것이다.

임씨는 즉시 민사소송을 통해 자신의 땅을 찾고자 했고 논리적인 근거를 들어 옥구슬이 나오는 지점이 원래 자신의 땅의 한 지점이었다는 것을 주장하여 결국 담당판사를 설득하는 데에 성공하였다. 담당판사는 다음과 같은 판결을 내렸다. “ 6.25 이전의 개인소유 대지들은 99%가 남북, 동서 방향으로 평행한 직사각형 모양이었으므로, 임씨의 이름이 새겨진 옥구슬이 나오는 모든 지점을 포함하는 가장 작은 남북, 동서 방향으로 평행한 변을 갖는 직사각형의 대지를 임씨의 소유로 인정한다.” 임씨는 많은 손해를 보는 셈이지만 더 이상을 요구할 만한 근거가 없었기 때문에 이 판결을 따르기로 했다.

임씨의 이름이 새겨진 옥구슬의 위치 N 개가 주어질 때에, 임씨에게 돌아갈 대지의 넓이를 계산하는 프로그램을 작성하시오. 단, 옥구슬의 위치는 2 차원 정수 좌표로 주어지고 옥구슬은 같은 위치에 여러 개가 발견될 수도 있으며, x 축의 양의방향을 동쪽, y 축의 양의방향을 북쪽이라고 가정한다.

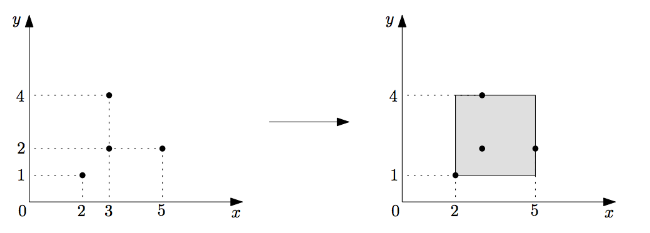
예를 들어 위와 같이 (2, 1), (3, 2), (5, 2), (3, 4) 네 점에서 옥구슬을 발견하였다면, 임씨에게 돌아갈 대지는 (2, 1), (5, 1), (2, 4), (5, 4)를 네 꼭짓점으로 하는 직사각형이며, 넓이는 (5 - 2) × (4 - 1) = 9 가 된다.

| 입력
첫째 줄에는 점의 개수 N (1 ≤ N ≤ 100,000) 이 주어진다. 이어지는 N 줄에는 각 점의 좌표가 두 개의 정수로 한 줄에 하나씩 주어진다. 각각의 좌표는 -10,000 이상 10,000 이하의 정수이다.

| 출력
첫째 줄에 N 개의 점을 둘러싸는 최소 크기의 직사각형의 넓이를 출력하시오.

| 예제 입력1
3
20 24
40 21
10 12

| 예제 출력1
360

| 예제 입력2
1
15 13

| 예제 출력2
0

| 예제 입력3
4
2 1
3 2
5 2
3 4

| 예제 출력3
9

package BaekJoon;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class A9063 {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));

		try {
	
			int N=Integer.parseInt(bf.readLine()); //점의 갯수
			
			int minCompareX=Integer.MAX_VALUE;//x 최솟값 비교를 위해 integer.max_value 선언
			int maxCompareX=Integer.MIN_VALUE; //x 최댓값 비교를 위해 integer.min_value 선언
			int minCompareY=Integer.MAX_VALUE; //y 최솟값 비교를 위해 integer.max_value 선언
			int maxCompareY=Integer.MIN_VALUE; //y 최댓값 비교를 위해 integer.min_value 선언
			
			for(int i=0;i<N;i++) {
				StringTokenizer st=new StringTokenizer(bf.readLine());
				
				int x=Integer.parseInt(st.nextToken());
				int y=Integer.parseInt(st.nextToken());
				
				//값이 들어오는 것에 따라 최소 최대 비교
				//math.min(a,b) : a와 b를 비교하여 최솟값 , math.max(a,b) : a와 b를 비교하여 최댓값 출력
				minCompareX=Math.min(minCompareX, x);
				maxCompareX=Math.max(maxCompareX, x);
				minCompareY=Math.min(minCompareY, y);
				maxCompareY=Math.max(maxCompareY, y);
				
				
			}
			int extent=(maxCompareX-minCompareX)*(maxCompareY-minCompareY);
			System.out.println(extent);
			
		} catch (IOException e) {
			// TODO Auto-generated catch block
			e.printStackTrace();
		}
		
	}

}

---

| 느낀점
문제 해석을 하면 결국 (X축의 최댓값-X축의 최솟값)*(Y축의 최댓값-Y축의 최솟값)=넓이 즉, 넓이를 구하는 문제였다.
최소, 최댓값을 구하는 과정에서 int min=Integer.MAX_VALUE를 / int max=Integer.Min_VALUE를 구하는 부분이 이해가 안갔다.
최솟값 비교를 하는데 왜 MAX_VALUE 최댓값으로 값을 초기화 하고,
최댓값 비교를 하는데 왜 MIN_VALUE 최솟값으로 값을 초기화 하는지가 이해함에 있어 어렵게 느껴졌다.(생각해보면 바보였던 듯)

for문에서 Math.min(a,b) 메서드를 이용해 결국 두 값을 비교해 더 최솟값 / Math.max(a,b) 최댓값을 구해야 되는데, 위에서 int min을 최솟값으로 아예 초기화 하고 시작하면 그 값이 최소이기 때문에 for문을 돌면서 최소, 최대를 비교할 수 없다는 것을 풀면서 이해했다.

Math클래스는 사용하기 용이한 많은 메서드들이 있는 것 같다.
해당 부분도 포스팅하도록 하자!