1. (경) 첫 포스팅 (축) 😃
이전에 쓰던 블로그가 맘에 안들어서 최근 velog 에 관한 포스팅을 보고 새롭게 넘어왔다.
심플하면서도 보기좋은 디자인은 갖춰놓은 느낌에, 다른 블로거들도 거의 통일된 스타일의 블로그를 운영하는 모습이 참 좋았던 것 같다.
필자의 미적감각은 0에 수렴하기 때문에 다른 블로거들의 블로그들을 들어가면 뭔가 내 꺼는 2프로 부족한 느낌이 늘 있었는데, 여기에선 안 그(럴것이다)렇다. 편-안 하다.
다만 한 가지 아쉬운 점은 카테고리가 1차원적이라는 것이다. IT-자료구조-스택 이런식으로 범주가 세분화 되어있지 않고, IT , 자료구조, 스택 이 각각 동등한(?) 부분처럼 보인다.
물론 배부른 소리다. 블로그 다시 시작해야지라는 다짐이 한달을 넘은 지금, 찬밥을 가릴 때가 아니련만.. velog가 아무쪼록 내 새로운 이야기를 풀어나가는 좋은 발판이 되어주었으면 좋겠다.
2. 어떤걸 다룰 것인가?
자료구조에 관한 블로그 글은 수도 없이 많다. 그러나 필자는 수업 때 어렵다고 느낀 것들, 또는 심화적이었다고 생각하는 것만을 예시를 통해 이 시리즈에서 다룰 예정이다. 이론으로 잘 이해했다고 느껴도 예제를 해결하지 못할 때가 잦았기 때문이다. 물론 이는 주관적인 요소라 때로는 매우 기본적인 개념임에도 본인의 몰이해에서 비롯된 사례가 있음을 감안해주길 바란다.
추가로 이 글은 기초적인 프로그래밍 경험, 자료구조에 대한 맛보기가 선행되어 있는 분들에게 유익할 것이라 기대한다.
이해하기 어려웠던 개념 or 심화 개념 + 실전 문제 풀이
3. 성능 분석 : 공간복잡도 / 시간복잡도
전자는 메모리 사용량에 대한 분석 결과, 후자는 수행시간 분석 결과를 나타낸다.
가장 기본임에도 불구하고 한번 놓치니 계속 헷갈렸던 개념이다.
- 공간복잡도
int test1(int a)
{
return a * a;
}위 함수의 공간 복잡도는? 물론 n*n이다.
(교수님 : 뭣이?)
라고 생각한게 코린이 시절의 나였다.
기억하자. 모든 성능은 알고리즘에 관한 것이다. 코드를 돌리기 위한 시스템에 대한 고려는 필요가 없으며, 값 또한 신경쓰지 않는다. 그렇다면 위 문제의 답은? 0이다. 어떠한 할당도 없이 파라미터가 바로 리턴 되었기 때문이다.
만약 int b = a * a; 를 했다면 공간복잡도는 1이 됐을 것이다.
int test2(int arr[], int n) {
int result = 0;
for (int i = 0; i < n; i++) {
result = result + arr[i];
}
return result;
}이 문제는 어떨까? 변수들을 파악하는게 우선이다. 변수는 arr[], n, result, i 가 있다.
이 알고리즘은 arr 배열에 대한 n개의 변수가 저장되고 있고, i, n, result는 모두 for문 내에서 연산을 위해 활용되고 있다. 즉 이 알고리즘에서는 n + 3 의 공간복잡도를 보여준다.
int test3(int arr[], int n) {
if (n == 0)
return 0;
else
return (test3(arr, n - 1) + arr[n]);
}이 문제는 재귀함수가 들어가서 더 귀찮다. 나 같은 초보는 이런 코드를 보면 스턴을 먹으니 값을 대입해 봐야겠다.
arr[5] = {1, 2, 3, 4, 5} 으로 가정 ------> sum(arr, 3) 실행 ------> return 값은?
sum(2) + arr[3] -> sum(1) + arr[2] -> sum(0) + arr[1] 에서 sum(0) =0 이니까
0 + 2 + 3 + 4 = 9 가 되시겠다. 여기서 1이 아니라 0인 이유는 잘 아시리라 생각한다.
이 알고리즘은 test2 에서 본 for문 처럼 반복 수행을 하지만 원래 함수로 돌아오는 기능을 수행하고 있다.
즉, 원 함수로 복귀하는 주소가 할당되어야 한다는 것이다. 즉 일반적인 sum 함수는 3개의 공간이 필요하다.
필요 공간 : arr, n , 복귀용 주소
또한 3을 대입했을 경우 위에서 본대로 2회의 call 이 이뤄진다. (화살표 개수) 이를 일반화 하면 n-1번의 수행이 이뤄지는 것으로 이해할 수 있다.
물론 엄밀히 말하면 sum(0)에서도 call 이 이뤄지지만 if(n==0) return 0; 만을 수행하는 알고리즘은 test1와 동일하게 무의미한 경우에 해당되므로 제외한다.
결과적으로 'call 의 횟수 * 필요 공간 = 공간복잡도' 가 된다. 즉, (n-1) x 3이다.
- 시간복잡도
코린이 : '아 이제 난 공간복잡도를 마스터 했어!'
아쉽게도 성능분석 측면에서 공간복잡도는 시간복잡도에 비해 영 ~뒷전인게 사실이다.
다음 예시를 살펴보자.
void test1(int n) {
int a, i;
for (i = 0; i < n; i++)
a = i;
}코린이 : 이건 쉽네~ i가 0 부터 n 미만 까지 증가하면 총 n번 실행되는 셈이니 -> a=i 가 n번 실행되니 답은...
단순함에 속을뻔했군 i++ 는 i=i+1 과 같은말이 아니던가? 그렇다면 답은 n + n = 2n 이다!
저 함정에 필자는 걸려들었던 기억이 있다. 그렇다면 코린이의 답은 맞았을까? 현실적으로는 2n 으로 봐도 문제가 없을 테지만 엄밀한 계산으로는 2n + 1 이 맞다.
간단하게 n =3 이라 가정하면 i가 0 -> 1 -> 2 -> 3 을 거치다가 3이되면 3 < n 이 성립하지 않음을 확인하고 for문이 종료된다. 즉 4번의 검문이 이뤄지는 것이다.
이는 사실 현실적인(n이 매우 큰 수가 될 때) 시간복잡도의 고려 범위를 벗어난 것으로 big-O를 통해 최고차항만 남기면 2n이나 2n+1 이나 O(n) 이 된다.
test1에서 i++ 를 i=i+2 로 바꾸면? n까지 가는 도달 속도가 2배로 느니 n+1 은 2n+1 이 되고, n은 n/2가 될 것이다.
그 외에도 n 을 n*n 으로 바꾸는 등의 응용이 가능하다.
void test2(int n) {
int a, i, j;
for (i=0;i<n;i++) // n+1
for (j=0;j<i;j++) // (i=0 일떄 +1) + (i=1일 때 +1) + .. (i=n-1일때 + 1)
a=i; // 즉, 1 + 2 + 3 + .. + n = n(n+1)/2 이다
} // a=i 는 총 n(n+1)/2 -1 만큼 시행될 것이다. test2 의 각 값들을 모두 더하면 n(n+2) 가 나온다. 이는 O(n^2) 으로 표현할 수 있겠다.
4. Matrix
매트릭스는 이산수학에서, 또는 2차원 배열을 통해 자주 접할 수 있는 개념이다.
그런데 그림으로 그려서 지우거나 쓰면 편하게 생각할 수 있지만 이를 프로그래밍으로 구현하는 상당히 까다로운 문제다.
- Transposing Matrix
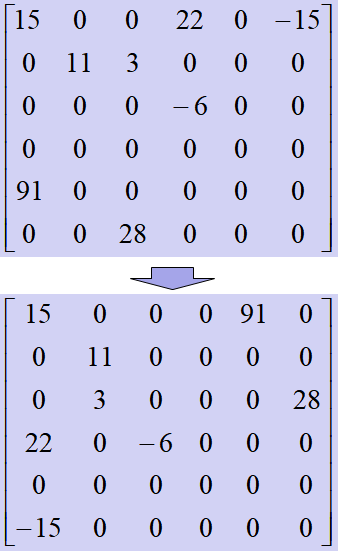
위 그림은 행과 열이 서로 바뀌는 모습을 보여준다. 처음 접하는 사람들에게는 이를 구현하는게 어렵게 느껴지지 않는다. 코린이 시절엔 그냥
temp = row[a];
row[a] = col[MAX-a];
col[MAX-a] = temp;이거만 반복하면 되겠지? 라고 생각 했다. (사실 이 방식으로 해결하는게 맞긴 하다) 그렇게 작성된 코드가 바로 아래와 같다.
int M[6][6] = { {15, 0, 0 ,22, 0, -15 }
, {0, 11, 3, 0, 0, 0 }
, {0, 0, 0, -6, 0,0 }
, {0, 0, 0, 0, 0, 0 }
, {91, 0, 0, 0, 0, 0 }
, {0, 0, 28, 0, 0 ,0 } };
int temp[6][6];
for (int i = 0; i < 6; i++)
for (int j = 0; j < 6; j++)
temp[i][j] = M[i][j]; //temp 에 M을 복사
for (int i = 0; i < 6; i++)
for (int j = 0; j < 6; j++)
M[i][j] = temp[j][i]; //역순으로 M에 temp를 붙여넣기
이후 M을 출력하면 깔끔하게 transpose된 행렬이 나온다. 코드도, 결과도 만족스럽다.
(그냥 역순으로 저장한게 다다)
그런데 수업 때는 이런 개념을 배운다.
- Fast Matrix Transposing
코린이 : 아니 이게 뭐람?
사실 n 이 6 정도 되는 행렬이면 필자는 위 방식으로 하는게 맞다고 생각한다. 얼마나 직관적이고 간단한가? 그러나 현실에서 마주하게 될 것들은 아주 큰 수일 것이다. 그 많은 수를 모두 복사하고 붙여넣는 것은 앞서 배운 성능 효율이 아주 떨어지는 상황인 것이다. (특히 0이 많은 경우 그렇다) 좀 더 Fast한 상황이 필요하다.
Fast 한 Transposing 을 위해 우리는 다음 두 조건이 필요하다.
value가 0이 아닌 행렬표, rowterms (startingpos 를 만들기 위한 표) , startingpos (바뀌는 위치)
행렬표는 아래와 같이 제시될 수 있다. 즉 0들이 많은 2차원 배열로 몽땅 담을 생각부터가 틀렸다.
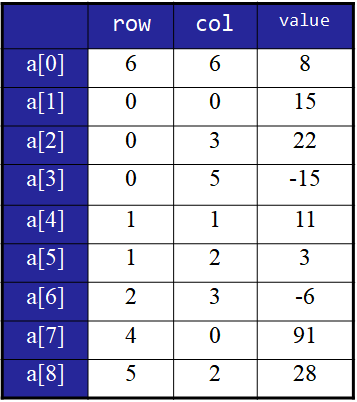(참고로 a[0] 의 값은 상징적인 값이다. 행이 6개, 열이 6개 있고 0이 아닌 값은 8개 있음을 명시해준 것이다)
이 초기설정은
typedef struct M {
int row;
int col;
int value;
}m;처럼 구조체를 기반으로
m a[9]; //원본
a[0].row = 6; a[0].col = 6; a[0].value = 8;
a[1].row = 0; a[1].col = 0; a[1].value = 15;
a[2].row = 0; a[2].col = 3; a[2].value = 22;
a[3].row = 0; a[3].col = 5; a[3].value = -15;
a[4].row = 1; a[4].col = 1; a[4].value = 11;
a[5].row = 1; a[5].col = 2; a[5].value = 3;
a[6].row = 2; a[6].col = 3; a[6].value = -6;
a[7].row = 4; a[7].col = 0; a[7].value = 91;
a[8].row = 5; a[8].col = 2; a[8].value = 28;
m b[9]; //붙여넣을 것
int rowterms[6] = {0, };
int startingpos[6] = {0, };(..)이렇게 표현할 수 있다.
여기서 rowterms는 a의 column 값들의 개수를 나타내고 startingpos는 rowterms와
startingpos[0] = 1; startingpos[n] = rowterms[n-1] + startingpos[n-1];
의 관계를 갖고 있다. 이를 코드로 나타내면,
for (int i = 1; i <= a[0].value; i++)
rowterms[a[i].col]++;
startingpos[0] = 1;
for (int i = 1; i < MAX; i++)
startingpos[i] = rowterms[i-1] + startingpos[i-1];이 된다. 그럼 이 startingpos는 어떻게 위치를 나타내는 역할을 하는 걸까?
b의 index 는 a의 i번째 열을 index로 한 startingpos의 값이다.
즉, b_index = startingpos[a[i].col] ++ // 이후 startingpos의 해당 값은 증가한다.
코린이들은 여기부터 스턴을 먹는다. 나도 그냥 외웠었다.
이는 rowterms의 존재의미와 같이 생각해야 이해가 되는 것 같다.
startingpos는 rowterms를 이용해 a행렬의 열이 1인경우 ~ n인 경우들 각각의 시작위치를 부여한다.
즉, a의 특정 열을 넣으면 바로 그곳에 대응될 b의 행, 열, 값의 위치를 제공하는 것이 startingpos인 것이다.
이후에는 index에 해당하는 열과 행을 바꿔서 대입하면 끝난다.
int b_index = 0;
for (int i = 1; i <= a[0].value; i++) {
b_index = startingpos[a[i].col]++;
b[b_index].row = a[i].col;
b[b_index].col = a[i].row;
b[b_index].value = a[i].value;
}결과는 다음과 같이 나타날 것이다.
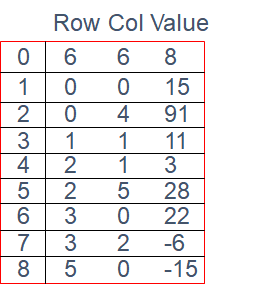
다음 포스팅에서는 union, stack, queue에 관해 알아보자.
