• 문제: https://www.acmicpc.net/problem/2805

설명

이 문제를 풀 때 계속 실수한 점은 M 미터의 나무를 잘랐다고 반복을 멈췄다는 것이다.
문제를 읽어보면 이때, **적어도 M미터**의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 **높이의 최댓값**을 구하는 프로그램을 작성하시오. 적어도 M미터, 높이의 최댓값에서 최적값이 따로 있을 수 있기 때문이다.

여기서 최소한 M미터를 챙겨가는 절단기의 최대 높이 K를 구한다는 최적화 문제는 '결정 문제'로 바꾸어 풀 수 있다. 이것을 파라메트릭 서치라고 한다.

• 자세한 내용 참고: https://sarah950716.tistory.com/16

즉 우리는 나무의 높이 배열이 주어졌을 때, 절단기의 높이가 x인 경우 잘린 나무들의 길이 합이 M미터 이상인가 확인하고 이때 x의 최댓값을 구한다.

방법은 다음과 같다.
나무 높이 배열이 [20, 15, 10, 17]일 때, 탐색을 통해 15라는 값을 구했지만 그 값이 최적이 아닐 수도 있다.

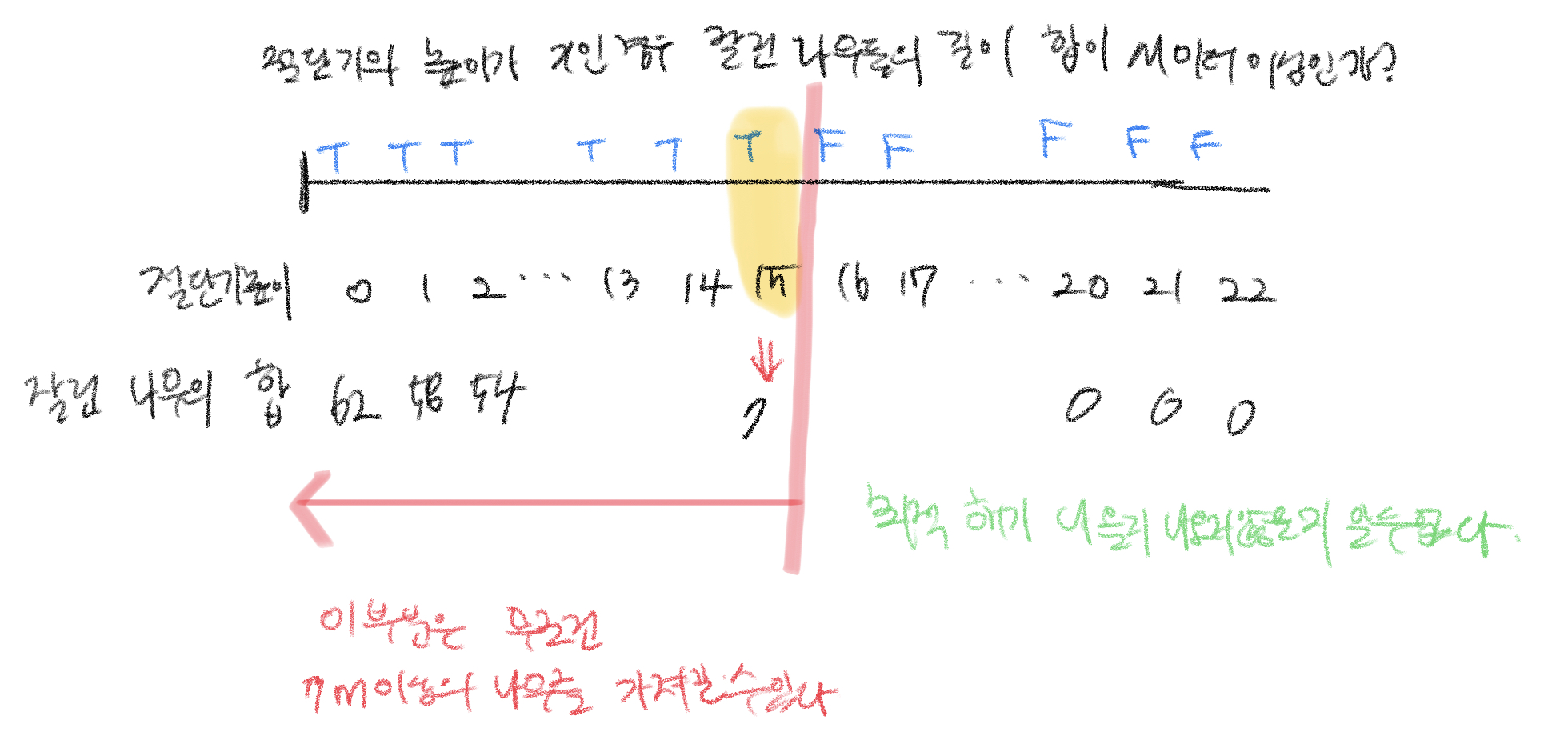
결국 반복을 하다가 종료된 시점에 오른쪽 원소가 가리키는 값이 최대값이 된다.
이 문제에서는 해당 지점이 정답인지, 아닌지 판단하는 방법은 다음과 같다.

def buyTree(tree, target):
    while(left <= right):
        total = 0
        middle = (left + right) // 2
		
        # 1. 해당 높이에서 나오는 넓이의 합을 구한다.
        for height in tree:
            if (height - middle) >= 0:
                total += (height - middle)

            if total > target:
                break

		# 2. 합과 목표치를 비교한다.
        if total < target:
            right = middle - 1
        elif total >= target:
            left = middle + 1
	result = right

결정해야하는 구간이 이 문제처럼 T~F가 아닌 F~T 일수도 있다. 따라서 문제에 따라 정답을 잘 반환하는 것이 필요하다.

코드

N, M = map(int, s.readline().split())

tree = list(map(int, s.readline().split()))
result = 0

def buyTree(tree, target):
    global result
    left, right = 1, max(tree)

    while(left <= right):
        total = 0
        middle = (left + right) // 2

        for height in tree:
            if (height - middle) >= 0:
                total += (height - middle)

            if total > target:
                break

        if total < target:
            right = middle - 1
        elif total >= target:
            left = middle + 1
	result = right

buyTree(tree, M)
print(result)

Reference

• https://velog.io/@jxlhe46/%EB%B0%B1%EC%A4%80-2805%EB%B2%88.-%EB%82%98%EB%AC%B4-%EC%9E%90%EB%A5%B4%EA%B8%B0