설명
이 문제 풀이 방법은 크게 분할 정복과 스택 자료 구조를 사용하는 방식이 있다.
개인적인 감상으로는 분할 정복은 머지 정렬이 떠올랐고, 스택은 앞에서 풀이한 탑 문제가 떠올랐다.
분할 정복 방식
일단 문제의 목표는 가장 넓이가 큰 직사각형을 구하는 것이다. 각 사각형의 너비가 모두 1이기 때문에 1) 높이는 길고 2) 너비는 넓게 직사각형을 그리자.
머지 정렬처럼 가장 작은 단위(너비가 1)까지 히스토그램을 나눈 후에 좌우를 비교하면서 넓이가 큰 직사각형을 구한다.
그렇다면 풀이 과정은 크게 다음과 같다.
- 가운데 위치를 구한다. (
mid = low + high // 2) - 가운데 위치를 기준으로 좌, 우 너비를 각각 구한다.
- 좌, 우 너비 중 최대 너비를 구한다.
- mid를 포함하여 너비를 구한 것(좌, 우 구간을 합침)과 좌,우 너비 중 최대 너비 중 큰 것을 결정한다.
def getArea(low, high):
# 막대 폭(넓이)이 1이면, 높이가 넓이가 된다.
if low == high:
return histogram[low]
# 1. 가운데 위치를 구한다.
mid = (low + high) // 2
# 2. 가운데 위치 기준으로 나눠서 재귀적으로 넓이를 구한다.
leftArea = getArea(low, mid)
rightArea = getArea(mid+1, high)
# 3. leftArea와 rightArea 중 큰 것을 구한다.
maxArea = max(leftArea, rightArea)
# 4. 구간의 최대 넓이를 구한다.
maxArea = max(getMidArea(low, high, mid), maxArea)
return maxArea그럼 4번째 단계에서 mid를 포함한 넓이는 어떻게 구할까?
일단 합치는 단계에서 좌, 우 구간은 각자의 최대 넓이를 구한 상태이다. 이번에는 mid를 기준으로 양쪽으로 나가면서 두 구간 사이의 겹친 넓이를 탐색한다.
이때! 우리의 방향성은 높이는 높게, 넓이는 넓게를 기억하고 이동한다.
예시의 히스토그램을 가지고 가운데 넓이를 구하겠다.
1. 처음과 끝 인덱스를 2로 나눈 몫인 mid값이 가리키는 값은 높이 5이다. 너비가 1이므로 maxArea = 5, height = 5가 된다.
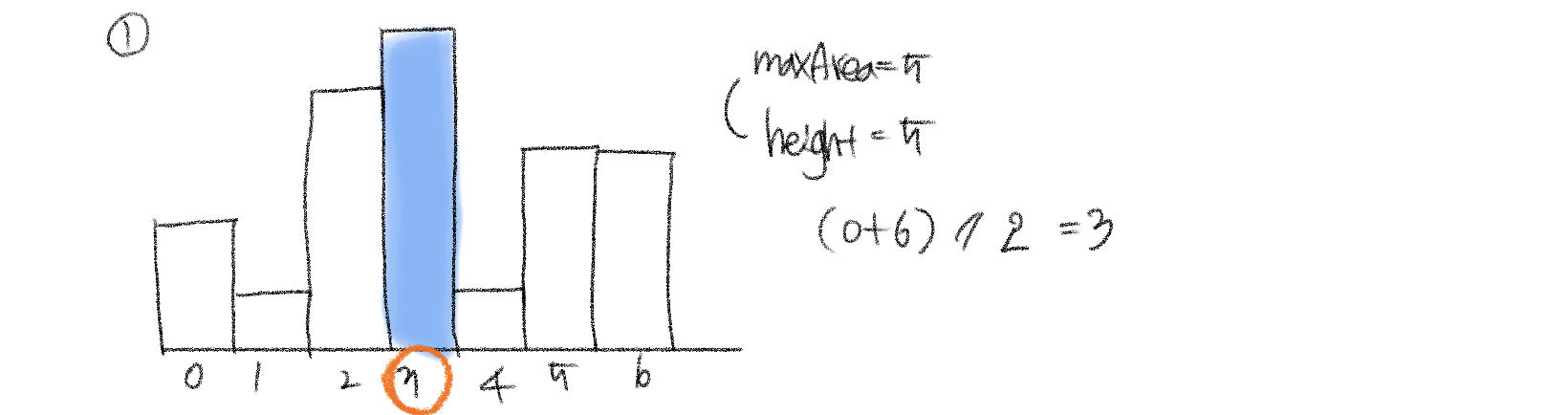
2. mid를 기준으로 왼쪽으로 바라볼지, 오른쪽을 바라볼지 선택한다. 우리의 목표는 넓이를 크~게 만드는 것이기 때문에 height가 높은 인덱스 2가 있는 왼쪽 방향으로 이동한다.
이동하면 maxArea는 2*4 = 8이고, height는 높이를 낮은 쪽으로 갱신하여 4가 된다. 만약 높이를 그대로 5로 가져간다면 올바른 넓이값을 구할 수 없다.
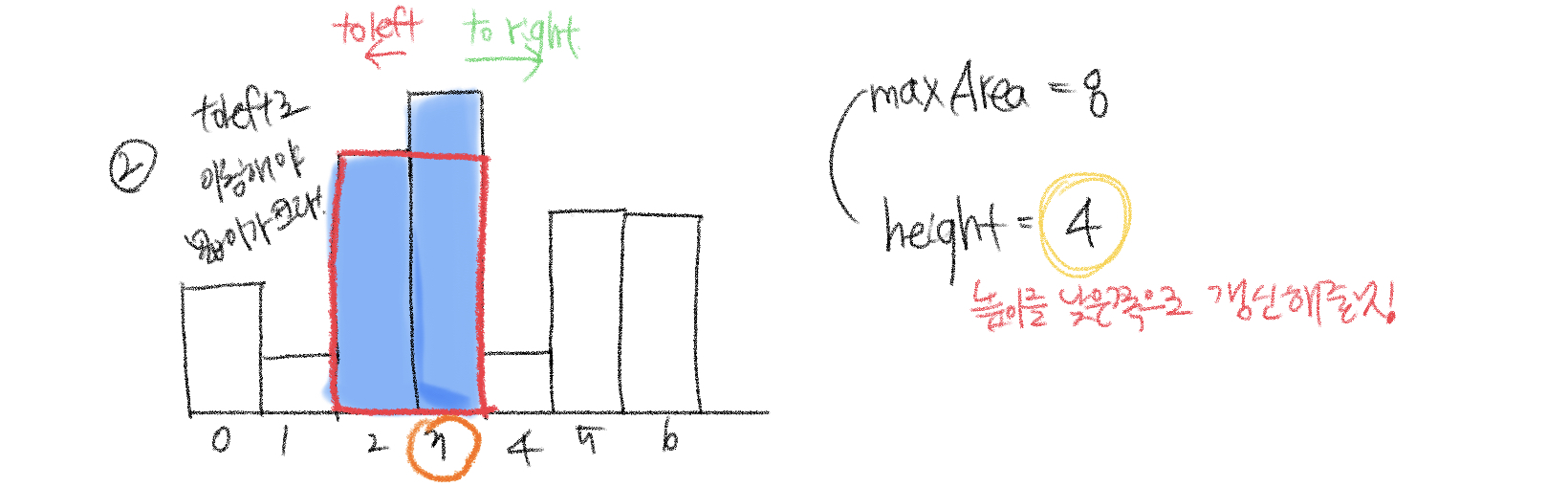
3. 방향을 설정하여 추가로 탐색한다. height는 갱신되고, maxArea는 새로 만들어진 넓이가 8보다 크지 않기 때문에 바뀌지 않는다.
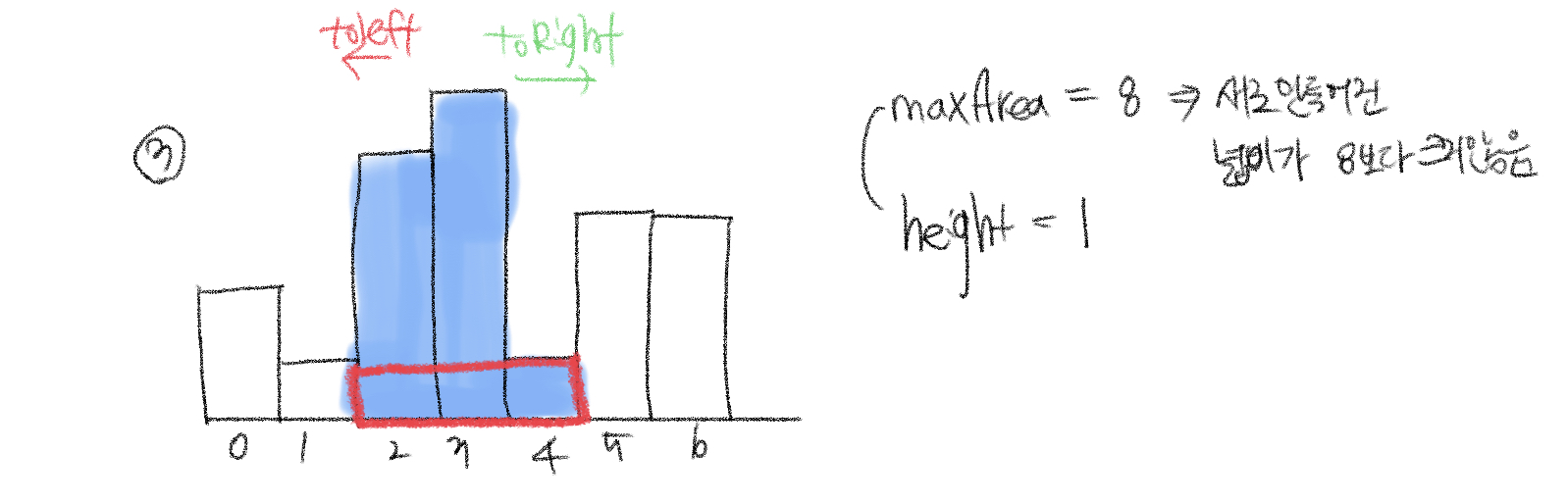
이런식으로 좌, 우를 계속 탐색해 나가면 된다.
만약 한쪽이 먼저 탐색이 끝났다면, 아직 탐색이 완료되지 않은 방향으로 이동하여 탐색을 마무리한다.
def getMidArea(low, high, mid):
toLeft = mid
toRight = mid
height = histogram[mid] # 높이를 구한다.
maxArea = height # 폭이 1이므로 넓이가 높이, 즉 면적이 된다.
# toLeft: 왼쪽으로 이동 -> 탐색 범위 중 가장 낮은 값인 low보다 크다.
# toRight: 오른쪽으로 이동 -> 탐색 범위 중 가장 높은 값이 high보다 작다.
while low < toLeft and high > toRight:
# 더 높은 높이를 가진 히스토그램 쪽으로 탐색하여 넓이를 구하고
# 높이는 더 낮은 높이로 갱신한다.
if histogram[toLeft - 1] < histogram[toRight + 1]:
toRight += 1
height = min(height, histogram[toRight])
else:
toLeft -= 1
height = min(height, histogram[toLeft])
maxArea = max(maxArea, height * (toRight - toLeft + 1))
# 한쪽 구간을 다 탐색하지 못한 경우
# 왼쪽 구간이 남음
while low < toLeft:
toLeft -= 1
height = min(height, histogram[toLeft])
maxArea = max(maxArea, height * (toRight - toLeft + 1))
# 오른쪽 구간이 남음
while high > toRight:
toRight += 1
height = min(height, histogram[toRight])
maxArea = max(maxArea, height * (toRight - toLeft + 1))
return maxArea스택
앞에서 풀이한 탑 문제는 새로운 값을 만날 때마다, 앞에 저장해둔 값과 비교하여 집어넣었다.
문제에서 더 낮은 height를 만날 때마다 낮은 쪽으로 갱신해줬다. 그럼 현재 높이가 최대 높이가 되는 것이다.
- 스택의 꼭대기가 가리키는 높이보다 큰 것이 들어온다면 -> push
- 스택의 꼭대기가 가리키는 높이보다 낮은 것이 들어온다면 -> stack의 원소들을 pop하면서 넓이를 구한다.
이때 스택에 저장하는 값은 index이다. 탑에 대한 정보는 별도의 배열로 관리하고 있기때문에 index로 해당하는 값을 찾으면 된다.
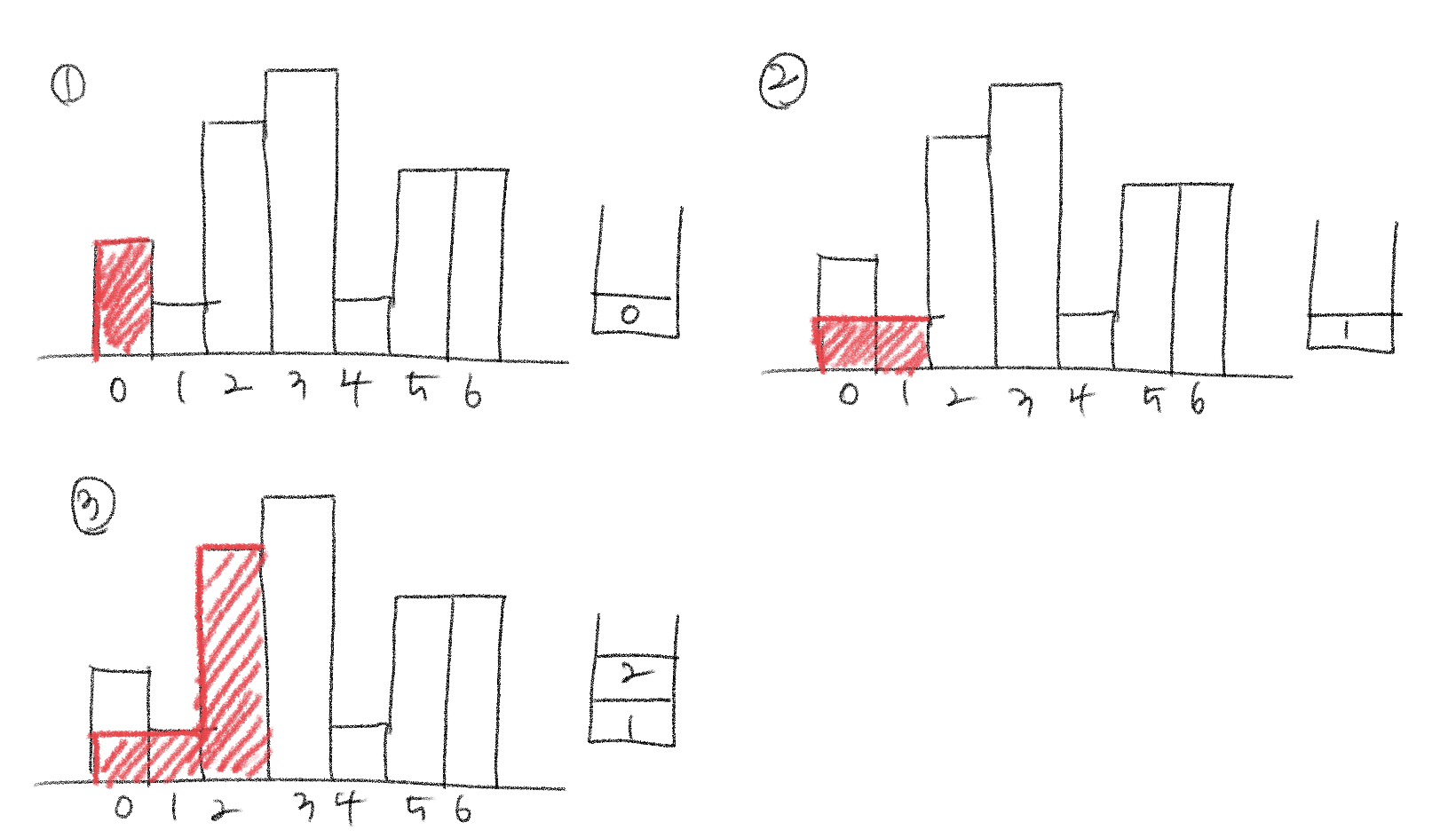
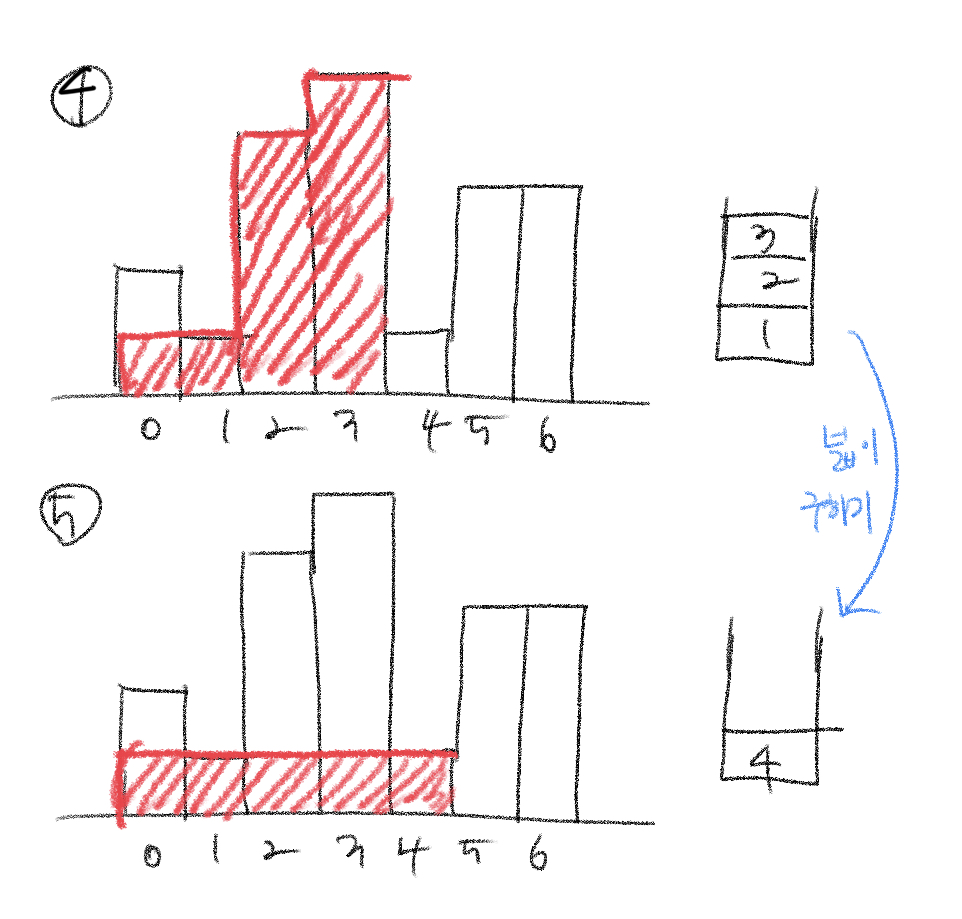
넓이는 어떻게 구할까?
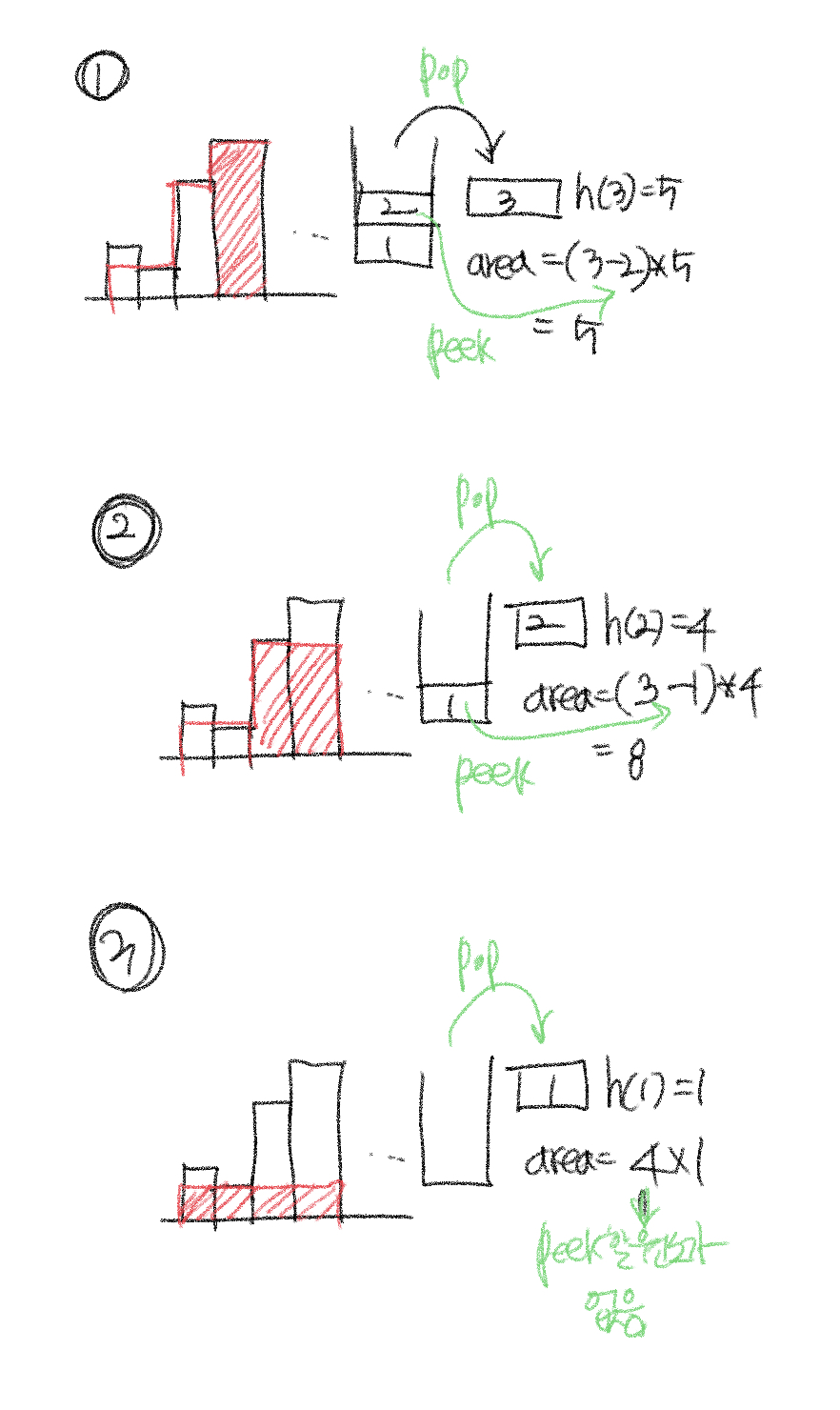
- stack의 맨 위에 있는 원소를 pop하고 높이를 구한다. 직전에 저장된 stack을 peek하여 index를 확인한다.
(현재 index값 -peek한 값) * 높이로 넓이를 구한다. - 1과 마찬가지이다.
- peek할 stack 원소가 더 이상 없다면 3번째에서 4번째 인덱스로 갈 때 발생한 일이기 때문에
4 * 현재 높이를 계산하여 넓이를 구한다.
이런식으로 면적을 계속 계산하여 maxArea를 갱신하는 방식이다.
코드
분할 정복
import sys
from sys import stdin as s
s = open("input.txt", "rt")
def getMidArea(low, high, mid):
toLeft = mid
toRight = mid
height = histogram[mid] # 높이를 구한다.
maxArea = height # 폭이 1이므로 넓이가 높이 = 면적이 된다.
# toLeft는 low 밖이 영역 밖이므로
# toRight는 right 안으로
while low < toLeft and high > toRight:
# 높은 값을 선택한다.
# height는 기존보다 작거나 같에 갱신한다.
# 오른쪽이 더 크므로 오른쪽으로 이동한다.
if histogram[toLeft - 1] < histogram[toRight + 1]:
toRight += 1
height = min(height, histogram[toRight])
# 왼쪽이 더 크므로 왼쪽으로 이동한다.
else:
toLeft -= 1
height = min(height, histogram[toLeft])
maxArea = max(maxArea, height * (toRight - toLeft + 1))
# 왼쪽 구간을 탐색하지 못한 경우
while low < toLeft:
toLeft -= 1
height = min(height, histogram[toLeft])
maxArea = max(maxArea, height * (toRight - toLeft + 1))
# 오른쪽 구간을 다 탐색하지 못한 경우
while high > toRight:
toRight += 1
height = min(height, histogram[toRight])
maxArea = max(maxArea, height * (toRight - toLeft + 1))
return maxArea
def getArea(low, high):
# 막대 폭(넓이)이 1일 경우, 높이가 넓이가 된다.
if low == high:
return histogram[low]
# 1. 가운데 위치를 구한다.
mid = (low + high) // 2
# 2. 가운데 위치 기준으로 나눠서 큰 것을 저장한다.
leftArea = getArea(low, mid)
rightArea = getArea(mid + 1, high)
# 3. leftArea와 rightArea 중 큰 것을 구한다.
maxArea = max(leftArea, rightArea)
# 4. 구간의 최대 넓이를 구한다.
maxArea = max(getMidArea(low, high, mid), maxArea)
return maxArea
while True:
histogram = list(map(int, s.readline().split()))
if histogram[0] == 0:
break
n = histogram.pop(0)
print(getArea(0, len(histogram) - 1))스택
import sys
from sys import stdin as s
s = open("input.txt", "rt")
def getArea(histogram, n):
stack = []
maxArea = 0
for i in range(n):
'''
이전 막대보다 현재 히스토그램 높이가 작으면
자신보다 작거나 같은 것들은 모두 pop하여 최대 넓이는 구한다.
'''
while (len(stack) != 0 and histogram[stack[-1]] > histogram[i]):
height = histogram[stack.pop()] # 이전 체인의 높이
# pop하고 이전 체인이 없어 비어있다면 0번째 index부터 (i-1)번째 인덱스까지 유일한 폭이 된다.
if len(stack) == 0:
width = i
# 비어있지 않다면, 더 작은 높이를 가진 체인이 있다는 것이다.
else:
width = i - 1 - stack[-1]
maxArea = max(maxArea, height * width) # 최대 넓이 갱신
'''
i보다 작거나 같은 것이므로 넣어준다.
'''
stack.append(i)
while len(stack) != 0:
height = histogram[stack.pop()]
if len(stack) == 0:
width = n
else:
width = n - stack[-1] - 1
maxArea = max(maxArea, width * height)
return maxArea
while True:
case = list(map(int, s.readline().split()))
n = case.pop(0)
if n == 0:
break
print(getArea(case, n))Reference

