그리디 알고리즘이란?
그리디 알고리즘은 눈 앞의 이익을 우선 추구하는 알고리즘을 말한다.
do {
가장 좋아 보이는 선택
} until (해 구성 완료)그리디 알고리즘 예시로는 최소 신장 트리를 찾는 프림 알고리즘이있다.
프림 알고리즘은 집합 S를 공집합에서 시작하여 모든 정점을 포함할 때까지 키워나간다. 이 과정에서 간선을 선택할 때 눈 앞에 이득을 바라보면 그리디 알고리즘에 속한다.
아래 그림처럼 프림 알고리즘은 정점의 연결 비용을 최소 비용으로 갱신하면서 업데이트하는 것을 확인할 수 있다.
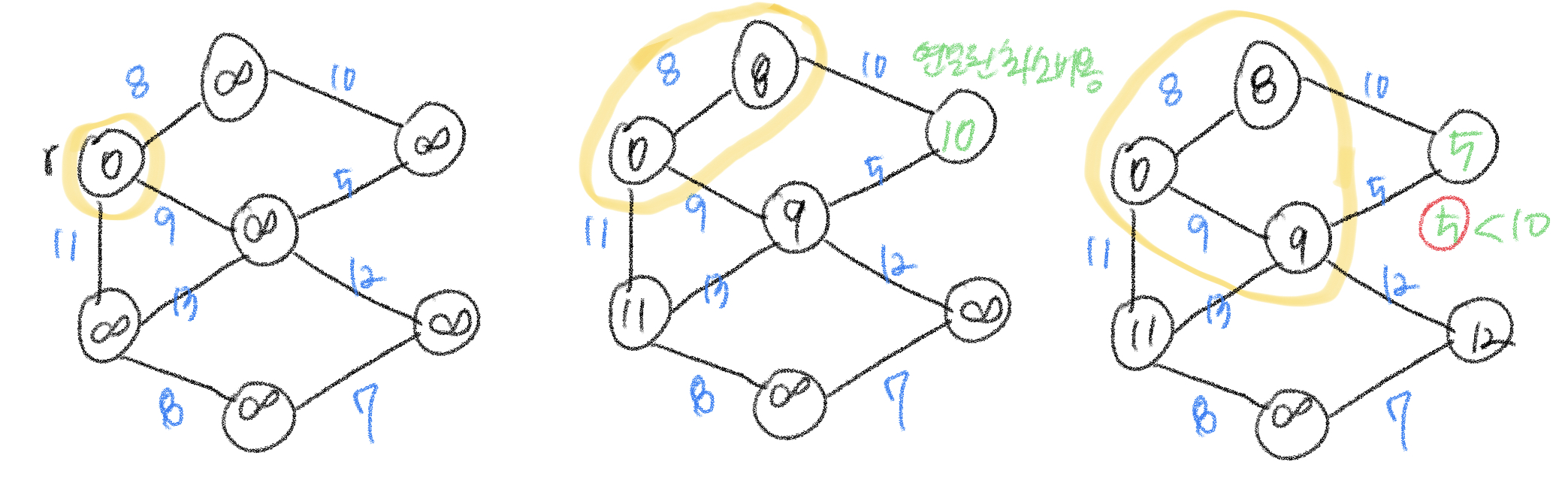
Prim(G, r) # G:그래프, r: 시작 정점
{
s <- ∅; T <- ∅; # S: 정점 집합, T: 간선 집합
정점 r을 집합 S에 더한다.
while (S != V) {
S에서 V-S를 연결하는 간선들 중 최소 길이의 간선 (x, y)를 찾는다.
T에 간선 (x, y)를 더한다.
정점 y를 집합 S에 더한다.
}
}최소 신장 트리는 간선의 합을 최소로 하는 신장 트리를 찾는 것이다. 즉 부분적으로 만들 수 있는 시장 트리에 연결할 수 있는 간선 중 길이가 가장 짧은 것을 택하는 것이다.
그리디 알고리즘으로 최적해가 보장되지 않는 예
P12865 평범한 배낭
유명한 배낭 문제를 살펴보자.
배낭 문제는 배낭에 담을 수 있는 최대 무게가 한정되어 있을 때, 가치와 무게가 있는 짐을 넣으면서 가치의 합이 최대가 되는 방법을 찾는 문제이다.
배낭 문제는 크게 다음으로 구분된다.
- 분할가능 배낭문제(Fractional Knapsack Problem): 담을 수 있는 물건이 나누어 질 때(설탕 g)
- 0-1 배낭 문제(0-1Knapsack Problem): 담을 수 있는 물건이 나누어질 수 없을 때(담는다, 안담는다)
이 문제는 배낭의 물건들이 나뉘지 않기 때문에 분할가능 배낭 문제에 해당된다.
from sys import stdin as s
import sys
n, k = map(int, s.readline().split()) # 물품 수, 준서가 버틸 수 있는 무게
backpack = [[0 for _ in range(k+1)] for _ in range(n+1)]
stuff = [[0, 0]]
for i in range(n):
stuff.append(list(map(int, s.readline().split())))
for i in range(1, n+1): # -> 물건의 무게
for j in range(1, k+1): # -> 가방의 무게
weight = stuff[i][0] # 무게
value = stuff[i][1] # 가치
if j < weight:
backpack[i][j] = backpack[i-1][j]
else:
backpack[i][j] = max(value + backpack[i-1][j-weight], backpack[i-1][j])
print(backpack[n][k])이 문제의 DP 2차원 배열은 다음과 같이 정의된다.
DP[i][j]: 처음부터 i번째까지 물건들을 살펴보고, 배낭 용량이 j일 때 배낭에 들어간 물건들의 가치 합 최댓값- DP 배열의 점화식: DP[i][j] = max(DP[i-1][j], DP[i-1]j-weight[i]] + value[i]) 다음을 비교한다.
- 배낭 용량이 j일 때, 배낭에 들어간 물건들의 가치의 합의 최댓값
- 처음부터 i-1번째까지의 물건을 살펴보고, i번째 물건을 배낭에 넣었을 때 가치의 합
이 문제를 그리디 방식으로 푼다면 어떨까?
물건들을 가치 순서로 정렬하여 가장 큰 가치를 갖는 물건부터 배낭에 넣을 것이다. 이 경우 원하는 최댓값을 얻을 수 없다.
만약 이 문제가 담을 수 있는 물건의 무게를 단위 무게로 환산할 수 있다면(= 자를 수 있다면), 단위 부피당 가치가 큰 물건부터 넣다가 물건을 넣을 때 보따리 용량을 초과하면 남은 용량에 들어갈 만큼만 잘라서 넣으면 된다.
그리디 알고리즘으로 최적해가 보장되는 예
P1931: 회의실 배정
회의실 배정 문제는 여러 부서에서 회의실을 사용하므로 미리 신청 받아 스케쥴링하는 문제이다. 이때 가장 많은 수의 회의를 소화할 수 있어야 한다.
예를들어, 시작시간과 종료시간으로 이루어진 다음 일정이 있다고 하자.
- (1, 4), (3, 5), (0, 6), (5, 7), (3, 8), (5, 9), (6, 10), (8, 11), (8, 12), (2, 13), (12, 14)
그리디한 선택을 하자면 종료시간이 가장 빠른 일정을 선택하여 최적해를 구할 것이다.
회의가 최대한 빨리 끝내야 다른 회의를 진행할 수 있기 때문이다.
from sys import stdin as s
import sys
n = int(s.readline())
meeting = []
for i in range(n):
start, finish = map(int, s.readline().split())
meeting.append([start, finish])
meeting.sort(key=lambda meeting: (meeting[1], meeting[0]))
def greedySchedule():
count = 1
last = meeting[0][1]
for m in range(1, n):
if meeting[m][0] >= last:
count += 1
last = meeting[m][1]
return count
print(greedySchedule())그리디 알고리즘과 동적 프로그래밍
그리디 알고리즘은 동적 프로그래밍과 다르게 단계마다 선택을 하고 선택된 해가 부분 문제의 해가 된다.
동적 프로그래밍에서 부분 문제를 풀고 전체 문제를 풀이했다면, 그리디 알고리즘은 부분 문제를 풀이하기 전에 전체 문제를 푼다.
책에는 이렇게 나와있지만 사실 잘 모르겠다.
배낭 문제의 경우에도 본인은 무게를 정렬하여 그리디 방식으로 풀려고 하였으나, 반례가 나왔다.
찾아보니 비슷한 고민을 하는 사람들이 많다.
만약 동적 계획법 문제를 그리디로 풀다가 틀렸다면, 그것은 그리디 방식이 잘못되었다는 것이다. 하지만 풀이가 그리디인데 동적 계획법으로 풀이하는 것은 복잡도 측면에서 문제가 될 것이다.
즉 많이 풀면서 직관과 경험을 기르는 것이 중요하다.
Reference
- 쉽게 배우는 알고리즘
- Introduction to algorithms

