
우선순위 큐(Priority Queue)
일반적인 큐는 선입선출(FIFO) 구조로 먼저 들어온 데이터가 처리된다.
우선순위 큐는 데이터 추가는 어떤 순서로 해도 상관없지만, 우선 순위가 높은 데이터부터 처리되는 자료구조이다.
- 우선순위 큐를 구현하는 방식은 배열, 연결리스트, 힙으로 구현할 수 있다. 보통
시간복잡도가 낮은 힙(Heap)을 사용한다.
Heap
최솟값, 최댓값을 찾아내는 연산을 빠르게 할 수 있는 완전이진트리 자료구조이다.
- 최소 힙: 루트 노드가 가장 작은 값을 가지고, 항상 부모 노드는 자식 노드보다 작은 값을 갖는다.
- 최대 힙: 루트 노드가 가장 큰 값을 가지고, 항상 부모 노드는 자식 노드보다 큰 값을 갖는다.
힙 정렬하기
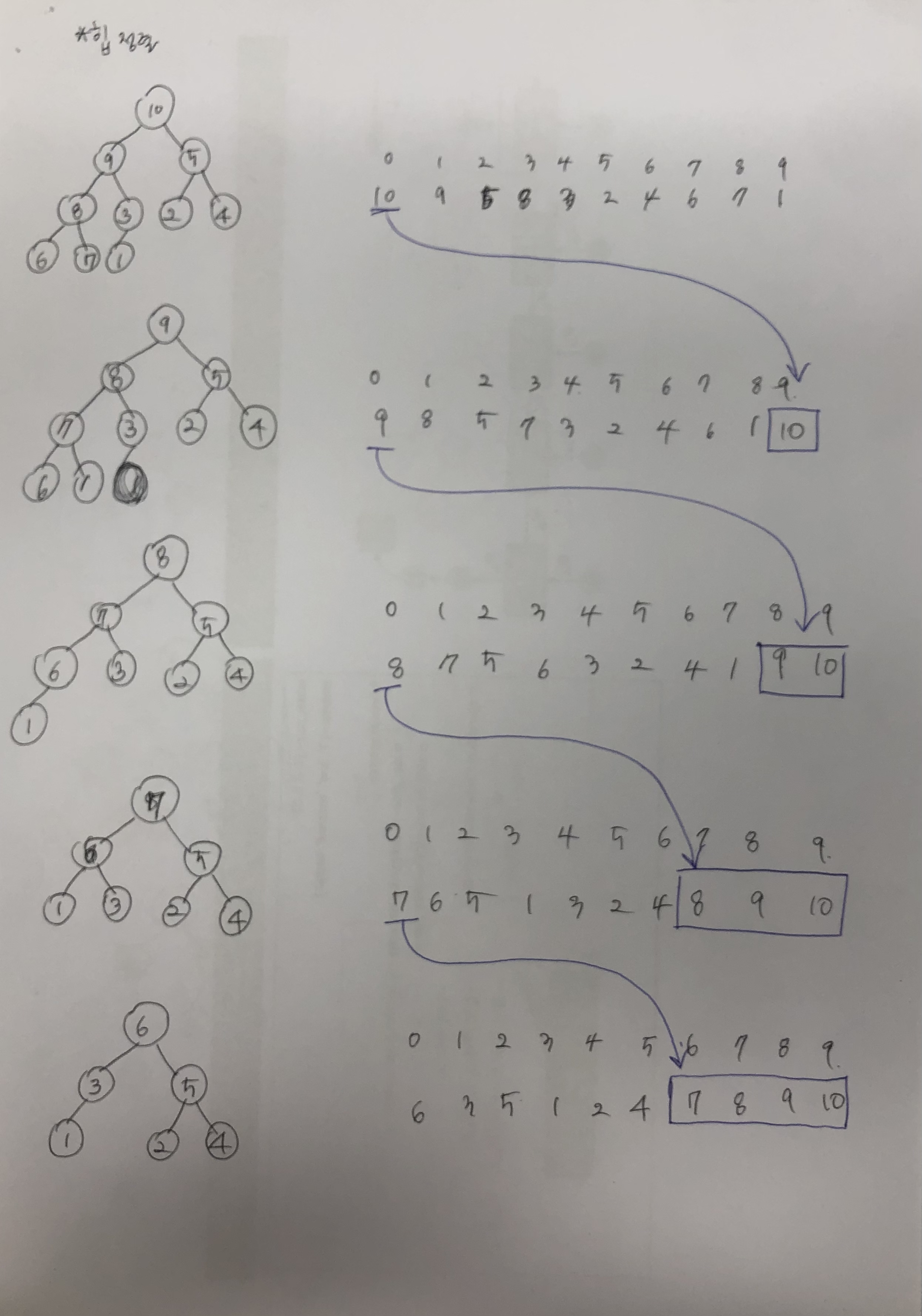
배열을 힙으로 만들기
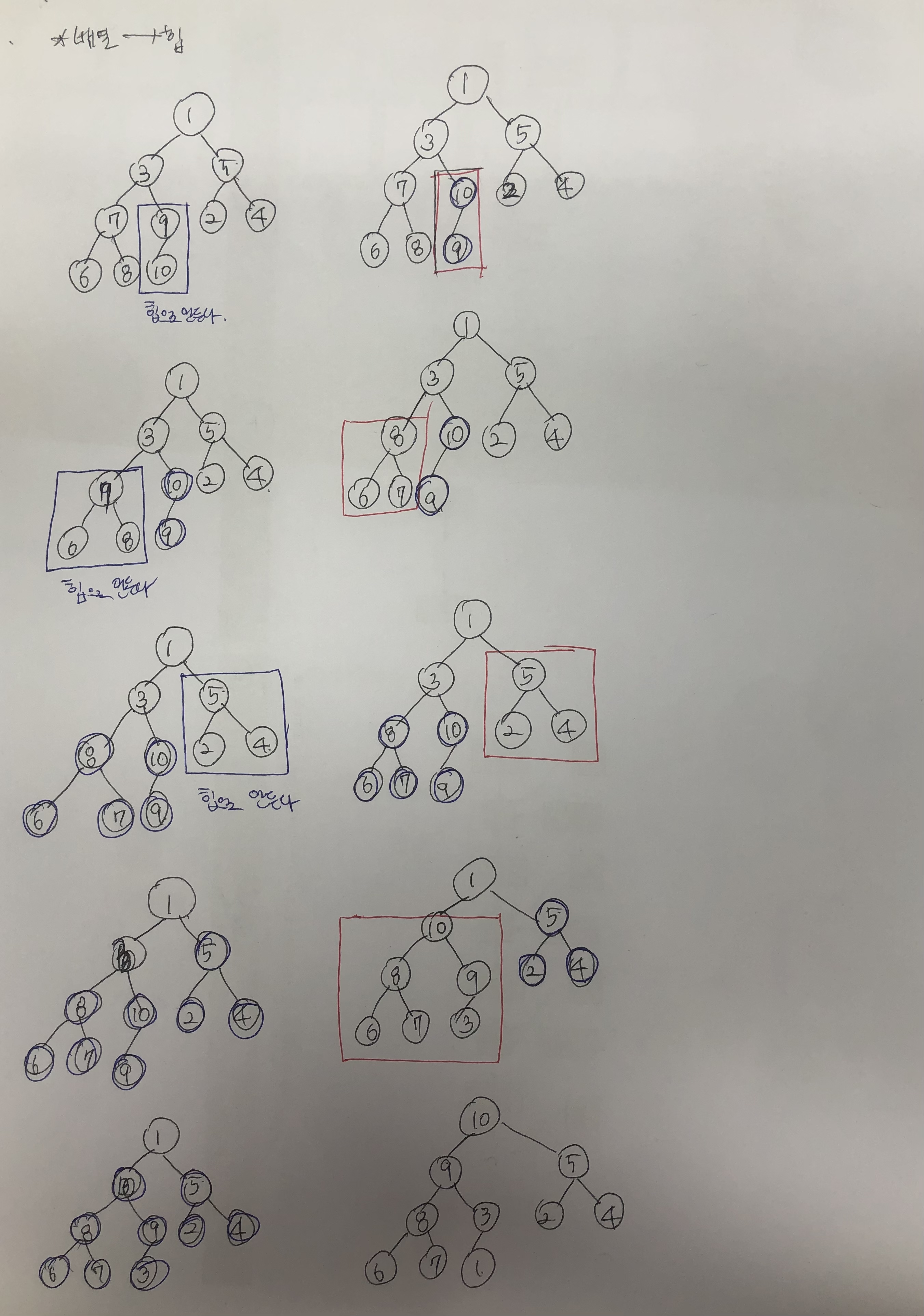
python에서 우선순위 큐 사용하기
# 클래스 임포트
from queue import PriorityQueue
# 생성자를 이용해서 비어있는 우선순위 큐를 초기화한다.
queue = PriorityQueue()
# 우선순위 큐 기본 사이즈는 무한대이다.
# 크기를 지정하면 특정 크기를 가진 우선순위 큐를 생성할 수 있다.
size_queue = PriorityQueue(maxsize=10)
# 원소 추가
queue.put(2)
queue.put(6)
queue.put(10)
queue.put(1)
# 큐에서 원소 삭제 -> 크기 순서대로
print(queue.get()) # 1
print(queue.get()) # 2
print(queue.get()) # 6
print(queue.get()) # 10
# 졍렬 기준 변경 -> (우선순위, 값)의 튜플 형태로 데이터를 추가하고 제거한다.
queue.put((3, 'Apple'))
queue.put((1, 'Banana'))
queue.put((2, 'Cherry'))
print(queue.get()[1]) # Banana
print(queue.get()[1]) # Cherry
print(queue.get()[1]) # Appleheapq 모듈로 힙 자료구조 사용하기
이진트리(binary tree)기반의 최소 힙(min heap) 자료구조를 알아보자.
원소들은 항상 정렬된 상태로 추가, 삭제되며 min heap에서 가장 작은 인덱스가 0으로 이진 트리 루트에 위치한다.
min heap 내의 모든 원수(k)는 항상 자식들 (2k+1, 2k+2)보다 작거나 같도록 원소가 추가되고 삭제된다.( heap[k] <= heap[2*k+1] and heap[k] <= heap[2*k+2])
import heapq
hq = []
print(hq) # []
heapq.heappush(hq, 3)
heapq.heappush(hq, 2)
heapq.heappush(hq, 1)
print(hq) # [1,3,2] min Heap 기준으로 값 추가
# 값 삭제 후 반환한다.
print(heapq.heappop(hq)) # 1
print(heapq.heappop(hq)) # 2
print(heapq.heappop(hq)) # 3
# 기존 리스트를 Min Heap으로 변환한다.
hq = [3, 5, 4, 1, 2]
heapq.heapify(hq)
print(hq) # [1, 2, 4, 5, 3]
# Max Heap 구현 방법1 -> 추가 및 출력에 -를 붙인다.
heapq.heappush(hq, -1)
heapq.heappush(hq, -2)
heapq.heappush(hq, -3)
print(-heapq.heappop(hq)) # 3
print(-heapq.heappop(hq)) # 2
print(-heapq.heappop(hq)) # 1
hq = []
# Max Heap 구현 방법2 -> 튜플을 이용한다.
heapq.heappush(hq, (-1, 1))
heapq.heappush(hq, (-2, 2))
heapq.heappush(hq, (-3, 3))
print(heapq.heappop(hq)[1]) # 3
print(heapq.heappop(hq)[1]) # 2
print(heapq.heappop(hq)[1]) # 1+) PriorityQueu와 heapq 차이가 무엇인지 궁금해졌다. 다른 사람의 블로그에 정리된 글로 확인해보니 Priority Queue는 Heapq로 구현되어 있다. 다만 PrioriyQueue는 Thread-Safe하고 heapq는 Non-safe하다.(Thread-safe와 Non-safe가 무슨 뜻인지는 더 알아보는 것으로...) 이런 이유로 PriorityQueue는 Thread-safe한지 확인해야해서 시간이 더 느리다.
문제로 살펴보기
P11279: 최대 힙
from heapq import heappop, heappush
from sys import stdin as s
import heapq
N = int(s.readline())
heap = []
for i in range(N):
number = int(s.readline())
if number == 0:
if len(heap) == 0:
print("0")
else:
# heappop: heap에서 꺼내고 튜플 형태로 되어있으니 value만 꺼내온다.
print(heappop(heap)[1])
else:
# maxheap은 튜플로 (-number, number) 형태로 넣을 수 있다.
heappush(heap, (-number, number))P1927: 최소 힙
from heapq import heappop, heappush
from sys import stdin as s
s = open("input.txt", "rt")
N = int(s.readline())
heap = []
for i in range(N):
number = int(s.readline())
if number == 0:
if len(heap) == 0:
print("0")
else:
# tuple로 저장했으니까 value만 꺼내온다.
print(heappop(heap)[1])
# print(heappop(heap))
else:
# heap에 데이터를 추가하면 최소힙이 만들어진다.
heappush(heap, (number, number))
# heappush(heap, number)P1655. 가운데를 말해요
처음에 생각한 방식은 매번 들어올 때마다 정렬을 힙 정렬을 해주고 가운데 값을 찾는 것이었는데 데이터가 제대로 추가되지 않았다.
풀이 방식은 두 개의 Heap을 만들어서, leftHeap과 rightHeap에 번갈아 원소를 넣어준다. leftHeap은 오름차순으로 rightHeap은 내림차순으로 정렬하여 각자의 맨 위에서 꺼내온 원소를 가지고 중앙값을 찾는다.
from heapq import heappop, heappush
from sys import stdin as s
s = open("input.txt", "rt")
# 백준이가 외치는 정수의 개수
N = int(s.readline())
# 오름차순으로 정렬
leftHeap = []
# 내림차순으로 정렬
rightHeap = []
for i in range(N):
number = int(s.readline())
# leftHeap과 rightHeap에 번갈아 넣어주면서 균형을 맞춘다.
if len(leftHeap) == len(rightHeap):
# 최대힙으로 구성 -> 오름차순(맨 위에 있는 것을 꺼내면 가장 큰 값)
heappush(leftHeap, -number)
else:
# 최소힙으로 구성 -> 내림차순(맨 위에 있는 것을 꺼내면 가장 작은 값)
heappush(rightHeap, number)
# rightHeap은 leftHeap보다 작게 맞춰주기 위해서 균형이 맞지 않으면 수정해준다.
if rightHeap and rightHeap[0] < -leftHeap[0]:
leftValue = heappop(leftHeap)
rightValue = heappop(rightHeap)
# 값 비교 후 교체하여 왼쪽은 중간값보다 작은 값
# 오른쪽은 중간값보다 큰 값이 들어가도록 한다.
heappush(leftHeap, -rightValue)
heappush(rightHeap, -leftValue)
# 왼쪽부터 먼저 넣기 시작하고, (홀수이면 자동으로 가운데에 있는 원소가 나옴)
# 외친 수의 개수가 짝수개라면 중간에 있는 두 수 중 작은 수를 말한다.
print(-leftHeap[0])P1715. 카드 정렬
문제의 목표인 카드 비교 횟수를 최소한으로 만들려면 정렬된 상태가 되어야 하고, 이전 것을 꺼내서 다시 더하면서 업데이트하는 방식이 되어야 한다.
from heapq import heappop, heappush
from sys import stdin as s
s = open("input.txt", "rt")
N = int(s.readline())
heap = []
result = 0
for i in range(N):
number = int(s.readline())
heappush(heap, number)
if N == 1:
print(0)
else:
while len(heap) > 1:
# 더한 것을 가지고 이어서 또 계산하기 때문에, result와 이전 것을 꺼내서 다시 더한다.
add = heappop(heap) + heappop(heap)
result += add
heappush(heap, add)
print(result)Reference
