BOJ - 15723

백준 문제 링크
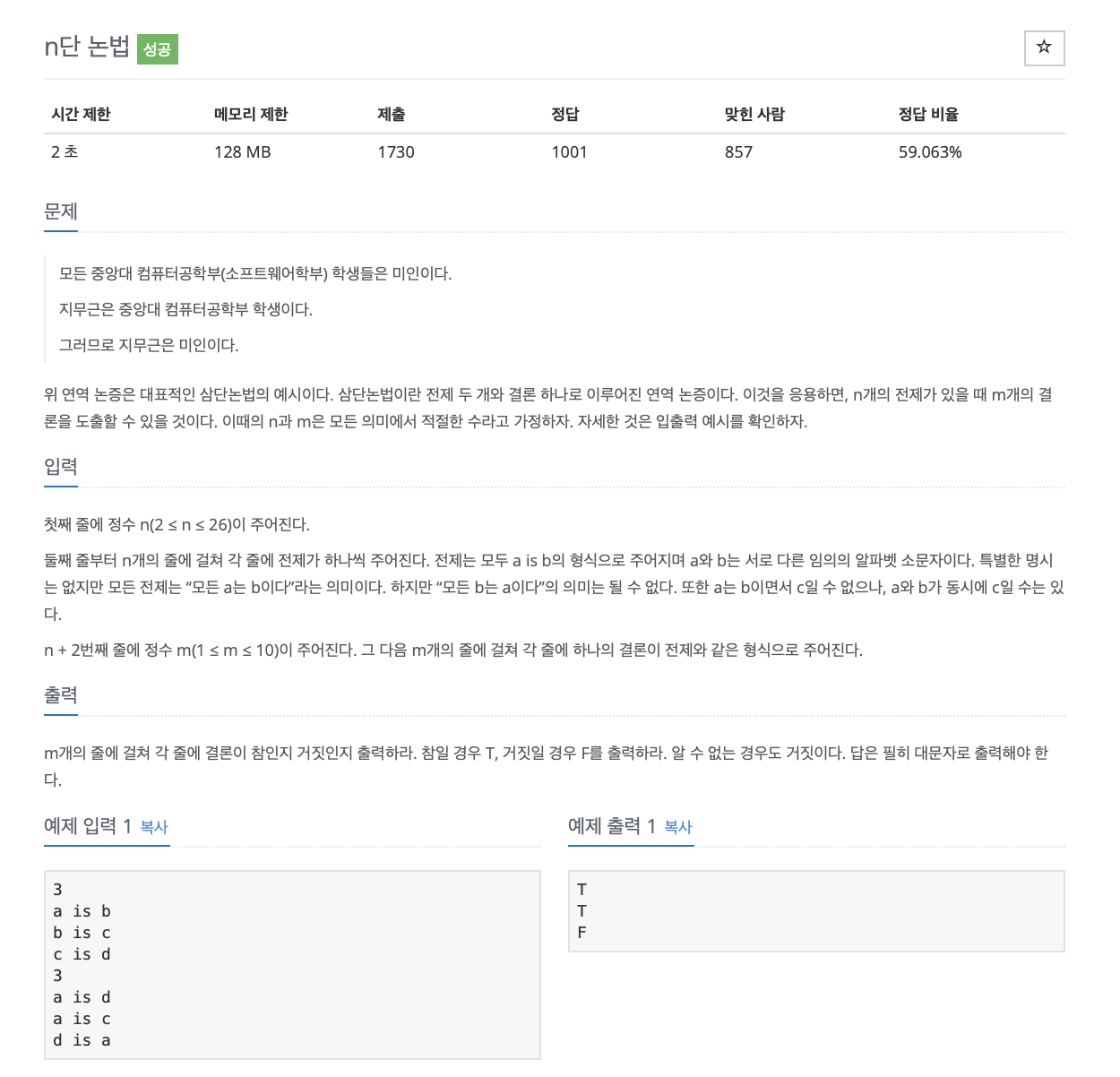
n단 논법

❓접근법

1. n이 작아서 플로이드 워셜 알고리즘을 활용했다.
2. 초기값 INF = int(1e9)로 설정하고, 알파벳이 26개 이므로
   2차원 리스트 graph = [[INF] * 27 for _ in range(27)]로
   만들어 주었다.
3. 플로이드 워셜에서는 자기 자신에서 자기 자신으로 가는 비용은 0이므로, a == b일 때 graph[a][b] = 0으로 만들어 주었다.
4. 나는 알파벳에 해당하는 인덱스를 딕셔너리 형태로 만들었다.
   { 'a' = 1, 'b' = 2, .... ,'z' = 26 }
   n번의 반복문을 통해 graph에서 해당하는 알파벳의 인덱스에
   전제를 삽입했다.
   ex ) a is b 일 때 graph[1][2] = 1
5. 핵심인 3중 반복문을 이용하여, 최단 거리 테이블을 갱신했다.
6. 마지막으로 m번의 반복문을 통해 전제를 받아와서,
   해당하는 전제의 값이 INF이면 'F'를, 아니면 'T'를 출력하면 끝!

👌🏻코드

# 플로이드 워셜 방법 사용

n = int(input())

INF = int(1e9)

graph = [[INF] * (27) for _ in range(27)]

alpha = {'a' : 1, 'b' : 2, 'c' : 3, 'd' : 4, 'e' : 5, 'f' : 6, 'g' : 7,
            'h' : 8, 'i' : 9, 'j' : 10, 'k' : 11, 'l' : 12, 'm' : 13, 
            'n' : 14, 'o' : 15, 'p' : 16, 'q' : 17, 'r' : 18, 's' : 19,
            't' : 20, 'u' : 21, 'v' : 22, 'w' : 23, 'x' : 24, 'y' : 25, 'z' : 26}

for a in range(1, n+1):
    
    for b in range(1, n+1):
        
        if a == b:
            graph[a][b] = 0
            
for _ in range(n):
    
    x, y, z = input().split()
    
    graph[alpha[x]][alpha[z]] = 1


for k in range(1, 27):
    for a in range(1, 27):
        for b in range(1, 27):
            
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
        
        
m = int(input())

for _ in range(m):
    
    x, y, z = input().split()
    
    if graph[alpha[x]][alpha[z]] != INF:
        print('T')
        
    else:
        print('F')