BOJ - 1647

백준 문제 링크
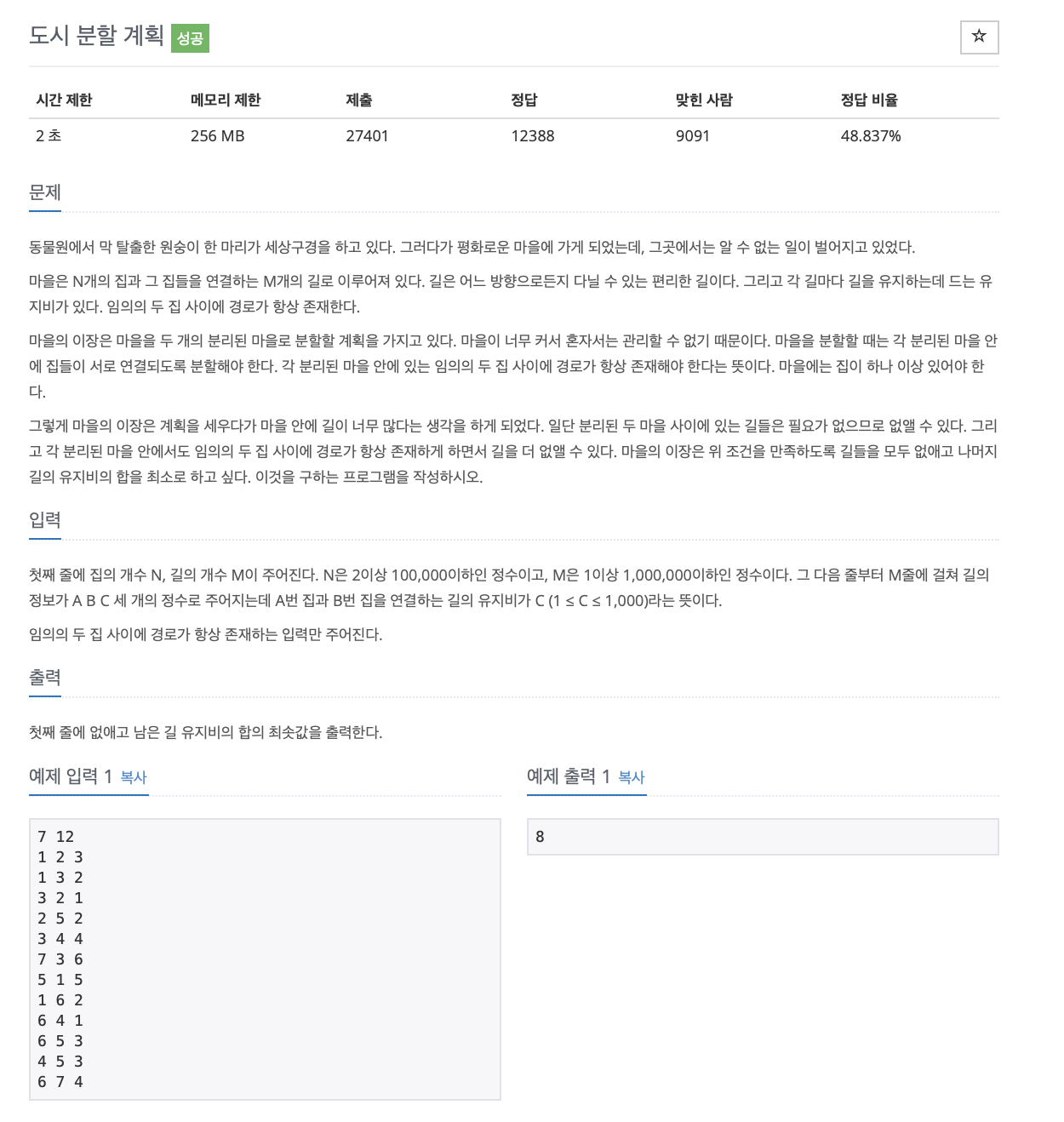
도시 분할 계획

❓접근법

1. 크루스칼 알고리즘을 활용했다.
2. 문제를 해석해보면,
   최소 신장 트리를 최소한의 비용으로 2개의 신장 트리로 분리하는 방법을 묻고 있는데, 최소 신장 트리에서 가장 비싼 간선을 찾아서 제거하면 된다.
3. 먼저 find_parent, union_parent 함수를 만든다.
   간선을 저장할 edges, 총 비용 변수 result,
   가장 비싼 간선 largest_cost 를 만든다.
4. 이제 크루스칼 알고리즘을 전개해서,
   사이클이 발생하지 않는 경우에만 집합에 포함시킨 후
   largest_cost = cost로 지정해준다.
5. 마지막으로 result - largest_cost 를 출력하면 끝!

👌🏻코드

def find_parent(parent, x):
    if parent[x] != x:
        return find_parent(parent, parent[x])
    
    return parent[x]

def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)   
    
    if a < b:
        parent[b] = a
    else:
        parent[a] = b
        
n, m = map(int, input().split())

parent = [i for i in range(n + 1)]

edges = []
result = 0
largest_cost = 0 # 최소 신장트리에 포함되는 간선 중 가장 비용이 큰 간선

for _ in range(m):
    a, b, cost = map(int, input().split())
    edges.append((cost, a, b))
    
edges.sort()

parent = [i for i in range(n + 1)]

result = 0
largest_cost = 0


for edge in edges:
    cost, a, b = edge
    
    # 사이클이 발생하지 않는 경우에만 집합에 포함시키기
    if find_parent(parent, a) != find_parent(parent, b):
        union_parent(parent, a, b)
        result += cost
        largest_cost = cost
      
print(result - largest_cost)