🌱 이분 그래프란
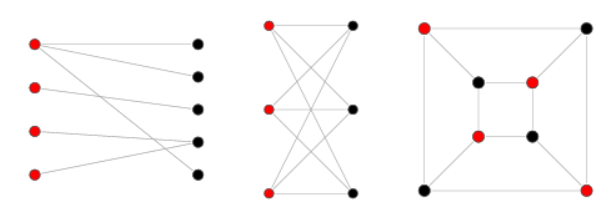
인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프
즉, 그래프의 모든 정점이 두 그룹으로 나눠지고 서로 다른 그룹의 정점이 간선으로 연결되어져 있는 그래프를 이분 그래프라고 한다.
🌱 특징
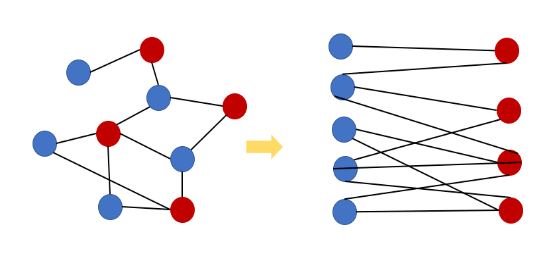
- 이분 그래프인지 확인하는 방법은 BFS, DFS 탐색을 이용하면 된다.
- 이분 그래프는 BFS를 할 때 같은 레벨의 정점끼리는 같은 색이다.
- 연결 성분의 개수(Connected Component)를 구하는 방법과 유사하다.
- 모든 정점을 방문하며 간선을 검사하기 때문에 시간 복잡도는 O(V+E)로 그래프 탐색 알고리즘과 같다.
🌿 이분 그래프 확인 방법
서로 인접한 정점이 같은 색이면 이분 그래프가 아니다.
이분 그래프인지 확인하는 방법은 BFS 또는 DFS를 이용하면 된다.
- BFS, DFS로 탐색하면서 정점을 방문할 때마다 두 가지 색 중 하나를 색칠한다.
- 다음 정점을 방문하면서 자신과 인접한 정점은 자신과 다른 색으로 칠한다.
- 탐색을 진행할 때 자신과 인접한 정점의 색이 자신과 동일하면 이분 그래프가 아니다.
- BFS의 경우 정점을 방문하다가 만약 같은 레벨에서 정점을 다른 색으로 칠해야 한다면 무조건 이분 그래프가 아니다.
- 모든 정점을 방문했는데 위와 같은 경우가 없다면 이분 그래프이다.
- 이 때 주의할 점은 연결 그래프와 비연결 그래프를 둘 다 고려해야한다는 것이다.
- 비연결 그래프인 경우 모든 정점에 대해서 확인하는 작업이 필요하다.
Reference : https://gmlwjd9405.github.io/2018/08/23/algorithm-bipartite-graph.html
