🌱 깊이 우선 탐색(DFS)

---

그래프 완전 탐색 기법 중 하나로, 그래프의 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘이다.

기능	특징	시간 복잡도 (노드 수: V, 에지 수: E)	응용
그래프 완전 탐색	재귀 함수로 구현	O(V+E)	단절점 찾기
.	스택 자료구조 이용	.	단절선 찾기
.	.	.	사이클 찾기
.	.	.	위상 정렬

실제 구현 시 재귀 함수를 이용하므로 스택 오버플로에 유의해야 한다.

핵심 이론

• 노드 방문 여부를 체크할 배열이 필요
• 그래프는 인접 리스트로 표현
• DFS의 탐색 방식은 후입선출(LIFO) 특성을 가지므로 Stack을 사용

🌿 알고리즘

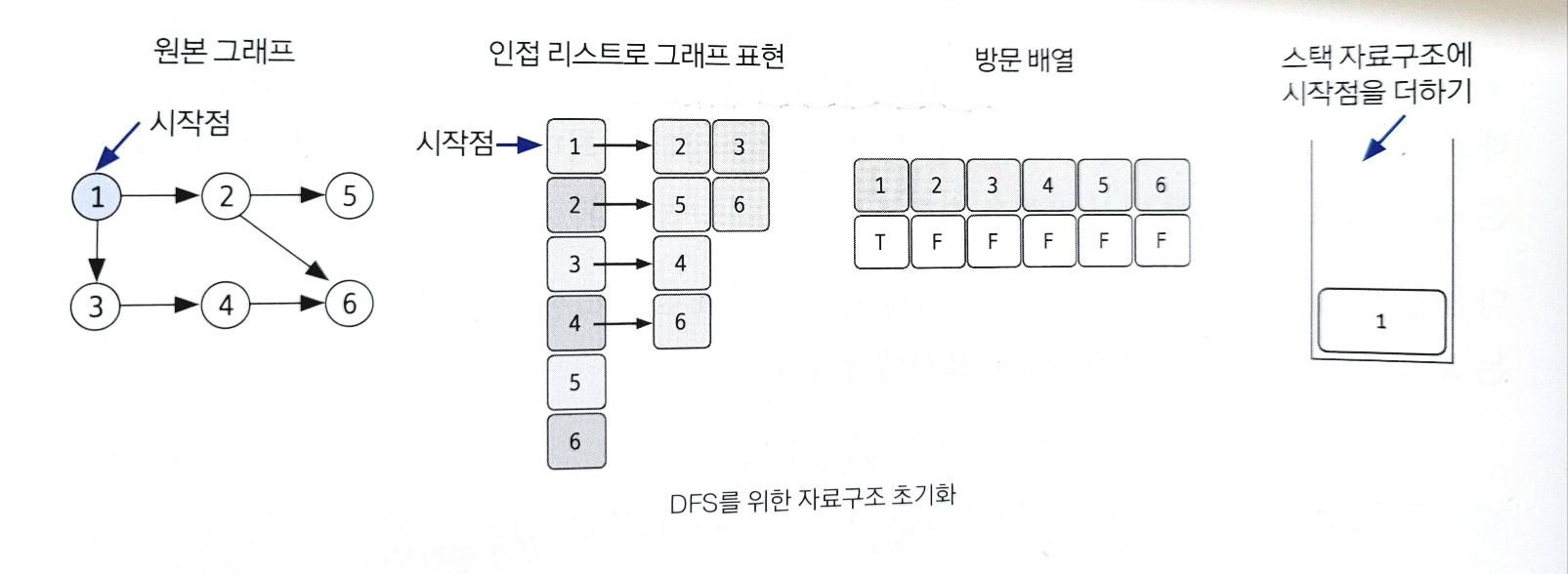
1. DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기

DFS를 위해 필요한 초기 작업은 인접 리스트로 그래프 표현하기, 방문 배열 초기화하기, 시작 노드 스택에 삽입하기이다.

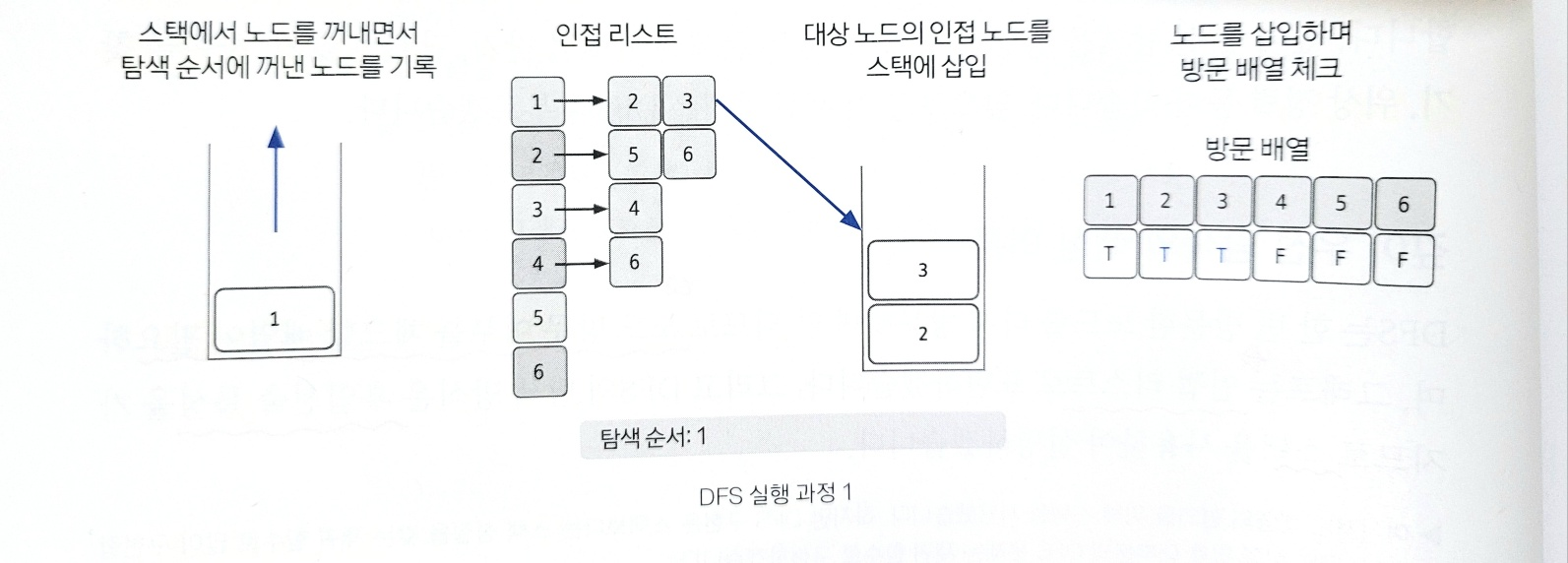
2. 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입하기

pop을 수행하여 노드를 꺼낸다. 꺼낸 노드를 탐색 순서에 기입하고 인접 리스트의 인접 노드를 스택에 삽입하며 방문 배열을 체크한다.

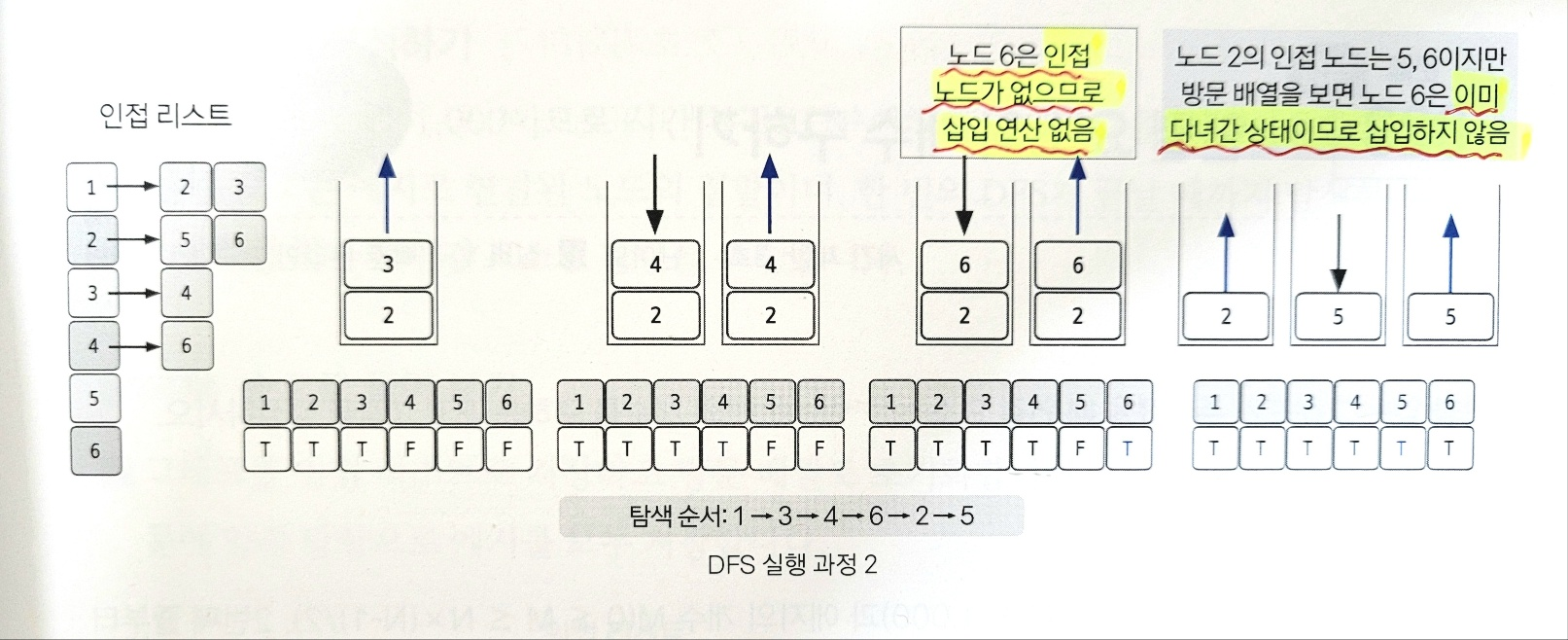
3. 스택 자료구조에 값이 없을 때까지 반복하기

이미 다녀간 노드는 방문 배열을 바탕으로 재삽입하지 않는 것이 핵심이다.

🌿 구현

import java.io.IOException;
import java.util.*;

public class Main {

    private static ArrayList<Integer>[] A;
    private static boolean[] visited;

    public static void main(String[] args) throws IOException {
        int N = readInt(); //노드 개수
        int M = readInt(); //간선 개수

        A = new ArrayList[N + 1]; //인접 리스트
        visited = new boolean[N + 1]; //밤문 여부

        //노드마다 연결리스트 달기
        for (int i = 1; i <= N; i++) {
            A[i] = new ArrayList<>();
        }

        for (int i = 0; i < M; i++) {
            int s = readInt();
            int e = readInt();
            A[s].add(e); //무방향 -> 양방향 에지 저장
            A[e].add(s);
        }

        for (int i = 1; i <= N; i++) {
            if (!visited[i]) {
                DFS(i);
            }
        }

        System.out.println(cnt);
    }

    private static void DFS(int v) {
        if (visited[v]) return;

        visited[v] = true;

        for (int i : A[v]) {
            if (!visited[i]) DFS(i);
        }
    }

    static int readInt() throws IOException {
        int c, n = System.in.read() & 15;
        while ((c = System.in.read()) > 32) n = (n << 3) + (n << 1) + (c & 15);
        return n;
    }

}

ref : Do It 알고리즘 코딩 테스트 자바편 by 김종관