최소 힙

hodu·2024년 2월 4일
개발 공부알고리즘자료구조
0

✅ 힙이란?

heap은 완전 이진 트리의 일종으로 우선 순위 큐를 위하여 만들어진 자료 구조이다.
힙은 완전히 정렬한 것은 아니지만 반정렬 상태를 유지한다. (느슨한 정렬 상태)

최소 힙 또는 최대 힙을 이용하는데, 최소 힙을 사용하는 경우 값이 낮은 데이터를 먼저 삭제하고, 최대 힙인 경우에는 가장 큰 데이터를 먼저 삭제한다.

힙은 삽입과 삭제에 O(NlogN)의 시간 복잡도를 갖는다.

파이선이나 자바에는 이를 도와주는 함수를 갖고 있지만,
자바스크립트에서는 직접 힙을 구현해야 이를 사용할 수 있다.

✅ 힙의 종류

힙은 2가지로 나뉘는데,

  • 최대 힙(Max Heap): 모든 노드가 자식 노드보다 작거나 같은 값을 가지는 힙이다. 루트 노드는 최소값을 가진다.
  • 최소 힙(Min Heap): 부모 노드의 값이 자식 노드의 값보다 작거나 같은 완전 이진 트리이다.

로 나뉜다.

✅ 이진 트리

이진 트리(Binary Tree)는 계층적 데이터 구조로,
각 노드가 최대 두 개의 자식 노드를 가질 수 있는 특징을 갖고 있다.
각 요소를 노드라고 하며, 최상위 노드를 루트 노드(root node)라고 하거나
자식을 갖지 않는 노드를 리프 노드(leaf node)라고 합니다.

여러 이진 트리 중 힙은 완전 이진 트리(Full Binary Tree)에 속한다.

힙은 부모와 자식간의 아래와 같은 관계를 갖는다.

  • 왼쪽 자식의 index = 부모의 index * 2 + 1
  • 오른쪽 자식의 index = 부모의 index * 2 + 2
  • 부모의 index = Math.floor((자식의 인덱스 - 1)/ 2)

✅ 힙 구현

삽입 연산
Min Heap의 삽입 연산은 다음과 같은 단계로 이루어진다.

  1. 먼저 마지막 노드로 새로운 요소를 삽입한다.

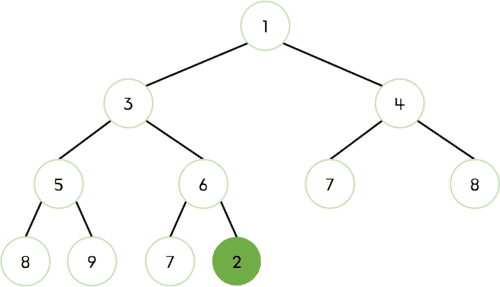
  2. 부모 노드와 비교했을 때 2가 작으므로 교체한다.

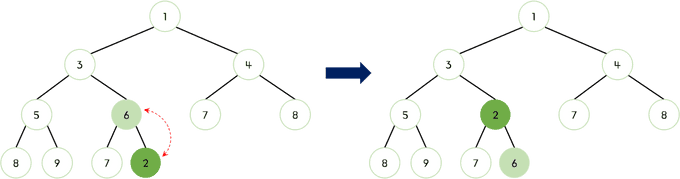
  3. 부모 노드 3과 비교했을 때 2가 작으므로 교체한다.

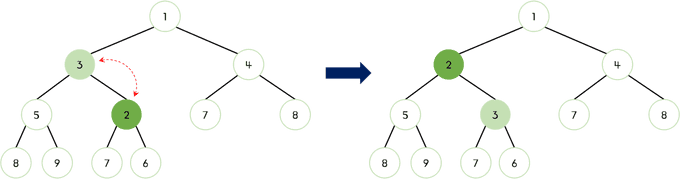
  4. 부모 노드가 더 작으므로 1과 2는 교체하지 않는다.

정리하면

  1. 요소 추가: 힙의 마지막에 새 요소를 추가합니다. 이는 힙을 배열로 구현했을 때, 배열의 끝에 요소를 추가하는 것과 동일합니다.

  2. 위치 교환: 새로 추가된 요소가 힙의 조건을 만족할 때까지 부모 노드와 비교합니다. 최소 힙에서는 새 요소가 부모 노드보다 작을 경우, 두 노드의 위치를 교환합니다.

  3. 재귀적 상향 조정: 새 요소와 부모 노드의 비교 및 교환 과정을 힙의 루트에 도달하거나 더 이상 교환할 필요가 없을 때까지 반복합니다. 이 과정은 힙의 구조적 및 순서적 특성을 유지합니다.

Bubble Up: 힙에 요소를 삽입한 후, 새 요소가 최소 힙 규칙을 만족할 때까지 부모 노드와의 비교 및 교환을 통해 위로 이동하는 과정을 'Bubble Up'이라고 합니다. 이 과정은 새 요소가 적절한 위치에 도달할 때까지 계속되며, 결과적으로 힙은 최소값을 루트 노드에 유지합니다.

class MinHeap {
  constructor() {
    this.heap = [];
  }

  insert(item) {
    this.heap.push(item);
    this.bubbleUp();
  }

  bubbleUp() {
    let index = this.heap.length - 1 //추가한 노드 위치
    let element = this.heap[index]; // 추가한 값 할당

    while (index > 0) { //최상단이 될때까지
      const parentIndex = Math.floor((index - 1) / 2); // 부모 index
      const parent = this.heap[parentIndex]; // 부모 값 할당

      if (parent < element) break; // 부모가 작다면 멈춥니다.

      this.heap[index] = parent; //부모의 값을 자식 index에 할당합니다.
      this.heap[parentIndex] = element; // 자식의 값을 부모 index에 할당합니다.
      index = parentIndex; // 자식 index를 부모 index로 업데이트합니다.
    }
  }

✅ 삭제 연산

Min Heap의 삭제 연산은 다음과 같은 단계로 이루어진다.

  1. 먼저 루트 노드가 삭제된다. 빈 루트 노드 자리에는 힙의 마지막 노드 7을 가져온다.


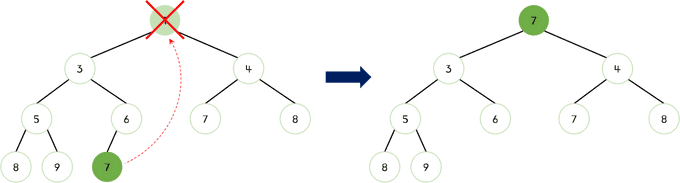
2. 새로운 루트 노드인 7과 자식 노드들(왼쪽, 오른쪽)을 비교했을 때 7이 더 크므로 교체되어야 한다. 이때 자식 노드 중 더 작은 값인 3과 7을 교체한다.

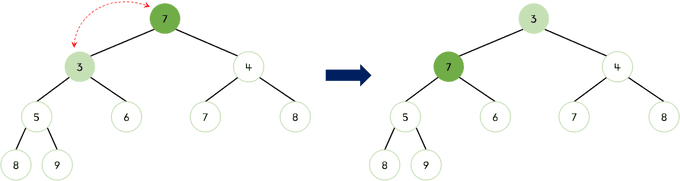
3. 7이 아직 자식 노드들보다 더 크기 때문에 교체해야 한다. 이때 자식 노드 중 더 작은 값인 5와 7이 교체된다. (6보다 5가 더 작기때문에)

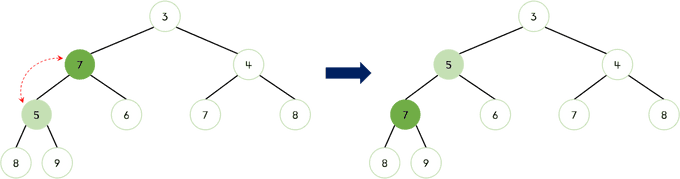
4. 7이 자식 노드들보다 작으므로 더 이상 교체하지 않는다.

정리하면

  1. 루트 노드 제거: 힙에서 가장 작은 값을 가진 노드, 즉 루트 노드를 제거합니다. 이 작업은 힙에서 최소값을 추출하는 과정입니다.

  2. 마지막 노드 이동: 힙의 가장 마지막에 위치한 노드를 루트 노드의 위치로 이동시킵니다. 이는 힙의 구조를 유지하기 위한 조치입니다.

  3. 재배치 과정: 새로운 루트 노드가 자신의 왼쪽과 오른쪽 자식 노드보다 크지 않도록 (최소 힙의 경우) 위치를 조정합니다. 만약 자식 노드 중 하나가 새 루트 노드보다 작다면, 가장 작은 자식 노드와 새 루트 노드의 위치를 교환합니다.

  4. 재귀적 하향 조정: 새 루트 노드를 자식 노드와 비교하고 필요한 경우 위치를 교환하는 과정을 계속 반복합니다. 이 과정은 힙 전체에서 순서적 특성을 만족시킬 때까지 계속됩니다.

Bubble Down: 최소 힙에서 루트 노드를 제거한 후, 마지막 노드를 루트로 이동시키고, 이후 루트 노드가 자신의 자식 노드보다 작거나 같을 때까지 자식 노드와의 교환을 통해 아래로 이동하는 과정을 'Bubble Down'이라고 합니다. 이 과정은 힙의 구조적 및 순서적 특성을 유지하며, 힙에서의 요소 재배치를 효율적으로 수행합니다.

 extractMin() {
    if (this.heap.length === 0) return 0;// 없을 경우에는 0을 출력

    const min = this.heap[0]; // 최소 값
    const last = this.heap.pop(); // 가장 뒤에 있는 노드를 가져온다.
    if (this.heap.length > 0) { // 힙이 남아있다면 진행
      this.heap[0] = last; // 루트 노드에 가장 뒤에 있는 노드 값을 할당한다.
      this.bubbleDown();
    }

    return min;
  }

  bubbleDown() {
    let index = 0
    const element = this.heap[index];// 최상위 노드 값
    const length = this.heap.length; // 길이

    while (true) {
      const leftChildIndex = 2 * index + 1; //왼쪽 자식 노드
      const rightChildIndex = 2 * index + 2; // 오른쪽 자식 노드
      let leftChild, rightChild;
      let swap = null;

      if (leftChildIndex < length) { // 왼쪽 자식의 index가 존재한다면
        leftChild = this.heap[leftChildIndex];
        if (element > leftChild) {
          swap = leftChildIndex;
          // 값이 더 작을 경우 swap에 왼쪽 자식 노드 index 할당
        }
      }

      if (rightChildIndex < length) { // 오른쪽 자식의 index가 존재한다면
        rightChild = this.heap[rightChildIndex];
        if (
          (swap === null && element > rightChild) || 
          (swap !== null && leftChild > rightChild) 
          // 왼쪽 자식의 index가 이미 들어온 경우
        ) {
          swap = rightChildIndex;
          // 오른쪽 자식의 index 할당
        }
      }
      if (swap === null) break; // 부모 노드가 가장 작다면 멈춘다.
      //부모 노드와 가장 작은 노드는 값을 교환하고 index를 자식 노드 index로 업데이트
      this.heap[index] = this.heap[swap]; 
      this.heap[swap] = element;
      index = swap;
    }
  }

✅ 전체 코드


class MinHeap {
  constructor() {
    this.heap = [];
  }

  insert(item) {
    this.heap.push(item);
    this.bubbleUp();
  }

  bubbleUp() {
    let index = this.heap.length - 1 //추가한 노드 위치
    let element = this.heap[index]; // 추가한 값 할당

    while (index > 0) { //최상단이 될때까지
      const parentIndex = Math.floor((index - 1) / 2); // 부모 index
      const parent = this.heap[parentIndex]; // 부모 값 할당

      if (parent < element) break; // 부모가 작다면 멈춥니다.

      this.heap[index] = parent; //부모의 값을 자식 index에 할당합니다.
      this.heap[parentIndex] = element; // 자식의 값을 부모 index에 할당합니다.
      index = parentIndex; // 자식 index를 부모 index로 업데이트합니다.
    }
  }
 extractMin() {
    if (this.heap.length === 0) return 0;// 없을 경우에는 0을 출력

    const min = this.heap[0]; // 최소 값
    const last = this.heap.pop(); // 가장 뒤에 있는 노드를 가져온다.
    if (this.heap.length > 0) { // 힙이 남아있다면 진행
      this.heap[0] = last; // 루트 노드에 가장 뒤에 있는 노드 값을 할당한다.
      this.bubbleDown();
    }

    return min;
  }

  bubbleDown() {
    let index = 0
    const element = this.heap[index];// 최상위 노드 값
    const length = this.heap.length; // 길이

    while (true) {
      const leftChildIndex = 2 * index + 1; //왼쪽 자식 노드
      const rightChildIndex = 2 * index + 2; // 오른쪽 자식 노드
      let leftChild, rightChild;
      let swap = null;

      if (leftChildIndex < length) { // 왼쪽 자식의 index가 존재한다면
        leftChild = this.heap[leftChildIndex];
        if (element > leftChild) {
          swap = leftChildIndex;
          // 값이 더 작을 경우 swap에 왼쪽 자식 노드 index 할당
        }
      }

      if (rightChildIndex < length) { // 오른쪽 자식의 index가 존재한다면
        rightChild = this.heap[rightChildIndex];
        if (
          (swap === null && element > rightChild) || 
          (swap !== null && leftChild > rightChild) 
          // 왼쪽 자식의 index가 이미 들어온 경우
        ) {
          swap = rightChildIndex;
          // 오른쪽 자식의 index 할당
        }
      }
      if (swap === null) break; // 부모 노드가 가장 작다면 멈춘다.
      //부모 노드와 가장 작은 노드는 값을 교환하고 index를 자식 노드 index로 업데이트
      this.heap[index] = this.heap[swap]; 
      this.heap[swap] = element;
      index = swap;
    }
  }
}

🙌 끝으로

최소 힙에 대해서 정리해보았다.
최대 힙도 마찬가지로 작다 -> 크다로 바꿔주면 해결할 수 있는 문제여서 따로 적지 않았다.

최소 힙을 처음 알았을 때, 적잖게 충격을 받았다.
최적화된 알고리즘으로 시간 복잡도를 줄인다는 것은 대단한 아이디어고 발명이다.

프론트엔드 개발자의 길을 걷고 있지만, 알고리즘을 꾸준히해서 알고리즘도 잘알고, 자료 구조에 대해서도 잘 이해하고 싶다.


출처 :
https://chamdom.blog/heap-using-js/

profile
hodu
잘부탁드립니다.
이전 포스트

React의 useCallback 최적화한 커스텀 훅 usePreservedCallback

다음 포스트

modal을 구현하는 2가지 방법 (createPortal, dialog Tag)

0개의 댓글