오늘 문득 적금을 드는데 이율 계산하는 식이 궁금해졌다!
그래서 python으로 만들어서 한번 해보잔 생각이 들었다.
일단 필요한 인자를 생각!
- 원금
- 이율
- 이율 적용 방식
- 기간
위 내개로 계산할 수 있지않을까 생각했다!
내 생각은 반복문으로 12개월간 돌리는 것으로 생각했다!
월 투자금을 P
연 이자율을 r
적용 방식을 n
기간을 t로 정했다
함수로 만들고 계산해보자!
def calculate_savings(P, r, n, t):
total_amount = 0
monthly_interest_rate = r / n
total_periods = t * n
for _ in range(total_periods):
total_amount += P
total_amount *= (1 + monthly_interest_rate)
return total_amount간단하다. P를 기준으로 반복문만 돈다면 두기적으로 계산하는 식에 대해서는 쉽게 할 수 있으니까
P는 항상납입하는 금액이다
그럼 이자 계산은? 이자가 2프로일 경우 0.02인데 이러면 계산 식이 성립이 안되니 1을 더해준다. 그 후 복리 빈도(월별로 할 경우 12겠지?)를 해주면 월별 이자율이 나온다.
이제 납부 기간도 t * n으로 계산해주면 정해진 값이 나온다.
그럼 전체 납부 횟수도 알 수 있으니 그 기간동안 반복문을 돌며 계산하면 된다.
참 쉽죠? 근데 이거 보다 더 쉬운 게 있다!
def calculate_savings2(P, r, n, t):
FV = P * (((1 + r / n) ** (n * t) - 1) / (r / n))
return FV이 식을 보면 필요한 정보가 한줄로 계산되어 있다.
원급을 곱하되, 1+이율을 횟수로 나누고(월 납입이면 12로 나눔) 총 납입 횟수를 제곱해준 후 1을 뺀다. 그 후 다시 이자/횟수로 값을 구한 후 나눠주면 복리 이자가 나온다.
이 식에 대해서는 잘 몰랐는데
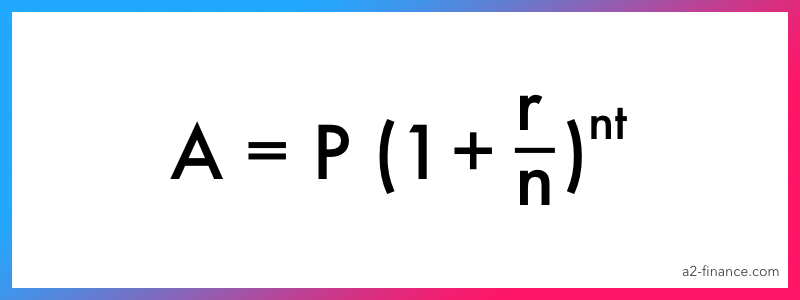
출처 : https://a2-ci.kr/
실제로 유명한 식이었다..
간단하게 계산할 수 있으니 나중에 도움이 될 듯해 작성해보았다.
단리계산은 어렵지않으니.. 뭐.. 필요없겠지..
def calculate_savings2(P, r, n, t):
FV = P * (((1 + r / n) ** (n * t) - 1) / (r / n))
return FV
def calculate_savings(P, r, n, t):
total_amount = 0
monthly_interest_rate = r / n
total_periods = t * n
for _ in range(total_periods):
total_amount += P
total_amount *= (1 + monthly_interest_rate)
return total_amount
P = 1000000 # 월 투자 금액
r = 0.03 # 연 이자율
n = 12 # 연간 복리 빈도
t = 1 # 투자 기간(년)
# 미래 가치 계산
future_value = calculate_savings(P, r, n, t)
# 총 이익 계산
total_investment = P * n * t
total_profit = future_value - total_investment
print(f"만기 시 받게 될 총 금액: {future_value:.2f}원")
print(f"총 이익금: {total_profit:.2f}원")
# # 총 누적 금액 계산
total_accumulated = calculate_savings2(P, r, n, t)
print(f"총 누적 금액: {total_accumulated:.2f}원")
혹시 모르니 전체 코드 넣기
돌려보면 금액이 좀 다르다.
원인에 대해 계속 생각하다가 찾아봤는데 함수에서 적용방식이 매월 투자 후 이자가 즉시 적용되는 시점이라 생각하면 된다
첫번째 코드의 문제점은 매번 동일한 이자가 적용된다 가정되어 상대적으로 부정확한 값이 내려진 것
음.. 둘다 크게 차이는 안나지만 savings가 savings2보다 현실적인 시나리오라고 한다.. 나중에 공부를 더 해봐야겠다
